力扣校招算法通关：双指针技巧全场景拆解 —— 从数组执行到环检测的高效解题范式

文章目录

• 前言
• 双指针
• 例题讲解
• • 移动零 力扣
  • 复写零 力扣
  • 快乐数 力扣
  • 盛最多水的容器 力扣
  • 有效三角形的个数 力扣
  • 查找总价格为目标值的两个商品 力扣
  • 三数之和 力扣

前言

在力扣校招算法题中，双指针技巧是一类高频且实用的解题方法。它并非真正的 “指针”，而是通过两个数组下标（或迭代器）的协同移动，在数组划分、区间求解、环检测等场景中实现高效遍历与逻辑处理，往往能将时间复杂度从暴力法的 O(n平方)优化至O(n)，是校招笔试和面试中突破数组类难题的关键武器。

本专栏将围绕力扣校招高频的双指针题型展开，从 “移动零”“复写零” 的数组操作，到 “快乐数” 的环检测、“盛最多水的容器” 的区间优化，再到 “三数之和” 的多指针协同，逐一拆解双指针的核心逻辑、边界处理与去重技巧，帮助你建立 “看题辨双指针，提笔知如何移” 的解题思维，从容应对校招算法考察中的数组类挑战。

双指针

常用于:数组划分和数组分块

注意:这里的指针不是真的指针，是数组的下标

例题讲解

移动零 力扣

283. 移动零

cur:从左往右遍历数组

dest:已处理区间内，非零元素的最后一个位置

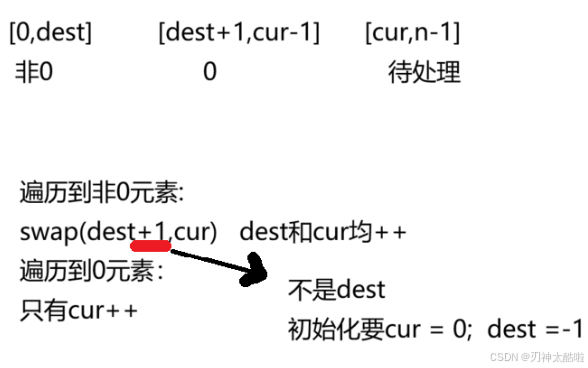
代码展示:
class Solution {
public:
void moveZeroes(vector<int>& nums) {
  int dest = -1;
  int cur = 0;
  for(;cur<nums.size();cur++)
  {
  if(nums[cur] != 0)
  {
  swap(nums[dest+1],nums[cur]);   dest++;
  }
  else{
  ;
  }
  }
  }
  };

复写零 力扣

1089. 复写零

注意:这题要求不要在超过该数组长度的位置写入元素

步骤:

一:先找到最后一个被复写的数

找法:1.先判断cur位置的值(cur放到下标0位置，dest放到下标-1位置)

    2.决定dest向后移动多少步(注意是先移动再判断的)
   3.判断一下dest是否已经到结束位置（等于或超过最后那个数的位置）
 4.cur++

5.如果dest超过最后那个数的位置

让最后那个位置等于0
再cur--;dest-=2

二:从后向前完成复写操作

引申:vector的size()-1就是最后一个位置的下标
区分元素和下标
区分==和=
注意:size()在用来表示下标的时候，建议赋值给int类型的之后再用
不然 eg:dest

代码展示:
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
  int cur = 0; int dest = -1;
  for(;dest<(int)arr.size()-1;cur++)
  {
  if(arr[cur]==0)    dest++;
  dest++;
  }
  cur--;
  if(dest == arr.size())
  {
  arr[arr.size()-1] = 0;
  dest-=2;
  cur--;
  }
  for(;cur>=0;cur--)
  {
  arr[dest] = arr[cur];
  if(arr[cur] == 0)     arr[--dest] = 0;
  dest--;
  }
  }
  };

快乐数 力扣

202. 快乐数

这么说的话，那就只有可能为1或者无限循环(和无限不循环区分)--所以想到环
环的话用快慢双指针去解决
注意:快慢指针的起点都是n   快慢指针一定会在环入口相遇

引申：一定要动手模拟一下示例

代码展示:
class Solution {
public:
int algorithm(int p)
{
int sum = 0;
int q = 0;
while(p>=10)
{
q = p%10;
p/=10;
sum+=q*q;
}
sum+=p*p;
return sum;
}
bool isHappy(int n) {
int slow = n;
int fast = n;
slow = algorithm(n);
fast = algorithm(slow);
while(slow!=fast)
{
slow = algorithm(slow);
fast = algorithm(fast);
fast = algorithm(fast);
}
if(slow == 1)  return true;
else   return false;
}
};

盛最多水的容器 力扣

11. 盛最多水的容器

做法:left放在最左边，right放在最右边

比较完之后，看left和right哪个对应的值小些，就把哪个向另外一边靠近

代码展示:
class Solution {
public:
int maxArea(vector<int>& height) {
  int cur = 0;
  int dest = height.size()-1;
  int max1 = 0;
  while(cur!=dest)
  {
  max1 = max(max1,(dest-cur)*min(height[dest],height[cur])    )     ;
  if(height[cur]<height[dest])    cur++;
  else       dest--;
  }
  return max1;
  }
  };

有效三角形的个数 力扣

611. 有效三角形的个数

相关数学知识: 三角形最小的那两边之和>最大那一边就可以构成三角形了

方法:先给数组排序，然后先固定最大的数，在最大的数的左边用双指针算法去找符合的数;然后再缩小最大的数…

注意:如果nums[left]+nums[right]>nums[c],那right-left就是第二大数下标为rgiht时的总个数，然后right--)

注意区分c和nums[c]!!!

代码展示：
class Solution {
public:
int triangleNumber(vector<int>& nums) {
  sort(nums.begin(),nums.end());
  int c = nums.size()-1;
  int ret = 0;
  while(c>=2)
  {
  int left  = 0;   int right = c-1;
  while(left!=right)
  {
  if((nums[left]+nums[right])>nums[c])//记得加括号
  {
  ret+=right-left;
  right--;
  }
  else    left++;
  }
  c--;
  }
  return ret;
  }
  };

查找总价格为目标值的两个商品 力扣

查找总价格为目标值的两个商品

这个题有单调性，用双指针正好(或者二分算法)–能用双指针肯定优先用双指针

注意:此题没说找不到怎么办，就不用管那种情况，但是!力扣要求所有路径都要有返回值，在最后加个return …就行了，但是要是能转化为vector<int>类型的,比如nullptr就不行

引申:eg: return {1,1};可以被隐式转成vector类型的(函数返回值是vector的情况下)

代码展示:
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
  vector<int>ret;
    int left = 0;
    int right = price.size()-1;
    while(left!=right)
    {
    if(price[left]+price[right]>target)    right--;
    else if(price[left]+price[right]<target)   left++;
    else  {
    ret.push_back(price[left]);
    ret.push_back(price[right]);
    break;
    }
    }
    return ret;
    }
    };

三数之和 力扣

三数之和

这种和怎么样怎么样的一般都排序之后用双指针

这个题跟上面的有效三角形的个数有点像

细节问题:

1.去重

left和right以及固定的那个数都要跳过重复元素(哪个跟哪个比较==才去要注意)–于此同时要避免越界，比如:left一直要<right

补充:当然也可以找出所有结果之后，用unordered_set去重——可是，去面试的时候这两种方法都可能会问到

2.不漏

找到一种结果之后，不能直接break出去，要eg:left++;right--继续寻找

引申:迭代器和下标怎么确立关系:(下标为p)–迭代器连续的那种才行(eg:vector算，list不算)

eg:auto a = ret.begin()+p

  逗号不能用来同时定义两个不同类型的变量

eg:int a = 1,double b = 0;是不行的

引申:题目给的target不要直接拿来运算，不然后续想要原来的就难了
eg:vector>的取名叫vv很好
溢出问题很容易读题时考虑到，后面又忘了--比如应该写long long int 又写成了int

代码展示:
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
  vector<vector<int>> ret;
    sort(nums.begin(),nums.end());
    int i = 0,j = 0;
    for(int k = nums.size()-1;k>=2;k--)
    {
    if(nums[k]<0) break;
    i = 0;j = k-1;
    while(i<j)
    {
    if(nums[i]+nums[j]+nums[k]>0)  j--;
    else if(nums[i]+nums[j]+nums[k]<0)  i++;
    else{
    ret.push_back({nums[i],nums[j],nums[k]});
    i++;j--;
    //去重
    while(nums[i] == nums[i-1]&&i<j)  i++;
    while(nums[j] == nums[j+1]&&i<j)  j--;
    }
    }
    while(nums[k] == nums[k-1]&&k>=2)  k--;
    }
    return ret;
    }
    };