详细介绍:【优选算法】D&C-Mergesort-Harmonies:分治-归并的算法之谐
本篇是优选算法之分治-归并,简单来说就是一个不断分组排序再合并的过程
1.概念解析
什么是分治-归并?
分治归并(基于分治思想的归并排序)是分治算法(Divide and Conquer)在排序问题中的经典应用,核心是通过 “拆分 - 排序 - 合并” 三步,将无序数组转化为有序数组,本质是 “化繁为简、再合简为繁” 的解题思路
2.排序数组
✏️题目描述:

✏️示例:

传送门:排序数组
题解: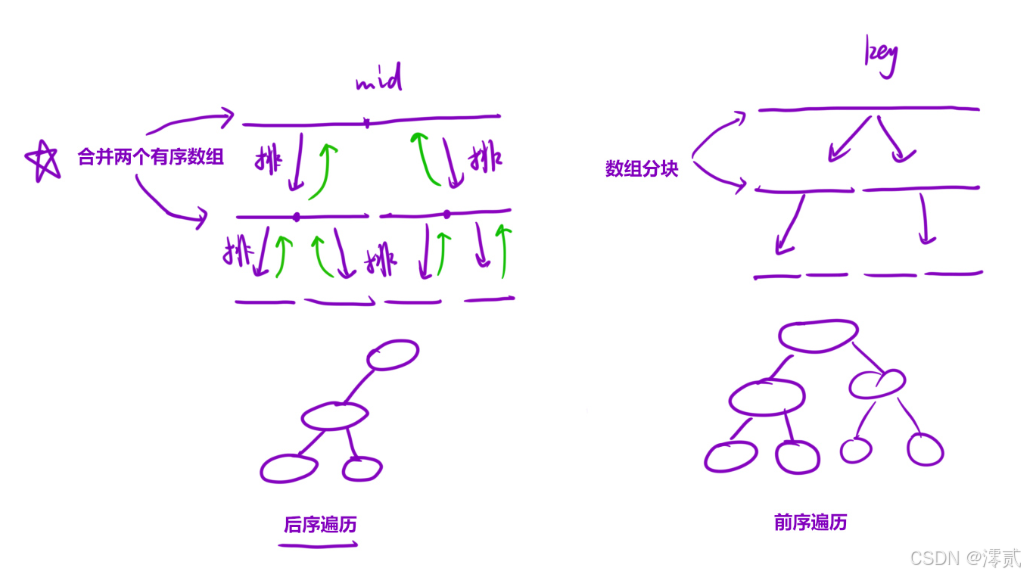
本质上分治归并就是一个后序遍历,而快排就是一个前序遍历,不断向下细分数组,然后从下往上把左右两分支的数组排序并合并,以此向上循环往复
细节问题:
int mid = left + ((right - left) >> 1)相当于int mid = left + ((right - left) / 2),二进制的算法效率更高,且该计算中间值的方法能避免整数溢出最后一步合并数组,
nums[left + j] = tmp[j]而不是nums[j] = tmp[j],是因为left不一定是0,即不一定是对原来的整个数组进行排序,可能只对数组一部分进行排序数组排序并不影响逆序对的计算,因为是左右两部分比较,内部已经在递归过程中计算过了
代码实现:
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
vector<int> tmp;
public:
vector<int> sortArray(vector<int>& nums)
{
tmp.resize(nums.size());
mergeSort(nums, 0, nums.size() - 1);
return nums;
}
void mergeSort(vector<int>& nums, int left, int right)
{
if (left >= right)
{
return;
}
int mid = left + ((right - left) >> 1);
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while (cur1 <= mid && cur2 <= right)
{
tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];
}
while (cur1 <= mid)
{
tmp[i++] = nums[cur1++];
}
while (cur2 <= right)
{
tmp[i++] = nums[cur2++];
}
for (int j = 0; j <= right - left; ++j)
{
nums[left + j] = tmp[j];
}
}
};3.交易逆序对的总数
✏️题目描述:
✏️示例:
传送门:交易逆序对的总数
题解: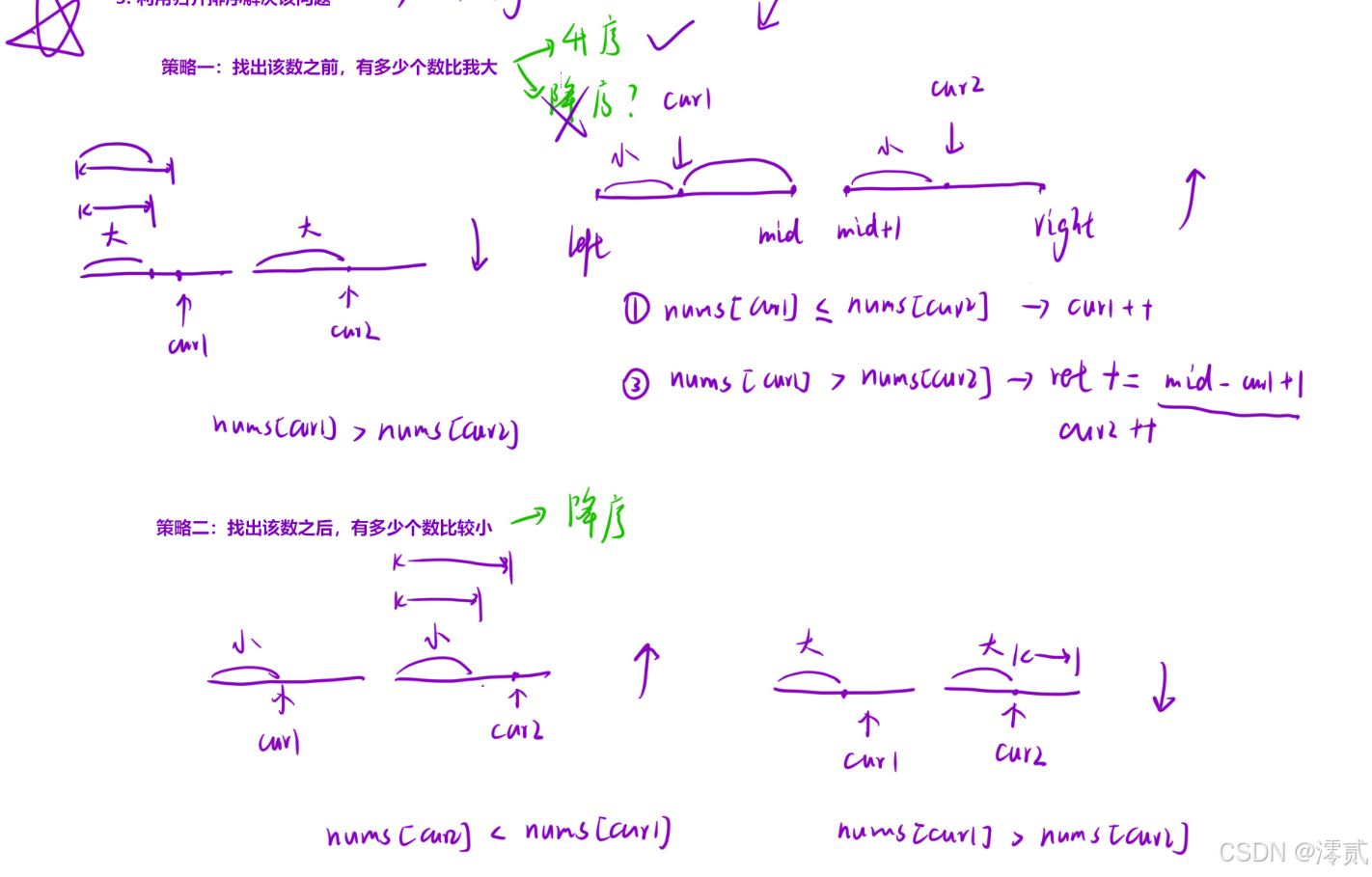
因为归并排序的 “分治 + 有序合并” 特性,完美匹配逆序对统计的核心需求 —— 高效拆分问题、批量计算逆序对,这是暴力枚举做不到的,当 [left,mid] 和 [mid+1,right] 进行互相比较时,如果是升序,获取到 record[cur1] >= record[cur2] 时,由于是有序,所以 cur2 往后都是小于 cur1 对应的数的,所以能直接得到很多对逆序数。用降序也是同理
代码实现:
class Solution
{
vector<int> tmp;
public:
int reversePairs(vector<int>& record)
{
tmp.resize(50010);
return mergeSort(record, 0, record.size() - 1);
}
int mergeSort(vector<int> &record, int left, int right)
{
if(left >= right)
{
return 0;
}
int ret = 0;
int mid = left + ((right - left) >> 1);
ret += mergeSort(record, left, mid);
ret += mergeSort(record, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2 <= right)
{
if(record[cur1] <= record[cur2])
{
tmp[i++] = record[cur1++];
}
else
{
ret += mid - cur1 + 1;
tmp[i++] = record[cur2++];
}
}
while(cur1 <= mid)
{
tmp[i++] = record[cur1++];
}
while(cur2 <= right)
{
tmp[i++] = record[cur2++];
}
for(int j = 0; j < right - left + 1; ++j)
{
record[j + left] = tmp[j];
}
return ret;
}
};4.计算右侧小于当前元素的个数
✏️题目描述:
✏️示例:
传送门:计算右侧小于当前元素的个数
题解: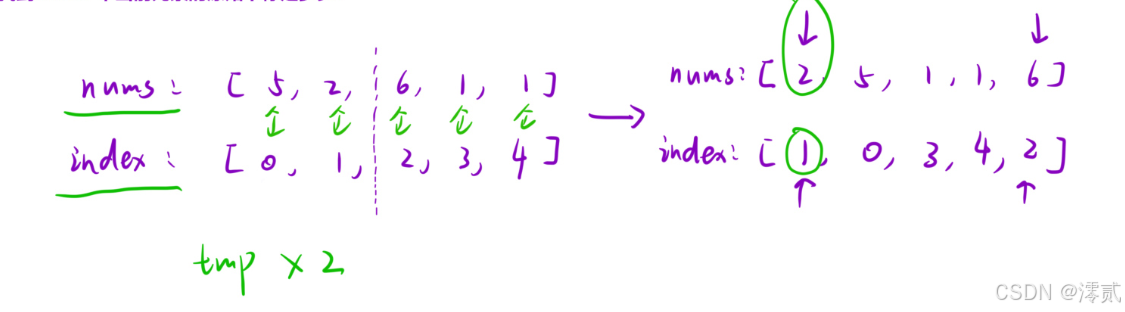
这题和上一题思路基本一致,唯一的难点就是要额外创建一个数组进行值和下表的绑定,因为题目要求的是返回每个 index 对应的值,有人就问了为什么不能用哈希表,可以是可以但是有重复值的话会很麻烦,因此额外创建一个数组进行 index 和值的绑定更方便,index 数组跟着 nums 数组移动就行
代码实现:
class Solution
{
vector<int> ret;
vector<int> index;
int tmpNums[500010];
int tmpindex[500010];
public:
vector<int> countSmaller(vector<int>& nums)
{
int n = nums.size();
ret.resize(n, 0);
index.resize(n);
for(int i = 0; i < n; ++i)
{
index[i] = i;
}
mergeSort(nums, 0, n - 1);
return ret;
}
void mergeSort(vector<int>& nums, int left, int right)
{
if(left >= right)
{
return;
}
int mid = left + ((right - left) >> 1);
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur1] <= nums[cur2])
{
tmpNums[i] = nums[cur2];
tmpindex[i++] = index[cur2++];
}
else
{
ret[index[cur1]] += right - cur2 + 1;
tmpNums[i] = nums[cur1];
tmpindex[i++] = index[cur1++];
}
}
while(cur1 <= mid)
{
tmpNums[i] = nums[cur1];
tmpindex[i++] = index[cur1++];
}
while(cur2 <= right)
{
tmpNums[i] = nums[cur2];
tmpindex[i++] = index[cur2++];
}
for(int j = 0; j < right - left + 1; ++j)
{
nums[j + left] = tmpNums[j];
index[j + left] = tmpindex[j];
}
}
};5.翻转对
✏️题目描述:
✏️示例:
传送门:翻转对
题解: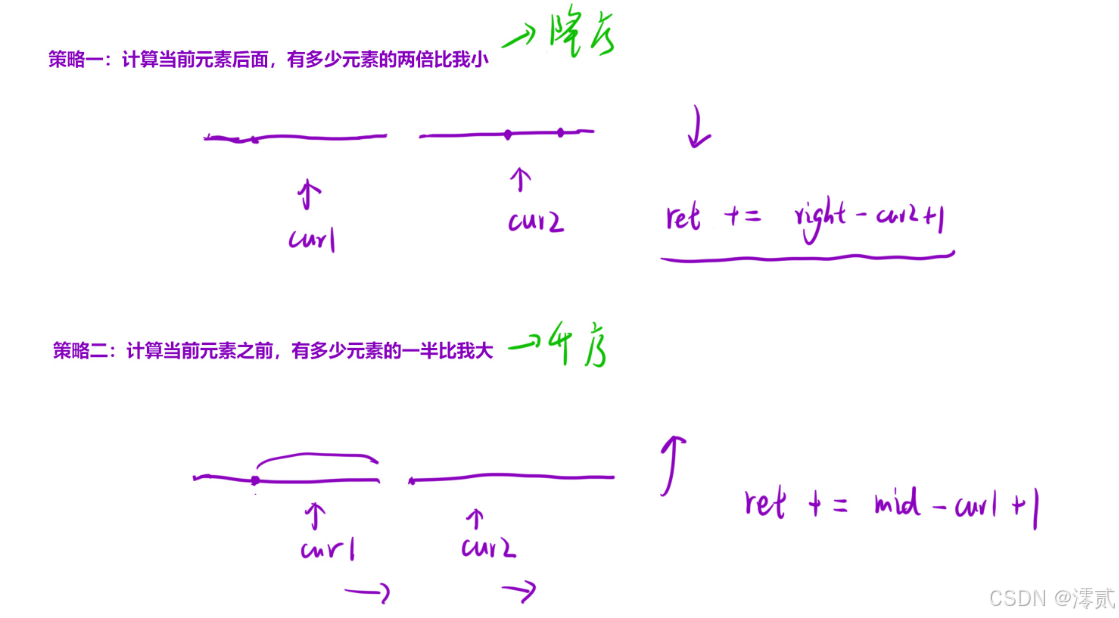
思路还是利用归并解决,但是要提前计算符合题目要求的翻转对,如果在排序过程中进行计算,会漏掉部分翻转对
细节问题:
(long long)nums[cur1] <= 2 * (long long)nums[cur2] 防止溢出
代码实现:
class Solution
{
vector<int> tmp;
int ret = 0;
public:
int reversePairs(vector<int>& nums)
{
tmp.resize(nums.size());
mergeSort(nums, 0, nums.size() - 1);
return ret;
}
void mergeSort(vector<int>& nums, int left, int right)
{
if (left >= right)
{
return;
}
int mid = left + ((right - left) >> 1);
mergeSort(nums, left, mid);zq
mergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while (cur2 <= right)
{
while (cur1 <= mid && (long long)nums[cur1] <= 2 * (long long)nums[cur2])
{
cur1++;
}
if (cur1 > mid)
{
break;
}
ret += mid - cur1 + 1;
cur2++;
}
cur1 = left, cur2 = mid + 1;
while (cur1 <= mid && cur2 <= right)
{
if (nums[cur1] <= nums[cur2])
{
tmp[i++] = nums[cur1++];
}
else
{
tmp[i++] = nums[cur2++];
}
}
while (cur1 <= mid)
{
tmp[i++] = nums[cur1++];
}
while (cur2 <= right)
{
tmp[i++] = nums[cur2++];
}
for (int j = 0; j < right - left + 1; ++j)
{
nums[j + left] = tmp[j];
}
}
};希望读者们多多三连支持
小编会继续更新
你们的鼓励就是我前进的动力!






 浙公网安备 33010602011771号
浙公网安备 33010602011771号