实用指南:链表-双向链表【node3】
双向链表的基本操作
基础结构
每个节点包含三个部分:
- 数据域(Data):存储节点的数据
- 前向指针(Prev):指向前一个节点的引用
- 后向指针(Next):指向后一个节点的引用

// 节点内部类
static class Node {
int data; // 节点存储的数据
Node next; // 指向下一个节点的引用
Node prev; // 指向前一个节点的引用
// 节点构造方法
public Node(int data) {
this.data = data;
this.next = null;
this.prev = null;
}
}
private Node head; // 链表头节点
private Node tail; // 链表尾节点
// 双向链表构造方法
public DoublyLinkedList() {
this.head = null;
this.tail = null;
}单链表VS双链表
单链表
- 每个节点只有一个指向下一个节点的指针
- 只能从头到尾遍历
- 无法直接访问前一个节点
- 内存占用较少
双向链表
- 每个节点有两个指针:一个指向前一个节点,一个指向后一个节点
- 可以从头到尾或从尾到头遍历
- 可以直接访问前一个节点
- 内存占用较多
插入
双向链表的插入操作需要维护前向和后向指针,但可以在任意位置高效地插入新节点。
头部插入
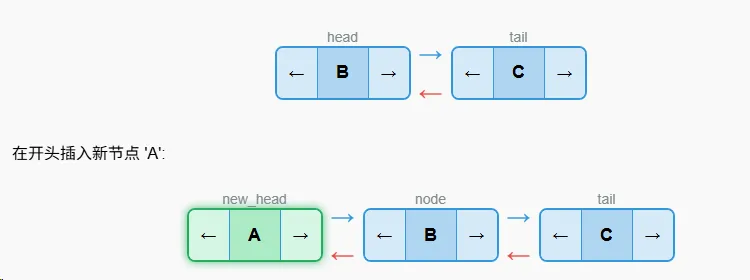
算法步骤:
- 创建新节点
- 将新节点的next指向当前的头节点
- 将当前头节点的prev指向新节点
- 更新头节点为新节点
/**
* 在链表头部插入节点
* @param data 插入的节点数据
*/
public void prepend(int data) {
Node newNode = new Node(data);
// 如果链表为空
if (head == null) {
head = newNode;
tail = newNode;
return;
}
// 将新节点链接到头部
newNode.next = head;
head.prev = newNode;
head = newNode;
}尾部插入
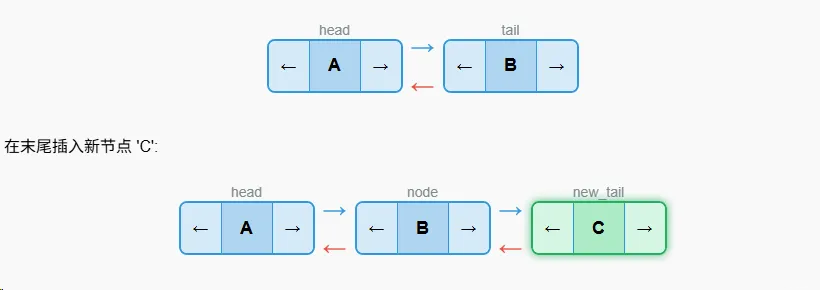
步骤
- 创建新节点
- 将新节点的prev指向当前的尾节点
- 将当前尾节点的next指向新节点
- 更新尾节点为新节点
/**
* 在链表末尾插入节点
* @param data 插入的节点数据
*/
public void append(int data) {
Node newNode = new Node(data);
// 如果链表为空
if (head == null) {
head = newNode;
tail = newNode;
return;
}
// 将新节点链接到尾部
newNode.prev = tail;
tail.next = newNode;
tail = newNode;
}指定位置插入
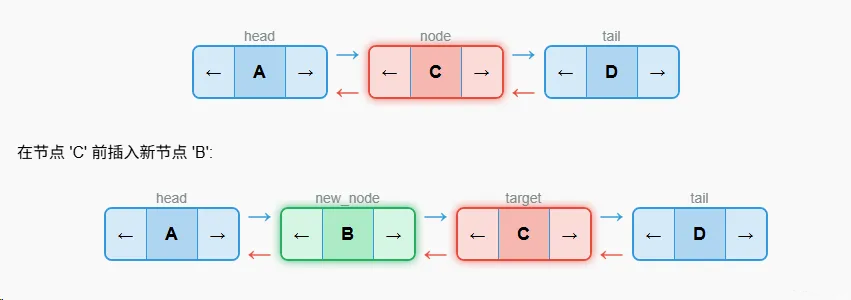
算法**步骤**
- 创建新节点
- 将新节点的next指向目标节点
- 将新节点的prev指向目标节点的prev
- 如果目标节点不是头节点,将目标节点之前的节点的next指向新节点
- 将目标节点的prev指向新节点
- 如果目标节点是头节点,更新头节点为新节点
/**
* 在指定数据的节点前插入新节点
* @param targetData 目标节点的数据
* @param data 新节点的数据
* @return 插入成功返回true,失败返回false
*/
public boolean insertBefore(int targetData, int data) {
// 如果链表为空
if (head == null) {
return false;
}
// 如果目标是头节点
if (head.data == targetData) {
prepend(data);
return true;
}
Node current = head;
// 查找目标节点
while (current != null && current.data != targetData) {
current = current.next;
}
// 如果没有找到目标节点
if (current == null) {
return false;
}
// 创建新节点并插入
Node newNode = new Node(data);
newNode.next = current;
newNode.prev = current.prev;
current.prev.next = newNode;
current.prev = newNode;
return true;
}删除
双向链表的删除操作需要更新节点的前向和后向指针,但相比单链表,它不需要遍历到要删除节点的前一个节点。
删除头节点

算法步骤
- 将头节点更新为当前头节点的next
- 如果新的头节点不为空,将其prev指向NULL
- 如果链表变为空,也更新尾节点为NULL
/**
* 删除头节点
* @return 删除成功返回true,失败返回false
*/
public boolean deleteHead() {
// 如果链表为空
if (head == null) {
return false;
}
// 更新头节点
head = head.next;
// 如果链表不为空,断开新头节点与旧头节点的连接
if (head != null) {
head.prev = null;
}
// 如果链表变为空,同步更新尾节点
else {
tail = null;
}
return true;
}删除尾节点

算法**步骤**
- 将尾节点更新为当前尾节点的prev
- 如果新的尾节点不为空,将其next指向NULL
- 如果链表变为空,也更新头节点为NULL
/**
* 删除尾节点
* @return 删除成功返回true,失败返回false
*/
public boolean deleteTail() {
// 如果链表为空
if (tail == null) {
return false;
}
// 更新尾节点
tail = tail.prev;
// 如果链表不为空,断开新尾节点与旧尾节点的连接
if (tail != null) {
tail.next = null;
}
// 如果链表变为空,同步更新头节点
else {
head = null;
}
return true;
}删除指定节点
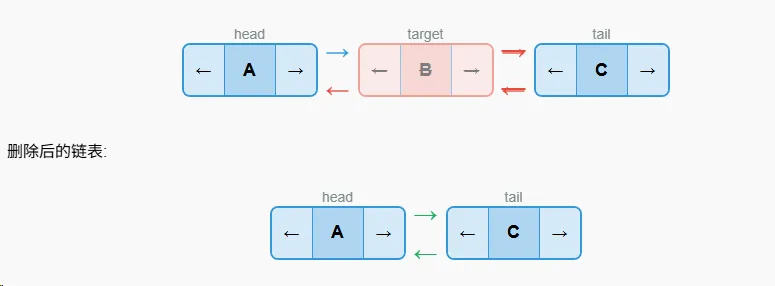
算法**步骤**
- 查找要删除的节点
- 如果节点是头节点,调用delete_head()
- 如果节点是尾节点,调用delete_tail()
- 如果节点是中间节点:
- 将前一个节点的next指向当前节点的next
- 将后一个节点的prev指向当前节点的prev
/**
* 删除指定数据的节点
* @param data 要删除节点的数据
* @return 删除成功返回true,失败返回false
*/
public boolean deleteNode(int data) {
// 如果链表为空
if (head == null) {
return false;
}
// 如果要删除头节点
if (head.data == data) {
return deleteHead();
}
// 如果要删除尾节点
if (tail.data == data) {
return deleteTail();
}
// 查找要删除的节点
Node current = head;
while (current != null && current.data != data) {
current = current.next;
}
// 如果没有找到要删除的节点
if (current == null) {
return false;
}
// 删除中间节点(跳过当前节点)
current.prev.next = current.next;
current.next.prev = current.prev;
return true;
}查找
双向链表可以从头部或尾部开始搜索,这使得查找操作更加灵活
从头部开始查找

/**
* 从头开始搜索指定数据的节点
* @param data 要搜索的数据
* @return 存在返回true,不存在返回false
*/
public boolean search(int data) {
Node current = head;
while (current != null) {
if (current.data == data) {
return true;
}
current = current.next;
}
return false;
}从尾部开始查找

/**
* 从尾开始搜索指定数据的节点
* @param data 要搜索的数据
* @return 存在返回true,不存在返回false
*/
public boolean searchFromTail(int data) {
Node current = tail;
while (current != null) {
if (current.data == data) {
return true;
}
current = current.prev;
}
return false;
}从两端查找
优化查找的策略
对于长链表,我们可以同时从头部和尾部开始查找,这样可以减少查找时间:
- 创建两个指针,一个从头开始,一个从尾开始
- 两个指针同时向中间移动
- 比较两个指针的数据和目标数据
- 当找到目标数据或两个指针相遇或交叉时停止
/**
* 优化搜索(从两端同时向中间搜索)
* @param data 要搜索的数据
* @return 存在返回true,不存在返回false
*/
public boolean optimizedSearch(int data) {
if (head == null) {
return false;
}
Node headPointer = head;
Node tailPointer = tail;
// 两端指针未相遇/未交错时继续搜索
while (headPointer != tailPointer && headPointer.prev != tailPointer) {
// 检查头指针指向的节点
if (headPointer.data == data) {
return true;
}
// 检查尾指针指向的节点
if (tailPointer.data == data) {
return true;
}
// 移动指针
headPointer = headPointer.next;
tailPointer = tailPointer.prev;
// 指针为空则终止(避免异常)
if (headPointer == null || tailPointer == null) {
break;
}
}
// 检查最后一次指针相遇时的节点
if (headPointer != null && headPointer.data == data) {
return true;
}
return false;
}更新
更新操作用于修改链表中特定节点的数据。
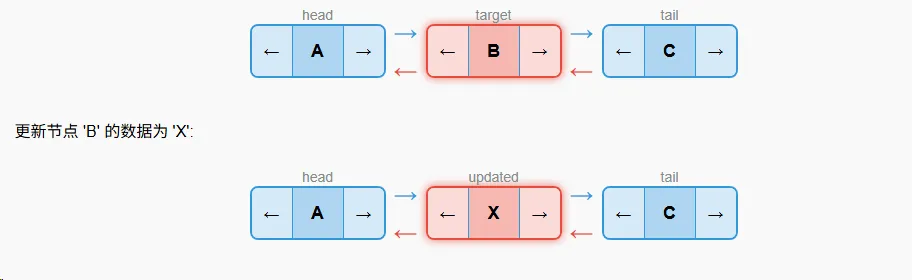
/**
* 更新指定旧数据的节点为新数据
* @param oldData 旧数据
* @param newData 新数据
* @return 更新成功返回true,失败返回false
*/
public boolean updateNode(int oldData, int newData) {
Node current = head;
while (current != null) {
if (current.data == oldData) {
current.data = newData;
return true;
}
current = current.next;
}
// 未找到目标节点
return false;
}遍历
双向链表可以从头到尾或从尾到头进行遍历,这是它相对于单链表的一个优势。
双向链表可以从任意一端开始遍历,这使得某些操作更加高效。例如,如果我们知道要访问的节点更靠近尾部,可以从尾部开始遍历,减少遍历的节点数量。
从头到尾遍历

/**
* 遍历链表(从头到尾)
* @return 存储节点数据的List
*/
public List traverseForward() {
List elements = new ArrayList<>();
Node current = head;
while (current != null) {
elements.add(current.data);
current = current.next;
}
return elements;
} 从尾到头遍历

/**
* 遍历链表(从尾到头)
* @return 存储节点数据的List
*/
public List traverseBackward() {
List elements = new ArrayList<>();
Node current = tail;
while (current != null) {
elements.add(current.data);
current = current.prev;
}
return elements;
} 完整代码
import java.util.ArrayList;
import java.util.List;
/**
* @Author Stringzhua
* @Date 2025/10/23 15:18
* description:
*/
public class DoublyLinkedList {
// 节点内部类
static class Node {
int data; // 节点存储的数据
Node next; // 指向下一个节点的引用
Node prev; // 指向前一个节点的引用
// 节点构造方法
public Node(int data) {
this.data = data;
this.next = null;
this.prev = null;
}
}
private Node head; // 链表头节点
private Node tail; // 链表尾节点
// 双向链表构造方法
public DoublyLinkedList() {
this.head = null;
this.tail = null;
}
/**
* 遍历链表(从头到尾)
* @return 存储节点数据的List
*/
public List traverseForward() {
List elements = new ArrayList<>();
Node current = head;
while (current != null) {
elements.add(current.data);
current = current.next;
}
return elements;
}
/**
* 遍历链表(从尾到头)
* @return 存储节点数据的List
*/
public List traverseBackward() {
List elements = new ArrayList<>();
Node current = tail;
while (current != null) {
elements.add(current.data);
current = current.prev;
}
return elements;
}
/**
* 在链表末尾插入节点
* @param data 插入的节点数据
*/
public void append(int data) {
Node newNode = new Node(data);
// 如果链表为空
if (head == null) {
head = newNode;
tail = newNode;
return;
}
// 将新节点链接到尾部
newNode.prev = tail;
tail.next = newNode;
tail = newNode;
}
/**
* 在链表头部插入节点
* @param data 插入的节点数据
*/
public void prepend(int data) {
Node newNode = new Node(data);
// 如果链表为空
if (head == null) {
head = newNode;
tail = newNode;
return;
}
// 将新节点链接到头部
newNode.next = head;
head.prev = newNode;
head = newNode;
}
/**
* 在指定数据的节点前插入新节点
* @param targetData 目标节点的数据
* @param data 新节点的数据
* @return 插入成功返回true,失败返回false
*/
public boolean insertBefore(int targetData, int data) {
// 如果链表为空
if (head == null) {
return false;
}
// 如果目标是头节点
if (head.data == targetData) {
prepend(data);
return true;
}
Node current = head;
// 查找目标节点
while (current != null && current.data != targetData) {
current = current.next;
}
// 如果没有找到目标节点
if (current == null) {
return false;
}
// 创建新节点并插入
Node newNode = new Node(data);
newNode.next = current;
newNode.prev = current.prev;
current.prev.next = newNode;
current.prev = newNode;
return true;
}
/**
* 删除头节点
* @return 删除成功返回true,失败返回false
*/
public boolean deleteHead() {
// 如果链表为空
if (head == null) {
return false;
}
// 更新头节点
head = head.next;
// 如果链表不为空,断开新头节点与旧头节点的连接
if (head != null) {
head.prev = null;
}
// 如果链表变为空,同步更新尾节点
else {
tail = null;
}
return true;
}
/**
* 删除尾节点
* @return 删除成功返回true,失败返回false
*/
public boolean deleteTail() {
// 如果链表为空
if (tail == null) {
return false;
}
// 更新尾节点
tail = tail.prev;
// 如果链表不为空,断开新尾节点与旧尾节点的连接
if (tail != null) {
tail.next = null;
}
// 如果链表变为空,同步更新头节点
else {
head = null;
}
return true;
}
/**
* 删除指定数据的节点
* @param data 要删除节点的数据
* @return 删除成功返回true,失败返回false
*/
public boolean deleteNode(int data) {
// 如果链表为空
if (head == null) {
return false;
}
// 如果要删除头节点
if (head.data == data) {
return deleteHead();
}
// 如果要删除尾节点
if (tail.data == data) {
return deleteTail();
}
// 查找要删除的节点
Node current = head;
while (current != null && current.data != data) {
current = current.next;
}
// 如果没有找到要删除的节点
if (current == null) {
return false;
}
// 删除中间节点(跳过当前节点)
current.prev.next = current.next;
current.next.prev = current.prev;
return true;
}
/**
* 从头开始搜索指定数据的节点
* @param data 要搜索的数据
* @return 存在返回true,不存在返回false
*/
public boolean search(int data) {
Node current = head;
while (current != null) {
if (current.data == data) {
return true;
}
current = current.next;
}
return false;
}
/**
* 从尾开始搜索指定数据的节点
* @param data 要搜索的数据
* @return 存在返回true,不存在返回false
*/
public boolean searchFromTail(int data) {
Node current = tail;
while (current != null) {
if (current.data == data) {
return true;
}
current = current.prev;
}
return false;
}
/**
* 优化搜索(从两端同时向中间搜索)
* @param data 要搜索的数据
* @return 存在返回true,不存在返回false
*/
public boolean optimizedSearch(int data) {
if (head == null) {
return false;
}
Node headPointer = head;
Node tailPointer = tail;
// 两端指针未相遇/未交错时继续搜索
while (headPointer != tailPointer && headPointer.prev != tailPointer) {
// 检查头指针指向的节点
if (headPointer.data == data) {
return true;
}
// 检查尾指针指向的节点
if (tailPointer.data == data) {
return true;
}
// 移动指针
headPointer = headPointer.next;
tailPointer = tailPointer.prev;
// 指针为空则终止(避免异常)
if (headPointer == null || tailPointer == null) {
break;
}
}
// 检查最后一次指针相遇时的节点
if (headPointer != null && headPointer.data == data) {
return true;
}
return false;
}
/**
* 更新指定旧数据的节点为新数据
* @param oldData 旧数据
* @param newData 新数据
* @return 更新成功返回true,失败返回false
*/
public boolean updateNode(int oldData, int newData) {
Node current = head;
while (current != null) {
if (current.data == oldData) {
current.data = newData;
return true;
}
current = current.next;
}
// 未找到目标节点
return false;
}
/**
* 打印链表(格式:data <-> data <-> ...)
*/
public void printList() {
List elements = new ArrayList<>();
Node current = head;
while (current != null) {
elements.add(String.valueOf(current.data));
current = current.next;
}
System.out.println(String.join(" <-> ", elements));
}
public static void main(String[] args) {
// 1. 创建双向链表实例
DoublyLinkedList dll = new DoublyLinkedList();
// 2. 向链表末尾插入元素
dll.append(10);
dll.append(20);
dll.append(30);
System.out.println("插入末尾后:");
dll.printList(); // 输出: 10 <-> 20 <-> 30
// 3. 向链表头部插入元素
dll.prepend(5);
System.out.println("插入头部后:");
dll.printList(); // 输出: 5 <-> 10 <-> 20 <-> 30
// 4. 在指定节点前插入元素
dll.insertBefore(20, 15);
System.out.println("在20前插入15后:");
dll.printList(); // 输出: 5 <-> 10 <-> 15 <-> 20 <-> 30
// 5. 删除头节点
dll.deleteHead();
System.out.println("删除头节点后:");
dll.printList(); // 输出: 10 <-> 15 <-> 20 <-> 30
// 6. 删除尾节点
dll.deleteTail();
System.out.println("删除尾节点后:");
dll.printList(); // 输出: 10 <-> 15 <-> 20
// 7. 删除中间节点
dll.deleteNode(15);
System.out.println("删除15后:");
dll.printList(); // 输出: 10 <-> 20
// 8. 更新节点数据
dll.updateNode(20, 25);
System.out.println("更新20为25后:");
dll.printList(); // 输出: 10 <-> 25
// 9. 搜索元素(从头开始)
System.out.println("搜索10是否存在: " + dll.search(10)); // 输出: true
System.out.println("搜索25是否存在: " + dll.search(25)); // 输出: true
System.out.println("搜索15是否存在: " + dll.search(15)); // 输出: false
// 10. 从尾部开始搜索
System.out.println("从尾部搜索25是否存在: " + dll.searchFromTail(25)); // 输出: true
// 11. 优化搜索(双向同时搜索)
System.out.println("优化搜索10是否存在: " + dll.optimizedSearch(10)); // 输出: true
System.out.println("优化搜索30是否存在: " + dll.optimizedSearch(30)); // 输出: false
// 12. 反向遍历链表
System.out.println("反向遍历链表: " + dll.traverseBackward()); // 输出: [25, 10]
// 13. 测试插入到不存在的节点前
boolean success = dll.insertBefore(99, 100);
System.out.println("尝试插入到不存在的节点99前: " + (success ? "成功" : "失败")); // 输出: 失败
}
} 时间空间复杂度分析
操作
- 访问元素
- 头部/尾部插入
- 中间插入(已知位置)
- 中间插入(未知位置)
- 头部/尾部删除
- 中间删除(已知位置)
- 中间删除(未知位置)
- 查找元素
时间复杂度
- O(n)
- O(1)
- O(1)
- O(n)
- O(1)
- O(1)
- O(n)
- O(n)
说明
- 必须从头或尾遍历
- 直接操作头尾指针
- 只需更新前后指针
- 需要先查找位置
- 直接操作头尾指针
- 只需更新前后指针
- 需要先查找位置
- 最坏情况需要遍历整个链表
双向链表的空间复杂度为O(n),其中n是链表中的节点数。相比于单链表,双向链表每个节点需要额外的空间来存储prev指针,这使得双向链表的空间效率略低于单链表。
双向链表的主要优势在于:
- 可以从两个方向遍历
- 删除和插入操作更加高效(不需要找前驱节点)
- 可以直接访问前一个节点
双向链表的主要劣势在于:
- 每个节点需要额外的空间存储prev指针
- 实现和维护相对复杂





 浙公网安备 33010602011771号
浙公网安备 33010602011771号