穷举 vs 暴搜 vs 深搜 vs 回溯 vs 剪枝 - 详解
穷举 vs 暴搜 vs 深搜 vs 回溯 vs 剪枝
什么是回溯算法
回溯算法是一种经典的递归算法,通常用于解决组合问题、排列问题和搜索问题等。
回溯算法的基本思想:从一个初始状态开始,按照一定的规则向前搜索,当搜索到某个状态无法前进时,回退到前一个状态,再按照其他的规则搜索。回溯算法在搜索过程中维护一个状态树,通过遍历状态树来实现对所有可能解的搜索。
回溯算法的核心思想:“试错”,即在搜索过程中不断地做出选择,如果选择正确,则继续向前搜索;否则,回退到上一个状态,重新做出选择。回溯算法通常用于解决具有多个解,且每个解都需要搜索才能找到的问题。
回溯算法的模板
void backtrack(vector& path, vector& choice, ...) {
// 满足结束条件
if (/* 满足结束条件 */) {
// 将路径添加到结果集中
res.push_back(path);
return;
}
// 遍历所有选择
for (int i = 0; i < choices.size(); i++) {
// 做出选择
path.push_back(choices[i]);
// 做出当前选择后继续搜索
backtrack(path, choices);
// 撤销选择
path.pop_back();
}
} 其中,path 表示当前已经做出的选择,choices 表示当前可以做的选择。在回溯算法中,我们需要做出选择,然后递归地调用回溯函数。如果满足结束条件,则将当前路径添加到结果集中;否则,我们需要撤销选择,回到上一个状态,然后继续搜索其他的选择。
回溯算法的时间复杂度通常较高,因为它需要遍历所有可能的解。但是,回溯算法的空间复杂度较低,因为它只需要维护一个状态树。在实际应用中,回溯算法通常需要通过剪枝等方法进行优化,以减少搜索的次数,从而提高算法的效率。
回溯算法的应用
组合问题
组合问题是指从给定的一组数(不重复)中选取出所有可能的 k 个数的组合。例如,给定数集 [1,2,3],要求选取 k=2 个数的所有组合。
结果为:
[1,2]
[1,3]
[2,3]排列问题
排列问题是指从给定的一组数(不重复)中选取出所有可能的 k 个数的排列。例如,给定数集 [1,2,3],要求选取 k=2 个数的所有排列。
结果为:
[1,2]
[2,1]
[1,3]
[3,1]
[2,3]
[3,2]子集问题
子集问题是指从给定的一组数中选取出所有可能的子集,其中每个子集中的元素可以按照任意顺序排列。例如,给定数集 [1,2,3],要求选取所有可能的子集。
结果为:
[]
[1]
[2]
[3]
[1,2]
[1,3]
[2,3]
[1,2,3]总结
回溯算法是一种非常重要的算法,可以解决许多组合问题、排列问题和搜索问题等。回溯算法的核心思想是搜索状态树,通过遍历状态树来实现对所有可能解的搜索。回溯算法的模板非常简单,但是实现起来需要注意一些细节,比如如何做出选择、如何撤销选择等。
其他的我们之前练习的习题应该都是能很好的理解!,但是我想说的是,记模板是没有用的,我们记忆的是模板解题的思想,最终我们要解答这些类型的题目,都是要我们画好决策树的!
题目练习
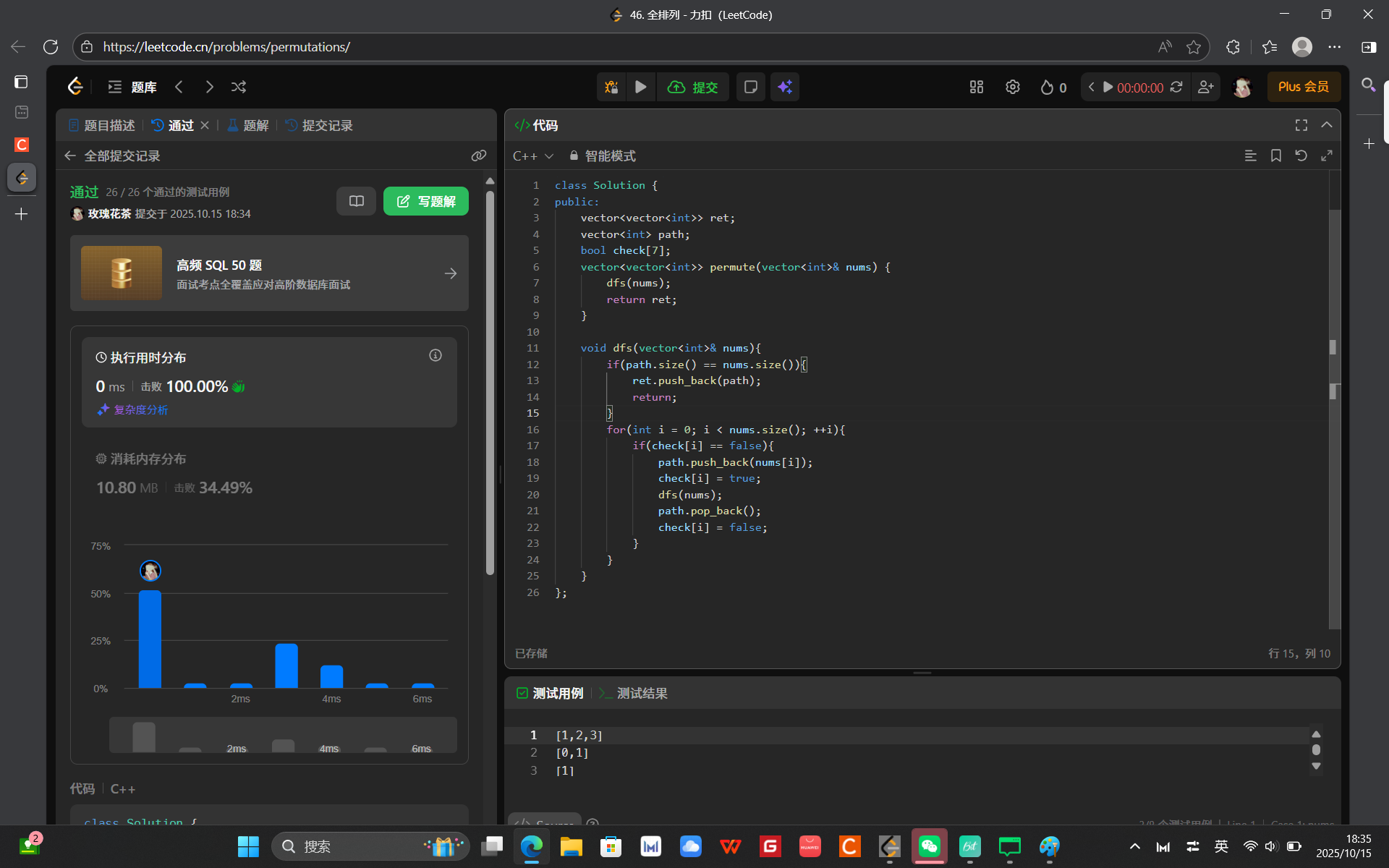
46. 全排列 - 力扣(LeetCode)
解法:
算法思路:
这是典型的回溯题目,需要在每一个位置上考虑所有可能情况且不能重复。通过深度优先搜索的方式,不断枚举每个数在当前位置的可能性,并回溯到上一个状态,直到枚举完所有可能性,得到正确结果。
每个数能否放入当前位置,只需判断该数之前是否出现。具体可通过递归函数 backtrack 和标记数组 visited 实现全排列。
递归函数设计:
void backtrack(vector>& res, vector& nums,
vector& visited, vector& ans, int step, int len) 参数:step(当前需要填入的位置),len(数组长度);
返回值:无;
函数作用:查找所有合理的排列并存储在答案列表中。
递归流程:
定义二维数组 res 存放所有可能排列,一维数组 ans 存放每个状态的排列,一维数组 visited 标记元素,从第一个位置开始递归;
每个递归状态维护步数 step,表示当前已处理数字个数;
递归结束条件:当 step 等于 nums 数组长度时,说明所有数字处理完毕,将当前数组存入结果;
每个递归状态枚举所有下标 i,若下标未被标记,使用 nums 数组中当前下标的元素:
a. 将
visited[i]标记为1;b.
ans数组中第step个元素被nums[i]覆盖;c. 对第
step + 1个位置进行递归;d. 将
visited[i]重新赋值为0,表示回溯;
最后返回 res。
特别地,可不使用标记数组,直接遍历 step 之后的未被使用元素,将其与需要递归的位置交换即可。

class Solution {
public:
vector> ret;
vector path;
bool check[7];
vector> permute(vector& nums) {
dfs(nums);
return ret;
}
void dfs(vector& nums){
if(path.size() == nums.size()){
ret.push_back(path);
return;
}
for(int i = 0; i < nums.size(); ++i){
if(check[i] == false){
path.push_back(nums[i]);
check[i] = true;
dfs(nums);
path.pop_back();
check[i] = false;
}
}
}
}; 
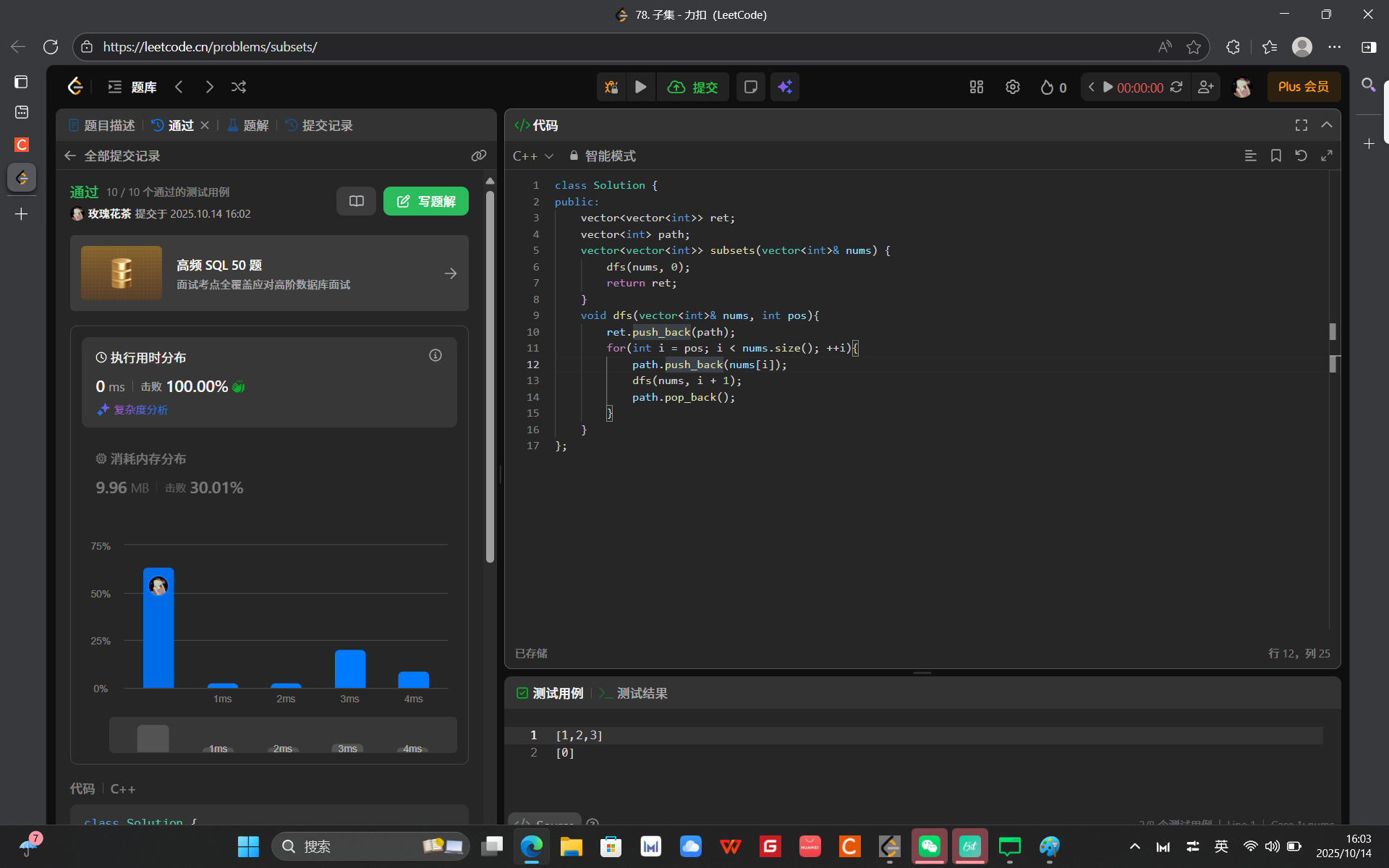
78. 子集 - 力扣(LeetCode)
解法:
算法思路:
为了获得 nums 数组的所有子集,需要对数组中的每个元素进行选择或不选择的操作,nums 数组一定存在 个子集。对于查找子集,可定义一个数组记录当前状态,并对其进行递归。
每个元素有两种选择:1. 不进行任何操作;2. 将其添加至当前状态的集合。在递归时需保证递归结束时当前状态与递归操作前的状态不变,当选择进行步骤 2 递归时,当前状态会变化,因此需在递归结束时撤回添加操作,即进行回溯。
递归函数设计:
void dfs(vector>& res, vector& ans,
vector& nums, int step) 参数:
step(当前需要处理的元素下标);返回值:无;
函数作用:查找集合的所有子集并存储在答案列表中。
递归流程:
递归结束条件:如果当前需要处理的元素下标越界,则记录当前状态并直接返回;
在递归过程中,对于每个元素,有两种选择:
- 不选择当前元素,直接递归到下一个元素;
- 选择当前元素,将其添加到数组末尾后递归到下一个元素,然后在递归结束时撤回添加操作;
所有符合条件的状态都被记录下来,返回即可。
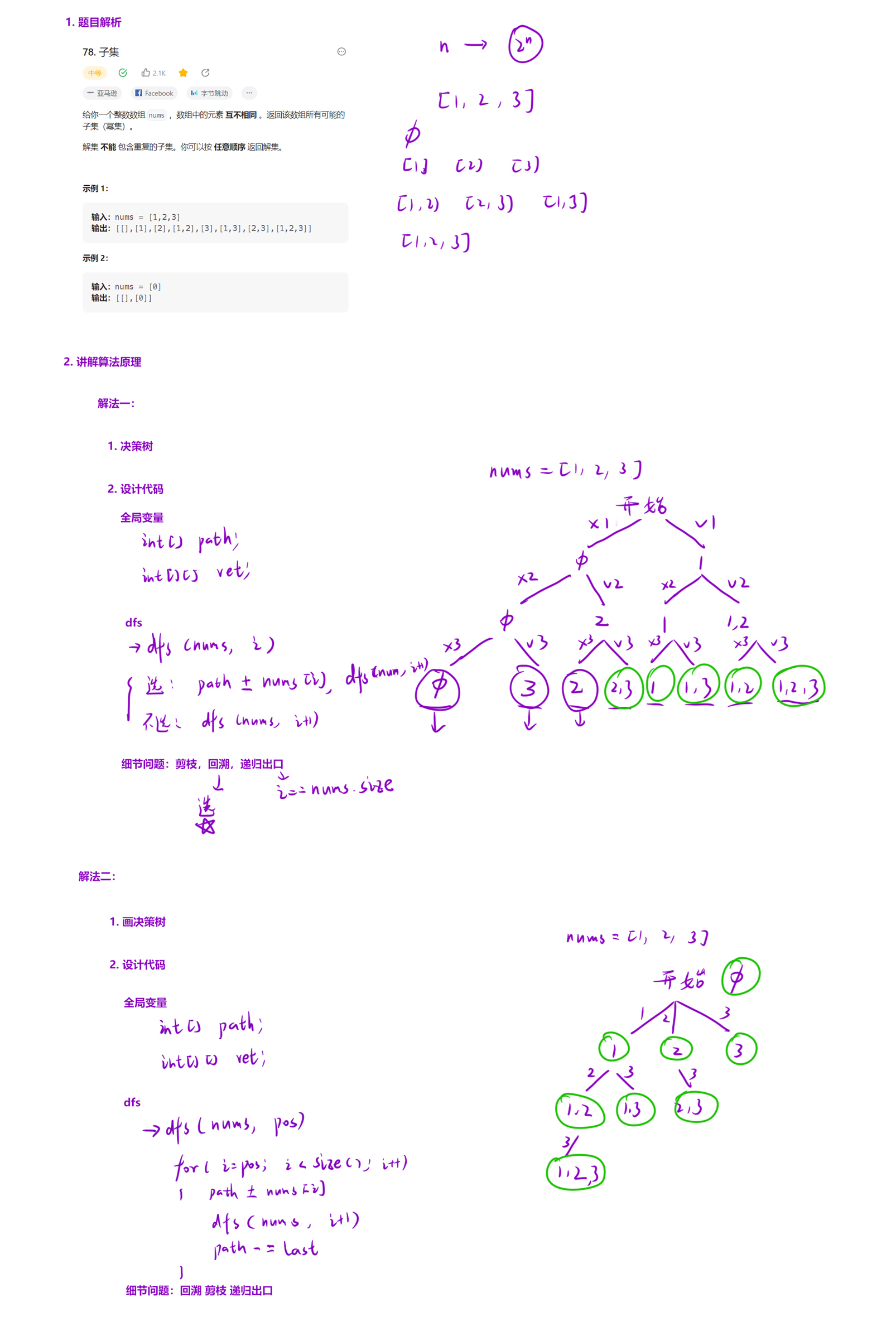
解法一:
class Solution {
public:
vector> ret;
vector path;
vector> subsets(vector& nums) {
dfs(nums, 0);
return ret;
}
void dfs(vector& nums, int pos){
if(pos == nums.size()){
ret.push_back(path);
return;
}
// 选
path.push_back(nums[pos]);
dfs(nums, pos + 1);
path.pop_back();
// 不选
dfs(nums, pos + 1);
}
}; 解法二:
class Solution {
public:
vector> ret;
vector path;
vector> subsets(vector& nums) {
dfs(nums, 0);
return ret;
}
void dfs(vector& nums, int pos){
ret.push_back(path);
for(int i = pos; i < nums.size(); ++i){
path.push_back(nums[i]);
dfs(nums, i + 1);
path.pop_back();
}
}
}; 
综合练习
1863. 找出所有子集的异或总和再求和 - 力扣(LeetCode)
解法(递归):
算法思路:
所有子集可解释为每个元素选择在或不在一个集合中(因此,子集有 \(2^n\) 个)。本题需求出所有子集,将它们的异或和相加。因异或操作满足交换律,所以可定义一个变量,直接记录当前状态的异或和。使用递归保存当前集合的状态(异或和),选择将当前元素添加至当前状态与否,并依次递归数组中下一个元素。当递归到空元素时,表示所有元素都被考虑到,记录当前状态(将当前状态的异或和添加至答案中)。
递归函数设计:
void dfs(int val, int idx, vector<int>& nums)
参数:
val(当前状态的异或和),idx(当前需要处理的元素下标,处理过程:选择将其添加至当前状态或不进行操作);返回值:无;
函数作用:选择对元素进行添加与否处理。
递归流程:
递归结束条件:当前下标与数组长度相等,即已经越界,表示已经考虑到所有元素;
- 将当前异或和添加至答案中,并返回;
考虑将当前元素添加至当前状态,当前状态更新为与当前元素值的异或和,然后递归下一个元素;
考虑不选择当前元素,当前状态不变,直接递归下一个元素;

class Solution {
public:
int sum, path;
int subsetXORSum(vector& nums) {
dfs(nums, 0);
return sum;
}
void dfs(vector& nums, int pos){
sum += path;
for(int i = pos; i < nums.size(); ++i){
path ^= nums[i];
dfs(nums, i + 1);
path ^= nums[i];
}
}
}; 
47. 全排列 II - 力扣(LeetCode)
解法:
算法思路:
因题目不要求返回排列顺序,可先对初始状态排序,把相同元素放在相邻位置,方便后续操作。由于重复元素存在,全排列时可能出现重复排列。为避免这种情况,需对相同元素定义规则:相同元素按排序后的下标顺序出现在排列中,若元素 s 出现 x 次,排序后第 2 个 s 必在第 1 个 s 后,第 3 个 s 必在第 2 个 s 后,以此类推;若当前元素的前一个相同元素未出现在当前状态数组,当前元素也不能直接放入,保证相同元素排列顺序与排序后一致。通过深度优先搜索,枚举每个数在当前位置的可能性,递归结束时回溯到上一状态,直到枚举完所有可能性。
递归函数设计:
void backtrack(vector<int>& nums, int idx)
参数:
idx(当前需要填入的位置);返回值:无;
函数作用:查找所有合理的排列并存储在答案列表中。
递归流程:
定义二维数组
ans存放所有可能排列,一维数组perm存放每个状态的排列,一维数组visited标记元素,从第一个位置开始递归;每个递归状态维护步数
idx,表示当前已处理数字个数;递归结束条件:当
idx等于nums数组长度时,说明所有数字处理完毕,将当前数组存入结果;每个递归状态枚举所有下标
i,若下标未被标记,且在它之前的相同元素被标记过,则使用nums数组中当前下标的元素:a. 将
visited[i]标记为1;b. 将
nums[i]添加至perm数组末尾;c. 对第
idx + 1个位置进行递归;d. 将
visited[i]重新赋值为0,并删除perm末尾元素表示回溯;
最后返回
ans。
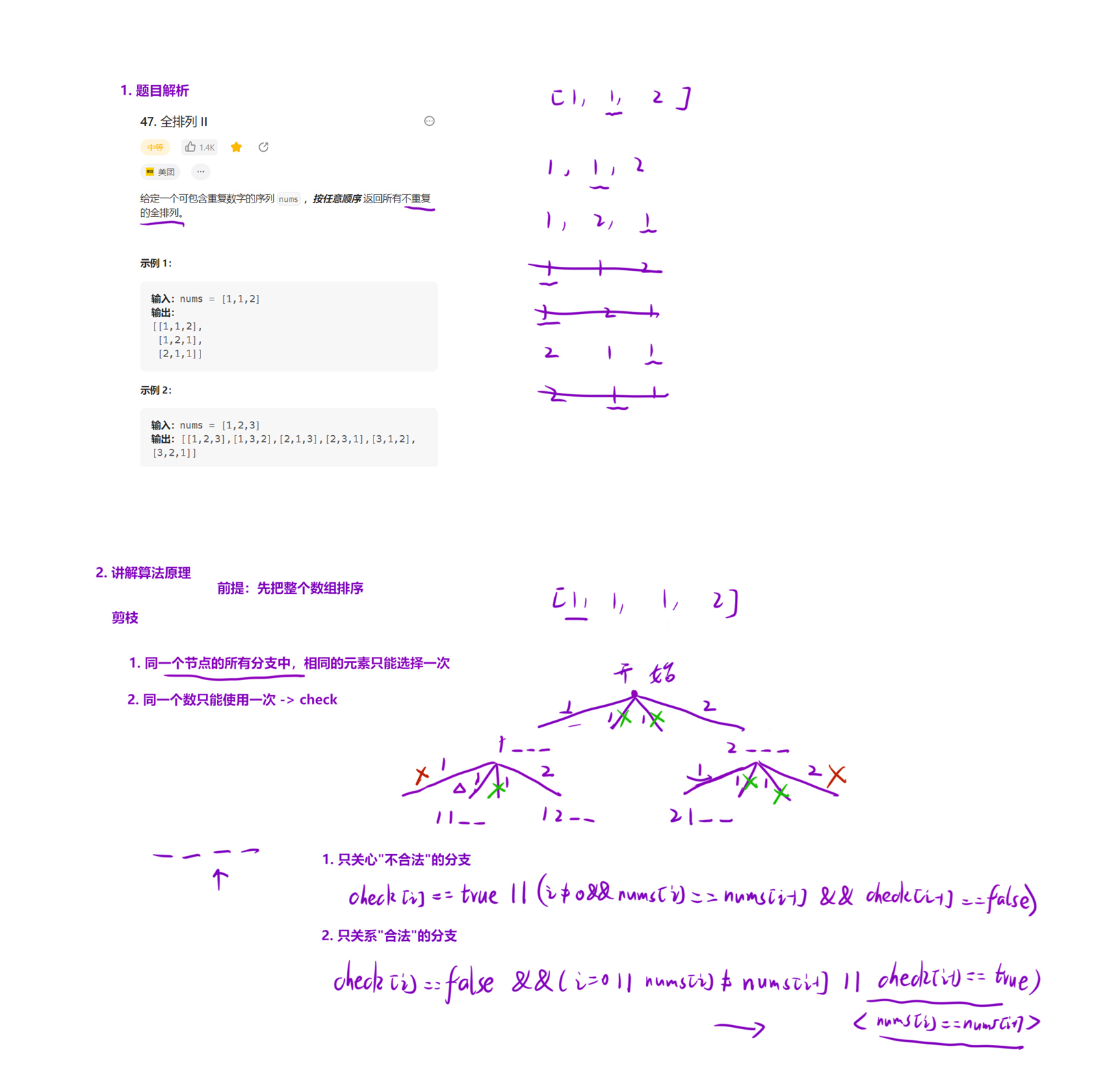
class Solution {
public:
vector> ret;
vector path;
bool check[9];
vector> permuteUnique(vector& nums) {
sort(nums.begin(), nums.end());
dfs(nums, 0);
return ret;
}
void dfs(vector& nums, int pos){
if(pos == nums.size()){
ret.push_back(path);
return;
}
for(int i = 0; i < nums.size(); ++i){
if(check[i] || (i && nums[i] == nums[i - 1] && !check[i - 1])) continue;
path.push_back(nums[i]);
check[i] = true;
dfs(nums, pos + 1);
path.pop_back();
check[i] = false;
}
}
}; 
17. 电话号码的字母组合 - 力扣(LeetCode)
解法:
算法思路:
每个位置可选择的字符与其他位置不冲突,无需标记已出现字符,只需将每个数字对应的字符依次填入字符串进行递归,回溯时撤销填入操作。递归前需定义字典 phoneMap,记录 2 - 9 各自对应的字符。
递归函数设计:
void backtrack(unordered_map<char, string>& phoneMap, string& digits, int index)
参数:
index(已经处理的元素个数),ans(字符串当前状态),res(所有成立的字符串);返回值:无;
函数作用:查找所有合理的字母组合并存储在答案列表中。
递归函数流程:
递归结束条件:当
index等于digits的长度时,将ans加入到res中并返回;取出当前处理的数字
digit,根据phoneMap取出对应的字母列表letters;遍历字母列表
letters,将当前字母加入到组合字符串ans的末尾,然后递归处理下一个数字(传入index + 1,表示处理下一个数字);递归处理结束后,将加入的字母从
ans的末尾删除,表示回溯;最终返回
res即可。

class Solution {
public:
vector ret;
string path;
string hash[10] = { "","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz" };
vector letterCombinations(string digits) {
if(digits == "") return ret;
dfs(digits, 0);
return ret;
}
void dfs(string& digits, int pos) {
if(pos == digits.size()) {
ret.push_back(path);
return;
}
for(auto ch : hash[digits[pos] - '0']) {
path.push_back(ch);
dfs(digits, pos + 1);
path.pop_back();
}
}
}; 
后面还有十几道综合练习!等后续~~~





 浙公网安备 33010602011771号
浙公网安备 33010602011771号