700.二叉搜索树中的搜索（二叉树算法） - 实践

700.二叉搜索树中的搜索

力扣题目地址

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

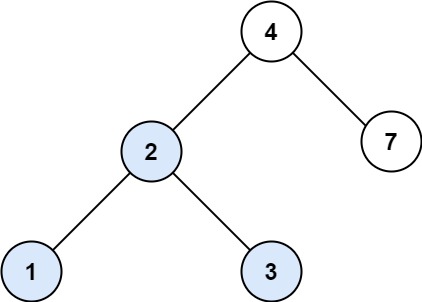
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

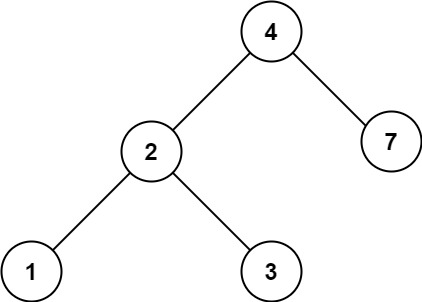
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 树中节点数在 [1, 5000] 范围内
• 1 <= Node.val <= 107
• root 是二叉搜索树
• 1 <= val <= 107

算法公开课

《代码随想录》算法视频公开课 (opens new window)：不愧是搜索树，这次搜索有方向了！| LeetCode：700.二叉搜索树中的搜索 (opens new window)，相信结合视频在看本篇题解，更有助于大家对本题的理解。

#思路

之前我们讲的都是普通二叉树，那么接下来看看二叉搜索树。

在关于二叉树，你该了解这些！ (opens new window)中，我们已经讲过了二叉搜索树。

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

本题，其实就是在二叉搜索树中搜索一个节点。那么我们来看看应该如何遍历。

#递归法

1. 确定递归函数的参数和返回值

递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。

代码如下：

TreeNode* searchBST(TreeNode* root, int val)

1. 确定终止条件

如果root为空，或者找到这个数值了，就返回root节点。

if (root == NULL || root->val == val) return root;

1. 确定单层递归的逻辑

看看二叉搜索树的单层递归逻辑有何不同。

因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。

如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。

代码如下：

TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;

很多录友写递归函数的时候 习惯直接写 searchBST(root->left, val)，却忘了 递归函数还有返回值。!!!我就是错在这一步！

递归函数的返回值是什么? 是 左子树如果搜索到了val，要将该节点返回。 如果不用一个变量将其接住，那么返回值不就没了。

所以要 result = searchBST(root->left, val)。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;       // 节点存储的值
 *     TreeNode left; // 指向左子节点的引用
 *     TreeNode right;// 指向右子节点的引用
 *     TreeNode() {}  // 默认构造函数
 *     TreeNode(int val) { this.val = val; }                // 构造函数：仅值
 *     TreeNode(int val, TreeNode left, TreeNode right) {   // 构造函数：值+左右子树
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /**
     * 在二叉搜索树（BST）中查找值为 val 的节点（LeetCode 第700题：Search in a Binary Search Tree）
     *
     * 使用递归方式实现深度优先搜索（DFS），利用 BST 的性质（左 < 根 < 右）
     * 来决定搜索方向，避免无效分支。
     *
     * @param root BST 的根节点
     * @param val  要查找的目标值
     * @return 如果存在值为 val 的节点，则返回该节点；否则返回 null
     */
    public TreeNode searchBST(TreeNode root, int val) {
        // 调用递归辅助方法进行实际查找
        return searchBST1(root, val);
    }
    /**
     * 递归辅助方法：在以 root 为根的子树中查找值为 val 的节点
     *
     * @param root 当前递归到的节点
     * @param val  目标值
     * @return 找到则返回目标节点，否则返回 null
     */
    public TreeNode searchBST1(TreeNode root, int val) {
        // 基础情况1：当前节点为空（到达叶子的子节点），说明未找到目标值
        if (root == null) return null;
        // 基础情况2：当前节点的值等于目标值，找到目标，直接返回该节点
        if (root.val == val) return root;
        // 定义结果变量，用于接收递归调用的返回值
        TreeNode res = null;
        // 情况1：当前节点值大于目标值 → 目标应在左子树中
        if (root.val > val && root.left != null) {
            // 递归搜索左子树，并将结果赋值给 res
            res = searchBST1(root.left, val);
        }
        // 情况2：当前节点值小于目标值 → 目标应在右子树中
        // 注意：这里使用的是独立的 if，不是 else if
        if (root.val < val && root.right != null) {
            // 递归搜索右子树，并将结果赋值给 res（会覆盖前面的 res）
            res = searchBST1(root.right, val);
        }
        // 返回查找结果
        // 如果两个 if 都没执行，res 保持为 null
        // 如果某个分支找到了，res 就是目标节点
        return res;
    }
}

迭代法

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。

对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。

而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。

例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。

中间节点如果大于3就向左走，如果小于3就向右走，如图：

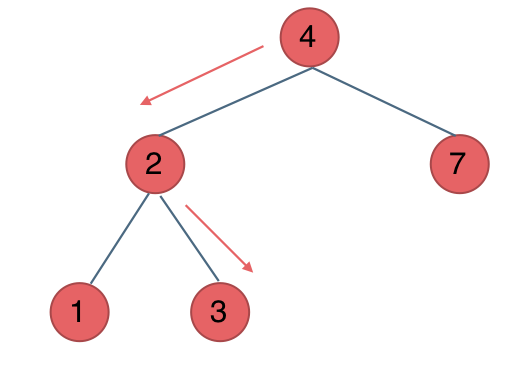
所以迭代法代码如下：

class Solution {
    // 迭代，利用二叉搜索树特点，优化，可以不需要栈
    public TreeNode searchBST(TreeNode root, int val) {
        while (root != null)
            if (val < root.val) root = root.left;
            else if (val > root.val) root = root.right;
            else return root;
        return null;
    }
}

下面这个是我自己想的（使用了空间咯咯哒）：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;       // 节点存储的值
 *     TreeNode left; // 指向左子节点的引用
 *     TreeNode right;// 指向右子节点的引用
 *     TreeNode() {}  // 默认构造函数
 *     TreeNode(int val) { this.val = val; }                // 构造函数：仅值
 *     TreeNode(int val, TreeNode left, TreeNode right) {   // 构造函数：值+左右子树
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /**
     * 在二叉搜索树（BST）中查找值为 val 的节点（LeetCode 第700题：Search in a Binary Search Tree）
     *
     * 使用广度优先搜索（BFS / 层序遍历）的方式遍历整棵树，寻找目标值。
     *
     * 虽然 BST 具有有序性（左 < 根 < 右），理论上可用 O(h) 时间完成查找，
     * 但本解法采用 BFS 遍历所有可能路径，仍能正确找到目标节点。
     *
     * @param root BST 的根节点
     * @param val  要查找的目标值
     * @return 如果存在值为 val 的节点，则返回该节点；否则返回 null
     */
    public TreeNode searchBST(TreeNode root, int val) {
        // 边界情况：如果根节点为空，直接返回 null
        if (root == null) return null;
        // 创建一个队列用于层序遍历（BFS）
        Queue queue = new LinkedList<>();
        // 将根节点入队，作为遍历起点
        queue.offer(root);
        // 当队列不为空时，持续处理每一层的节点
        while (!queue.isEmpty()) {
            // 从队列中取出一个节点进行处理
            TreeNode node = queue.poll();
            // 检查当前节点的值是否等于目标值
            if (node.val == val) {
                // 找到目标节点，立即返回
                return node;
            }
            // 利用 BST 性质进行剪枝优化：
            // 如果当前节点值大于目标值，说明目标应在左子树
            if (node.val > val && node.left != null) {
                queue.offer(node.left);  // 将左子节点加入队列等待处理
            }
            // 如果当前节点值小于目标值，说明目标应在右子树
            if (node.val < val && node.right != null) {
                queue.offer(node.right); // 将右子节点加入队列等待处理
            }
            // 注意：这里没有将“错误方向”的子节点入队（如 node.val > val 时不加 right）
            // 这正是利用了 BST 的有序性，避免无效搜索，提高效率
        }
        // 遍历结束仍未找到目标值，返回 null
        return null;
    }
}