实用指南：【数据结构】带表头节点的双向链表的基本操作

一、数据结构定义

typedef struct DuLNode {
    ElemType data;           // 数据域（存储元素值）
    struct DuLNode *prior;   // 前驱指针（指向当前节点的前一个节点）
    struct DuLNode *next;    // 后继指针（指向当前节点的后一个节点）
} DuLNode, *DuLinkList;      // DuLinkList为指向节点的指针类型

• 每个节点包含 3 部分：数据域（data）、前驱指针（prior）、后继指针（next）。
• 表头节点（L）：不存储实际数据，仅用于简化操作（避免空表时的特殊处理），其prior固定为NULL，next指向首元节点（第一个有效节点）。

二、核心算法详解

1. 初始化算法（InitDuLinkList）

功能：创建表头节点，初始化双向链表为空表。步骤：

1. 为表头节点分配内存（L = new DuLNode）。
2. 检查内存分配是否成功（失败返回OVERFLOW）。
3. 初始化表头节点的指针：prior = NULL（表头无前驱），next = NULL（空表时无后继）。
4. 返回成功状态OK。

代码：

Status InitDuLinkList(DuLinkList &L) {
    L = new DuLNode;  // 分配表头节点内存
    if (!L) return OVERFLOW;  // 内存不足
    L->prior = NULL;  // 表头无前驱
    L->next = NULL;   // 空表，无首元节点
    return OK;
}

时间复杂度：O(1)（仅固定步骤操作）。

2. 查找算法（GetElem_DuL）

功能：根据位置i（1-based，从首元节点开始计数）查找节点，返回节点指针（未找到返回NULL）。步骤：

1. 从首元节点开始遍历（p = L->next，j=1作为计数器）。
2. 循环遍历：当p不为NULL且j < i时，移动p到下一个节点（p = p->next），计数器j++。
3. 终止条件：
   • 若p为NULL（已遍历到表尾，未找到第i个节点），返回NULL。
   • 若j > i（i小于 1，非法位置），返回NULL。
   • 否则，p即为第i个节点，返回p。

代码：

DuLNode* GetElem_DuL(DuLinkList L, int i) {
    int j = 1;
    DuLNode *p = L->next;  // 从首元节点开始
    while (p != NULL && j < i) {  // 遍历到第i个节点
        p = p->next;
        j++;
    }
    return (p == NULL || j > i) ? NULL : p;  // 检查合法性
}

时间复杂度：O(n)（最坏情况需遍历整个链表，n为链表长度）。边界处理：处理i < 1或i > 表长的非法情况。

3. 插入算法（ListInsert_DuL）

功能：在第i个节点之前插入新元素e。核心思路：双向链表插入需修改 4 个指针（新节点的前驱 / 后继、前驱节点的后继、后继节点的前驱），分两种场景处理。

步骤：

1. 创建新节点s，设置其数据域为e（s->data = e）。

2. 场景 1：插入到第 1 个位置（表头节点之后）：

   • 新节点s的前驱指向表头（s->prior = L）。
   • 新节点s的后继指向原首元节点（s->next = L->next）。
   • 若原链表非空（L->next != NULL），原首元节点的前驱指向s（L->next->prior = s）。
   • 表头节点的后继指向s（L->next = s），完成插入。

3. 场景 2：插入到第i（i > 1）个节点之前：

   • 调用GetElem_DuL找到第i个节点p（若p为NULL，返回ERROR）。
   • 新节点s的前驱指向p的前驱（s->prior = p->prior）。
   • p的前驱节点的后继指向s（s->prior->next = s）。
   • 新节点s的后继指向p（s->next = p）。
   • p的前驱指向s（p->prior = s），完成插入。

代码：

Status ListInsert_DuL(DuLinkList &L, int i, ElemType e) {
    DuLNode *s = new DuLNode;
    s->data = e;
    if (i == 1) {  // 插入到第1个位置（表头后）
        s->prior = L;
        s->next = L->next;
        if (L->next != NULL) L->next->prior = s;
        L->next = s;
        return OK;
    }
    DuLNode *p = GetElem_DuL(L, i);  // 找第i个节点
    if (p == NULL) return ERROR;     // i非法
    // 修改4个指针
    s->prior = p->prior;
    s->prior->next = s;
    s->next = p;
    p->prior = s;
    return OK;
}

时间复杂度：O(n)（主要耗时在查找第i个节点，i=1时为O(1)）。关键：插入时指针修改顺序不能颠倒，否则会导致链表断裂（如先修改s->prior->next，再修改p->prior）。

4. 删除算法（ListDelete_DuL）

功能：删除第i个节点。核心思路：通过修改前驱节点的后继和后继节点的前驱，断开待删除节点的链接，再释放内存。

步骤：

1. 调用GetElem_DuL找到第i个节点p（若p为NULL，返回ERROR）。
2. 修改前驱节点的后继：p->prior->next = p->next（跳过p）。
3. 若p不是最后一个节点（p->next != NULL），修改后继节点的前驱：p->next->prior = p->prior（跳过p）。
4. 释放p的内存（delete p），返回OK。

代码：

Status ListDelete_DuL(DuLinkList &L, int i) {
    DuLNode *p = GetElem_DuL(L, i);  // 找第i个节点
    if (p == NULL) return ERROR;     // i非法
    p->prior->next = p->next;  // 前驱节点跳过p
    if (p->next != NULL) {     // 若p不是最后一个节点
        p->next->prior = p->prior;  // 后继节点跳过p
    }
    delete p;  // 释放内存
    return OK;
}

时间复杂度：O(n)（主要耗时在查找第i个节点，i=1时为O(1)）。边界处理：若p是最后一个节点（p->next = NULL），无需修改后继节点的前驱（避免空指针访问）。

5. 打印算法（PrintDuLinkList）

功能：从首元节点开始，依次输出链表中所有元素。步骤：

1. 从首元节点开始遍历（p = L->next）。
2. 循环输出p->data，并移动p到下一个节点（p = p->next），直到p为NULL（表尾）。

代码：

void PrintDuLinkList(DuLinkList L) {
    DuLNode *p = L->next;
    cout << "当前双向链表元素：";
    while (p != NULL) {
        cout << p->data << " ";
        p = p->next;
    }
    cout << endl;
}

时间复杂度：O(n)（需遍历所有节点）。

三、主函数流程（算法验证）

1. 初始化链表：调用InitDuLinkList创建表头节点。
2. 插入测试：
   • 输入n个元素，均插入到第 1 个位置前（因此实际存储顺序与输入顺序相反，例如输入1 2 3，链表为3 2 1）。
   • 每次插入后输出成功信息，最后打印整个链表。
3. 删除测试：
   • 输入要删除的位置delPos，调用ListDelete_DuL删除对应节点。
   • 输出删除结果并打印修改后的链表。
4. 内存释放：遍历所有节点并释放内存（避免内存泄漏）。

四、完整代码实现

C++代码如下：

#include
using namespace std;
typedef int ElemType;
typedef int Status;
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef struct DuLNode {
    ElemType data;           // 数据域
    struct DuLNode *prior;   // 前驱指针
    struct DuLNode *next;    // 后继指针
} DuLNode, *DuLinkList;
// 函数声明
Status InitDuLinkList(DuLinkList &L);  // 初始化双向链表
DuLNode* GetElem_DuL(DuLinkList L, int i);  // 查找第i个节点
Status ListInsert_DuL(DuLinkList &L, int i, ElemType e);  // 插入元素
Status ListDelete_DuL(DuLinkList &L, int i);  // 删除元素
void PrintDuLinkList(DuLinkList L);  // 打印链表
int main() {
    DuLinkList L;
    int n, e, delPos;
    // 1. 初始化双向链表
    if (InitDuLinkList(L) != OK) {
        cout << "双向链表初始化失败！" << endl;
        return 1;
    }
    cout << "双向链表初始化成功！" << endl;
    // 2. 测试插入操作
    cout << "\n============ 测试插入操作 ============" << endl;
    cout << "请输入要插入的元素个数：";
    cin >> n;
    cout << "请依次输入" << n << "个元素（将插入到链表第1个位置前）：" << endl;
    for (int k = 1; k <= n; k++) {
        cin >> e;
        if (ListInsert_DuL(L, 1, e) == OK) {
            cout << "插入元素 " << e << " 到位置1前成功！" << endl;
        } else {
            cout << "插入元素 " << e << " 到位置1前失败！" << endl;
        }
    }
    PrintDuLinkList(L);
    // 3. 测试删除操作
    cout << "\n============ 测试删除操作 ============" << endl;
    cout << "请输入要删除的位置（1~" << n << "）：";
    cin >> delPos;
    if (ListDelete_DuL(L, delPos) == OK) {
        cout << "删除位置" << delPos << "的元素成功！" << endl;
        PrintDuLinkList(L);
    } else {
        cout << "删除位置" << delPos << "不合法或元素不存在！" << endl;
    }
    // 4. 释放内存（遍历删除所有节点和头结点）
    DuLNode *p = L->next, *q;
    while (p != NULL) {
        q = p;
        p = p->next;
        delete q;
    }
    delete L;
    return 0;
}
// 初始化双向链表（创建头结点）
Status InitDuLinkList(DuLinkList &L) {
    L = new DuLNode;
    if (!L) return OVERFLOW;
    L->prior = NULL;
    L->next = NULL;
    return OK;
}
// 查找第i个节点（返回节点指针，不存在则返回NULL）
DuLNode* GetElem_DuL(DuLinkList L, int i) {
    int j = 1;
    DuLNode *p = L->next;
    while (p != NULL && j < i) {
        p = p->next;
        j++;
    }
    return (p == NULL || j > i) ? NULL : p;
}
// 插入：在第i个节点前插入元素e（修正i=1的特殊情况）
Status ListInsert_DuL(DuLinkList &L, int i, ElemType e) {
    DuLNode *s = new DuLNode;
    s->data = e;
    // 特殊处理：插入到第一个位置（头结点之后）
    if (i == 1) {
        s->prior = L;
        s->next = L->next;
        if (L->next != NULL) {
            L->next->prior = s;
        }
        L->next = s;
        return OK;
    }
    // 插入到非第一个位置，需先找到第i个节点
    DuLNode *p = GetElem_DuL(L, i);
    if (p == NULL) return ERROR;
    // 修改4个指针完成插入
    s->prior = p->prior;
    s->prior->next = s;
    s->next = p;
    p->prior = s;
    return OK;
}
// 删除：删除第i个节点
Status ListDelete_DuL(DuLinkList &L, int i) {
    DuLNode *p = GetElem_DuL(L, i);
    if (p == NULL) return ERROR;
    // 修改前驱和后继的指针
    p->prior->next = p->next;
    if (p->next != NULL) {  // 防止最后一个节点空指针访问
        p->next->prior = p->prior;
    }
    delete p;
    return OK;
}
// 打印链表所有元素
void PrintDuLinkList(DuLinkList L) {
    DuLNode *p = L->next;
    cout << "当前双向链表元素：";
    while (p != NULL) {
        cout << p->data << " ";
        p = p->next;
    }
    cout << endl;
}

程序运行结果如下：

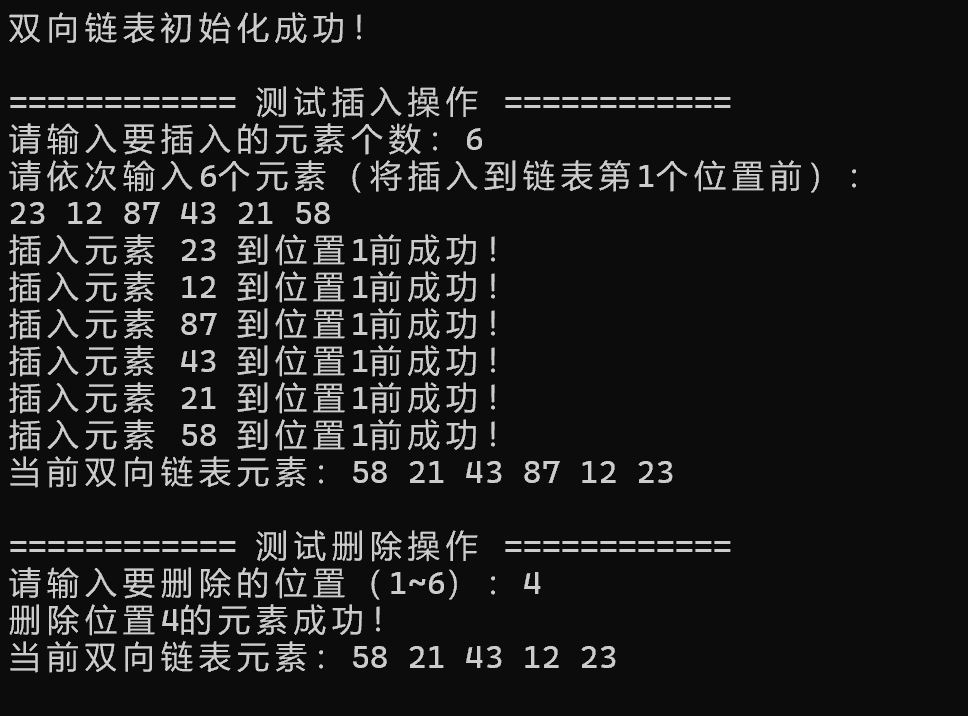
Python代码如下：

# 定义状态常量（对应原C++的宏定义）
OK = 1
ERROR = 0
OVERFLOW = -2
# 1. 双向链表节点类（对应原C++的DuLNode结构体）
class DuLNode:
    def __init__(self, data=0):
        self.data = data          # 数据域（默认值0，对应原ElemType=int）
        self.prior = None         # 前驱引用（替代指针，初始为None）
        self.next = None          # 后继引用（替代指针，初始为None）
# 2. 双向链表核心类（封装所有操作，对应原C++的函数集合）
class DoublyLinkedList:
    def __init__(self):
        self.head = None  # 链表头引用（指向表头节点，初始为空）
    def InitDuLinkList(self):
        """初始化双向链表（创建表头节点，对应原C++ InitDuLinkList）"""
        try:
            # 创建表头节点（不存储实际数据，仅用于简化操作）
            self.head = DuLNode()
            self.head.prior = None  # 表头无前驱
            self.head.next = None   # 空表时无首元节点
            return OK
        except MemoryError:
            # Python内存分配失败时触发MemoryError，对应原C++的new失败
            return OVERFLOW
    def GetElem_DuL(self, i):
        """查找第i个节点（1-based，返回节点引用；不存在返回None，对应原C++ GetElem_DuL）"""
        if self.head is None:
            return None  # 链表未初始化
        j = 1  # 计数器：从首元节点开始计数（首元为第1个节点）
        p = self.head.next  # p指向首元节点（跳过表头）
        # 遍历到第i个节点，或p为None（超出表长）
        while p is not None and j < i:
            p = p.next
            j += 1
        # 合法性判断：i<1 或 i>表长时返回None
        return p if (p is not None and j == i) else None
    def ListInsert_DuL(self, i, e):
        """在第i个节点前插入元素e（返回状态码，对应原C++ ListInsert_DuL）"""
        if self.head is None:
            return ERROR  # 链表未初始化
        # 步骤1：创建新节点
        s = DuLNode(e)
        # 场景1：插入到第1个位置（表头节点之后，首元节点之前）
        if i == 1:
            s.prior = self.head          # 新节点前驱指向表头
            s.next = self.head.next      # 新节点后继指向原首元
            # 若原链表非空，需修改原首元的前驱为新节点
            if self.head.next is not None:
                self.head.next.prior = s
            self.head.next = s            # 表头后继指向新节点（新节点成为首元）
            return OK
        # 场景2：插入到第i（i>1）个节点前：先找到第i个节点p
        p = self.GetElem_DuL(i)
        if p is None:
            return ERROR  # 第i个节点不存在（i非法）
        # 步骤2：修改4个引用，完成插入（顺序不可颠倒，避免断链）
        s.prior = p.prior        # 新节点前驱 = p的前驱
        p.prior.next = s         # p的前驱的后继 = 新节点
        s.next = p               # 新节点后继 = p
        p.prior = s              # p的前驱 = 新节点
        return OK
    def ListDelete_DuL(self, i):
        """删除第i个节点（返回状态码，对应原C++ ListDelete_DuL）"""
        if self.head is None:
            return ERROR  # 链表未初始化
        # 步骤1：找到第i个节点p
        p = self.GetElem_DuL(i)
        if p is None:
            return ERROR  # 第i个节点不存在（i非法）
        # 步骤2：修改引用，断开p的链接（处理边界：p是最后一个节点时p.next为None）
        p.prior.next = p.next  # p的前驱的后继 = p的后继
        if p.next is not None:
            p.next.prior = p.prior  # p的后继的前驱 = p的前驱
        # Python无需手动释放内存（垃圾回收自动处理无引用节点）
        return OK
    def PrintDuLinkList(self):
        """打印链表所有元素（从首元到表尾，对应原C++ PrintDuLinkList）"""
        if self.head is None:
            print("双向链表未初始化！")
            return
        p = self.head.next  # 从首元节点开始遍历
        print("当前双向链表元素：", end="")
        while p is not None:
            print(p.data, end=" ")
            p = p.next
        print()  # 换行
# 3. 主函数（测试流程，完全对应原C++ main函数）
def main():
    # 初始化双向链表
    L = DoublyLinkedList()
    if L.InitDuLinkList() != OK:
        print("双向链表初始化失败！")
        return 1
    print("双向链表初始化成功！")
    # 测试插入操作
    print("\n============ 测试插入操作 ============")
    try:
        n = int(input("请输入要插入的元素个数："))
    except ValueError:
        print("输入无效！元素个数必须为整数。")
        return 1
    print(f"请依次输入{n}个元素（将插入到链表第1个位置前）：")
    for k in range(1, n + 1):
        try:
            e = int(input(f"请输入第{k}个元素："))
        except ValueError:
            print(f"输入无效！第{k}个元素必须为整数，跳过该元素。")
            continue
        if L.ListInsert_DuL(1, e) == OK:
            print(f"插入元素 {e} 到位置1前成功！")
        else:
            print(f"插入元素 {e} 到位置1前失败！")
    L.PrintDuLinkList()
    # 测试删除操作
    print("\n============ 测试删除操作 ============")
    try:
        delPos = int(input(f"请输入要删除的位置（1~{n}）："))
    except ValueError:
        print("输入无效！删除位置必须为整数。")
        return 1
    if L.ListDelete_DuL(delPos) == OK:
        print(f"删除位置{delPos}的元素成功！")
        L.PrintDuLinkList()
    else:
        print(f"删除位置{delPos}不合法或元素不存在！")
    # Python无需手动释放内存（垃圾回收自动处理所有节点）
    return 0
# 执行主函数
if __name__ == "__main__":
    main()

程序运行结果如下：

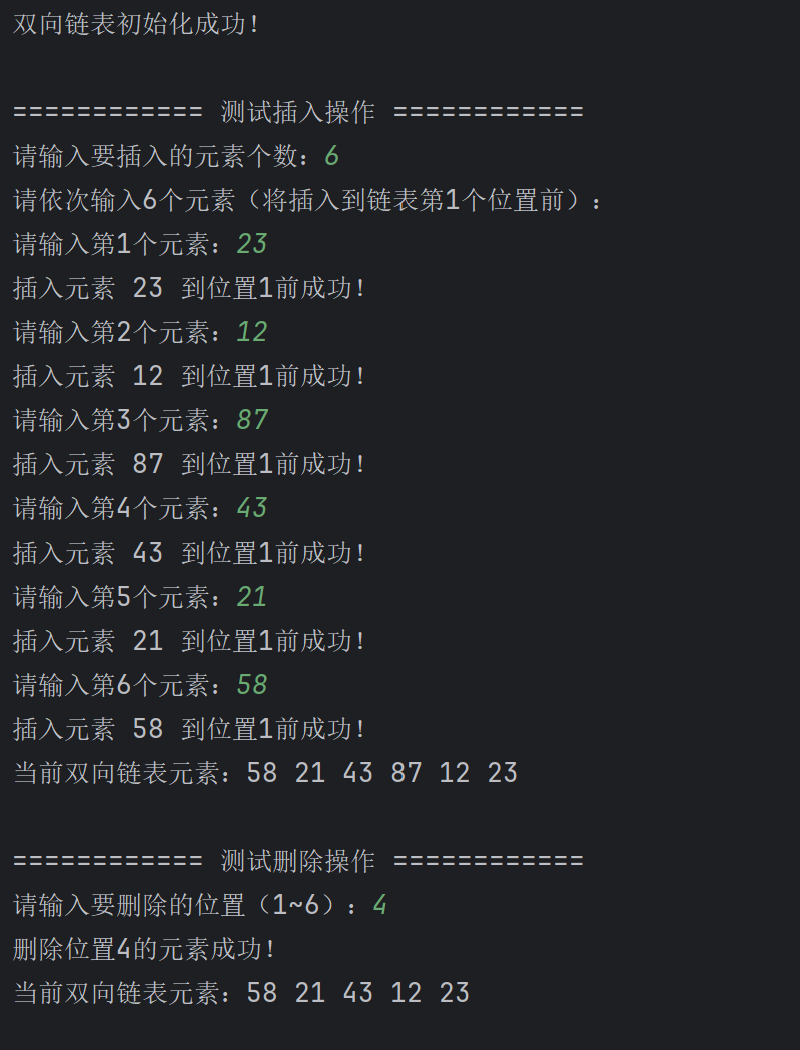
Java代码如下：

import java.util.Scanner;
// 双向链表节点类
class DuLNode {
    int data;          // 数据域
    DuLNode prior;     // 前驱节点引用
    DuLNode next;      // 后继节点引用
    // 构造器
    public DuLNode(int data) {
        this.data = data;
        this.prior = null;
        this.next = null;
    }
    // 空节点构造器（用于头节点）
    public DuLNode() {
        this(0);
    }
}
public class DoublyLinkedList {
    // 状态常量
    public static final int OK = 1;
    public static final int ERROR = 0;
    public static final int OVERFLOW = -2;
    private DuLNode head;  // 头节点引用
    // 初始化双向链表（创建头节点）
    public int initDuLinkList() {
        head = new DuLNode();
        if (head == null) {
            return OVERFLOW;
        }
        head.prior = null;
        head.next = null;
        return OK;
    }
    // 查找第i个节点（返回节点引用，不存在则返回null）
    public DuLNode getElem_DuL(int i) {
        int j = 1;
        DuLNode p = head.next;  // 从首元节点开始
        while (p != null && j < i) {
            p = p.next;
            j++;
        }
        return (p == null || j > i) ? null : p;
    }
    // 插入：在第i个节点前插入元素e
    public int listInsert_DuL(int i, int e) {
        DuLNode s = new DuLNode(e);
        // 特殊处理：插入到第一个位置（头节点之后）
        if (i == 1) {
            s.prior = head;
            s.next = head.next;
            if (head.next != null) {
                head.next.prior = s;
            }
            head.next = s;
            return OK;
        }
        // 插入到非第一个位置，先找到第i个节点
        DuLNode p = getElem_DuL(i);
        if (p == null) {
            return ERROR;
        }
        // 修改四个引用完成插入
        s.prior = p.prior;
        s.prior.next = s;
        s.next = p;
        p.prior = s;
        return OK;
    }
    // 删除：删除第i个节点
    public int listDelete_DuL(int i) {
        DuLNode p = getElem_DuL(i);
        if (p == null) {
            return ERROR;
        }
        // 修改前驱节点的后继引用
        p.prior.next = p.next;
        // 如果不是最后一个节点，修改后继节点的前驱引用
        if (p.next != null) {
            p.next.prior = p.prior;
        }
        // Java会自动回收无引用节点，无需手动释放
        return OK;
    }
    // 打印链表所有元素
    public void printDuLinkList() {
        DuLNode p = head.next;
        System.out.print("当前双向链表元素：");
        while (p != null) {
            System.out.print(p.data + " ");
            p = p.next;
        }
        System.out.println();
    }
    public static void main(String[] args) {
        DoublyLinkedList list = new DoublyLinkedList();
        Scanner scanner = new Scanner(System.in);
        int n, e, delPos;
        // 1. 初始化双向链表
        if (list.initDuLinkList() != OK) {
            System.out.println("双向链表初始化失败！");
            return;
        }
        System.out.println("双向链表初始化成功！");
        // 2. 测试插入操作
        System.out.println("\n============ 测试插入操作 ============");
        System.out.print("请输入要插入的元素个数：");
        n = scanner.nextInt();
        System.out.println("请依次输入" + n + "个元素（将插入到链表第1个位置前）：");
        for (int k = 1; k <= n; k++) {
            e = scanner.nextInt();
            if (list.listInsert_DuL(1, e) == OK) {
                System.out.println("插入元素 " + e + " 到位置1前成功！");
            } else {
                System.out.println("插入元素 " + e + " 到位置1前失败！");
            }
        }
        list.printDuLinkList();
        // 3. 测试删除操作
        System.out.println("\n============ 测试删除操作 ============");
        System.out.print("请输入要删除的位置（1~" + n + "）：");
        delPos = scanner.nextInt();
        if (list.listDelete_DuL(delPos) == OK) {
            System.out.println("删除位置" + delPos + "的元素成功！");
            list.printDuLinkList();
        } else {
            System.out.println("删除位置" + delPos + "不合法或元素不存在！");
        }
        scanner.close();
    }
}

程序运行结果如下：

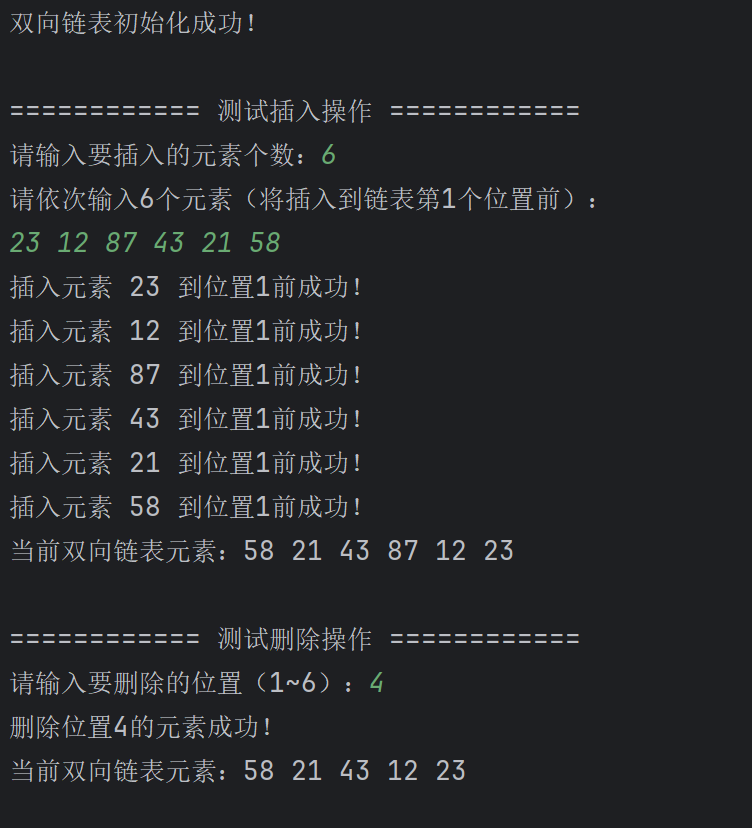
五、双向链表的优势

相比单链表，双向链表通过前驱指针prior实现了双向遍历，在以下场景更高效：

• 插入 / 删除时，无需从头遍历找前驱节点（通过p->prior直接访问）。
• 可快速反向遍历（从表尾到表头）。