动态规划day04

474. 一和零

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        //两个维度的0/1背包
        int[][] dp = new int[m + 1][n + 1];
        for (String str : strs) {
            int zeroCount = 0, oneCount = 0;
            for (char c : str.toCharArray()) {
                if (c == '0') {
                    zeroCount++;
                } else {
                    oneCount++;
                }
            }
            for (int i = m; i >= zeroCount; i--) {
                for (int j = n; j >= oneCount; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroCount][j - oneCount] + 1);
                }
            }
        }
        return dp[m][n];
    }
}

 

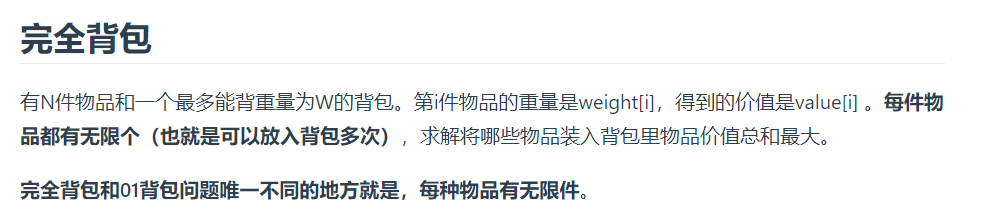
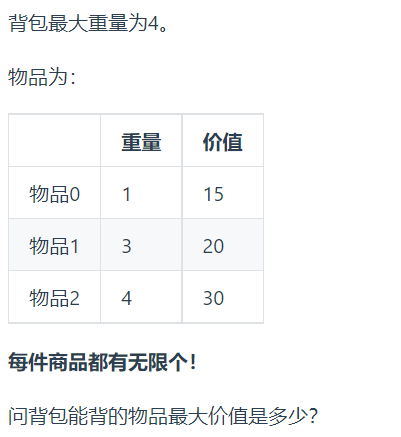
完全背包理论举例

package LeetCode;

import java.util.Arrays;

public class complete_pack {
    public static void main(String[] args) {
        int[] weight = {4, 3, 4};
        int[] value = {15, 20, 30};
        int maxWeight = 8;
        testCompletePack01(weight, value, maxWeight);
        testCompletePack02(weight, value, maxWeight);
    }

    //完全背包 二维数组
    private static void testCompletePack01(int[] weight, int[] value, int maxWeight) {
        int n = weight.length;
        int[][] dp = new int[n][maxWeight + 1];
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= maxWeight; j++) {
                dp[i][j] = Math.max(dp[i][j], dp[i][j - weight[i]] + value[i]);
            }
        }
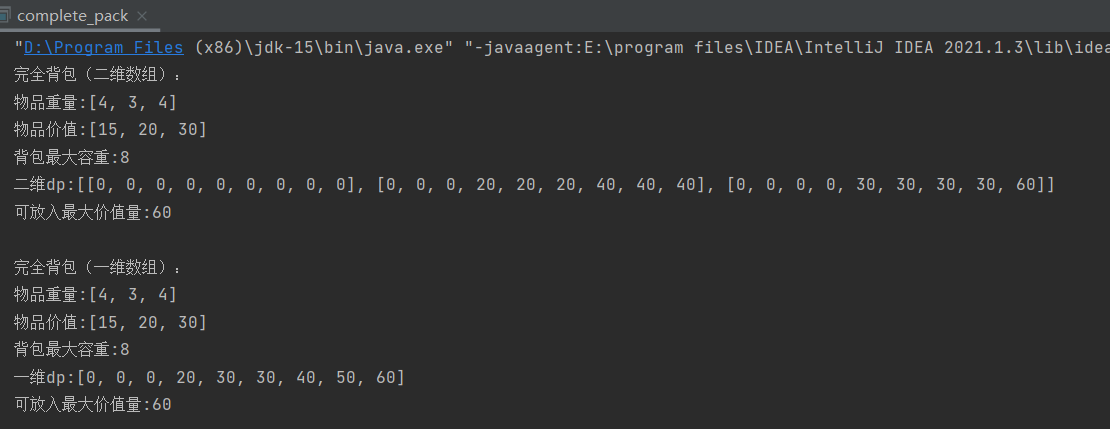
        System.out.println("完全背包（二维数组）：");
        System.out.println("物品重量:" + Arrays.toString(weight));
        System.out.println("物品价值:" + Arrays.toString(value));
        System.out.println("背包最大容重:" + maxWeight);
        System.out.println("二维dp:" + Arrays.deepToString(dp));
        System.out.println("可放入最大价值量:" + dp[n - 1][maxWeight]);
    }

    //完全背包 一位数组（先遍历物品，再遍历背包）
    private static void testCompletePack02(int[] weight, int[] value, int maxWeight) {
        int n = weight.length;
        int[] dp = new int[maxWeight + 1];
        for (int i = 0; i < n; i++) {
            for (int j = weight[i]; j <= maxWeight; j++) {
                if (j >= weight[i]) {
                    dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
                }
            }
        }
        System.out.println();
        System.out.println("完全背包（一维数组）：");
        System.out.println("物品重量:" + Arrays.toString(weight));
        System.out.println("物品价值:" + Arrays.toString(value));
        System.out.println("背包最大容重:" + maxWeight);
        System.out.println("一维dp:" + Arrays.toString(dp));
        System.out.println("可放入最大价值量:" + dp[maxWeight]);
    }
}

 

518. 零钱兑换 II

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        //金额0需要0个硬币凑是一种方法
        dp[0] = 1;
        //组合问题 在所有硬币中找凑对应金额的所有可能
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

参考： programmercarl.com