[译]Vector space model(向量空间模型)

Vector space model (or term vector model) is an algebraic model for representing text documents (and any objects, in general) as vectors of identifiers, such as, for example, index terms. It is used in information filtering, information retrieval, indexing and relevancy rankings. Its first use was in the SMART Information Retrieval System.

向量空间模型(项向量模型)是一个用来表示文本文档(通常也包含一些对象)的特征向量的数学模型,例如索引词项.它被广泛应用于信息过滤,信息检索,索引和相关度计算.最早使用向量空间模型的是SMART信息检索系统.

Clotho注: 词项(term)一般情况下就是一个词(word),特别是在文本索引领域.

 

Definitions

A document is represented as a vector. Each dimension corresponds to a separate term. If a term occurs in the document, its value in the vector is non-zero. Several different ways of computing these values, also known as (term) weights, have been developed. One of the best known schemes is tf-idf weighting (see the example below).

The definition of term depends on the application. Typically terms are single words, keywords, or longer phrases. If the words are chosen to be the terms, the dimensionality of the vector is the number of words in the vocabulary (the number of distinct words occurring in the corpus).

定义

一个文档可以表示成一个向量.一个维度相当于一个词项(term).如果一个词项出现在一篇文档中,它在向量中的值是非零的.有几种不同的计算这些被看作(词项)权重的向量值的方法被逐渐提出来.其中一种最著名的方法是tf-idf加权(看下面的例子).

词项的定义是依赖于应用的.一般而言,词项就是单字(单词),关键字,或者长短语.如果词(word)被选作词项(term),向量的维度就等于词汇表中的词数(出现在文档全集中所有不同的词的数量).

 

Applications

Relevancy rankings of documents in a keyword search can be calculated, using the assumptions of document similarities theory, by comparing the deviation of angles between each document vector and the original query vector where the query is represented as same kind of vector as the documents.

In practice, it is easier to calculate the cosine of the angle between the vectors instead of the angle:

\cos{\theta} = \frac{\mathbf{v_1} \cdot \mathbf{v_2}}{\left\| \mathbf{v_1} \right\| \left \| \mathbf{v_2} \right\|}

A cosine value of zero means that the query and document vector are orthogonal and have no match (i.e. the query term does not exist in the document being considered). See cosine similarity for further information.

应用

基于关键字检索的文档相关度计算,可以用文档相似度理论的假设来实现,就是比较每个文档向量和原始查询向量的夹角,其中查询是表示为与文档一样的向量.

(Clotho注:其实就是两个文档向量之间比较)

在实践中,计算两个向量夹角的余弦值(cosine)会比直接计算角度更简单:

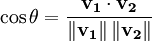
\cos{\theta} = \frac{\mathbf{v_1} \cdot \mathbf{v_2}}{\left\| \mathbf{v_1} \right\| \left \| \mathbf{v_2} \right\|}

余弦值为0时表示查询向量和文档向量之间呈直角,也就是查询和文档完全不相似(也就是查询的词项在被查询的文档中不存在).查看余弦相似度以获得更多信息.

 

Example: tf-idf weights

In the classic vector space model proposed by Salton, Wong and Yang [1] the term specific weights in the document vectors are products of local and global parameters. The model is known as term frequency-inverse document frequency model. The weight vector for document d is \mathbf{v}_d = [w_{1,d}, w_{2,d}, \ldots, w_{N,d}]^T, where

w_{t,d} = \mathrm{tf}_t \cdot \log{\frac{|D|}{|\{t \in d\}|}}

and

  • tft is term frequency of term t in document d (a local parameter)
  • \log{\frac{|D|}{|\{t \in d\}|}} is inverse document frequency (a global parameter). | D | is the total number of documents in the document set; |\{t \in d\}| is the number of documents containing the term t.

In a simpler Term Count Model the term specific weights do not include the global parameter. Instead the weights are just the counts of term occurrences: wt,d = tft.

例子: tf-idf权重

在Salton、王、杨提出的经典向量空间模型中,文档向量中词项的权重是局部参数和全局参数的乘积.该模型被认为是词频-倒文档频率模型.文档的权重向量d是\mathbf{v}_d = [w_{1,d}, w_{2,d}, \ldots, w_{N,d}]^T,

其中 w_{t,d} = \mathrm{tf}_t \cdot \log{\frac{|D|}{|\{t \in d\}|}}

在上面公式中,

* tft 是词项t在文档d中的频率(一个局部参数)

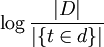* \log{\frac{|D|}{|\{t \in d\}|}}是倒文档频率(一个全局参数). | D | 是文档集合中的文档总数; 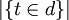|\{t \in d\}|是包含词项t的文档数.

在一个更简单的词项计算模型中,词项的权重不包括全局变量(倒文档频率),而只使用词频作为权重wt,d = tft.

 

Limitations

The vector space model has the following limitations:

  1. Long documents are poorly represented because they have poor similarity values (a small scalar product and a large dimensionality)
  2. Search keywords must precisely match document terms; word substrings might result in a "false positive match"
  3. Semantic sensitivity; documents with similar context but different term vocabulary won't be associated, resulting in a "false negative match".
  4. The order in which the terms appear in the document is lost in the vector space representation.

 

局限性

向量空间模型具有以下局限:

  1. 长篇的文档会被表示得不符合实际,因为它们只有较低的相似度值(一个小的乘积和一个大的维度数).
  2. 检索的关键字必须精确匹配文档中的词项;词素的检索可能会得到"错误肯定匹配".(Clotho注:不相似被当成相似)
  3. 语义敏感;那些拥有相似语义但使用的词汇不同的文档,会被当成"错误否定匹配".(Clotho注:相似被当成不相似)
  4. 词项在文档中的顺序会在向量空间的表示中忽略.

 

原文地址: http://en.wikipedia.org/wiki/Vector_space_model

posted @ 2009-12-30 10:10  Clotho_Lee  阅读(4234)  评论(1)  编辑  收藏  举报