LeetCode 树

认识LeetCode树的定义方式

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

94. 二叉树的中序遍历

简单的递归写法

vector <int>ans;
    vector<int> inorderTraversal(TreeNode* root) {
        dfs(root);
        return ans;

    }
    void dfs(TreeNode* root)
    {
        if(!root)return ;
        dfs(root->left);
        ans.push_back(root->val);
        dfs(root->right);
    }

迭代写法 待更

95. 不同的二叉搜索树 II

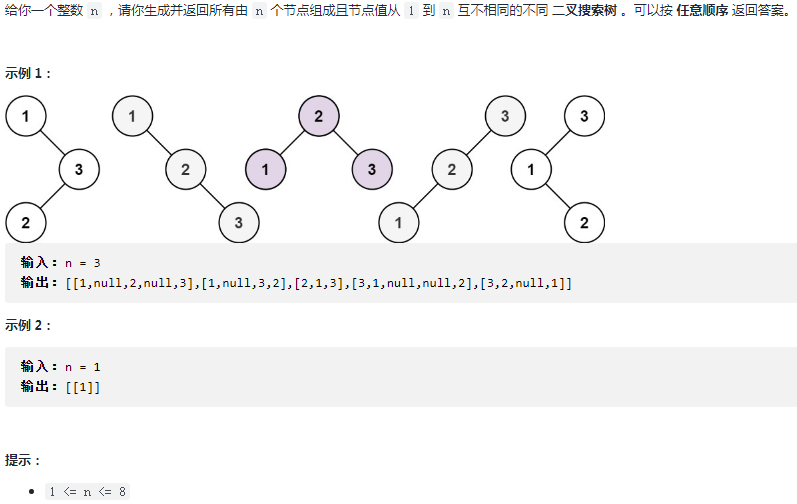
看样例发现所有中序遍历后都是1 、2 、3 、...、n的形式
当我们以k为根节点时，会不会发现 k的 左子树的编号从1到 k-1 啊，右子树 k+1 到 n 啊？
会！
所以 对于区间[l , r] 枚举根节点 k 计算出左子树 右子树 再拼上就是答案啦！

 vector<TreeNode*> generateTrees(int n) {
        return dfs(1,n);//学习自AcWing
    }
    vector<TreeNode*>dfs(int l,int r)
    {
        vector<TreeNode*>res;
        if(l>r)//说明它没有左子树或右子树咯
        {
            res.push_back(nullptr);//NULL
            return res;
        }
        for(int i=l;i<=r;i++)//子树必是连续的一段 枚举根节点i
        {
            auto left=dfs(l,i-1),right=dfs(i+1,r);//枚举 以i为根节点 所有左子树 右子树
            for(auto le: left)
            {
                for(auto ri: right)
                {
                    auto x=new TreeNode(i);//根节点 
//TreeNode(i,le,ri);
                    x->left=le,x->right=ri;
                    res.push_back(x);
                }
            }
        }
        return res;
    }

96. 不同的二叉搜索树

题意：给整数n 求节点值从 1 到 n 互不相同的二叉树有多少种
思路：
定义f[i]表示 树大小为i能构成二叉树的方案数
枚举 根节点j
f[i]等于 以1到j-1节点为子树的大小f[(j-1)-(1)+1] ,乘以j+1到i的大小f[(i)-(j+1)+1]

    int numTrees(int n) {
        vector <int >f(n+1);//长度为 i 的方案数
        f[0]=1;
        for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)//枚举根节点
        {
            f[i]+=f[j-1-1+1]*f[i-(j+1)+1];//R-L+1
        }
        return f[n];
    }

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树
思路：对每个节点找它左儿子最大值，右儿子最小值判断。

bool flag=true;
void  dfs(TreeNode* root)
{
    if(!flag)return ;
    auto p=root->left,q=root->right;
    if(p)
    {
        int l=dfsmax(p);
        if(root->val<=l)flag=false;
        dfs(p);
    }
    if(q)
    {
        int r=dfsmin(q);
        if(root->val>=r)flag=false;
        dfs(q);
    }
    
}
int  dfsmax(TreeNode* root)
{
    int res=root->val;
     auto p=root->left,q=root->right;
     if(p)res=max(res, dfsmax(p));
     if(q)res=max(res, dfsmax(q));

     return res;

}
int  dfsmin(TreeNode* root)
{
    int res=root->val;
     auto p=root->left,q=root->right;
     if(p)res=min(res, dfsmin(p));
     if(q)res=min(res, dfsmin(q));

     return res;

}
    bool isValidBST(TreeNode* root) {
       dfs(root);
        if(flag)return true;
        return false;
    }

99. 恢复二叉搜索树

 TreeNode *pre,*t1,*t2;
    void dfs(TreeNode* root)
    {
        if(!root)return ;
        dfs(root->left);
        if(pre&&pre->val>root->val)
        {
          if(!t1)t1=pre;
           t2=root;
        } 
        pre =root;
        dfs(root->right);
    }
    void recoverTree(TreeNode* root) {
        dfs(root);
        swap(t1->val,t2->val);
    }

100. 相同的树

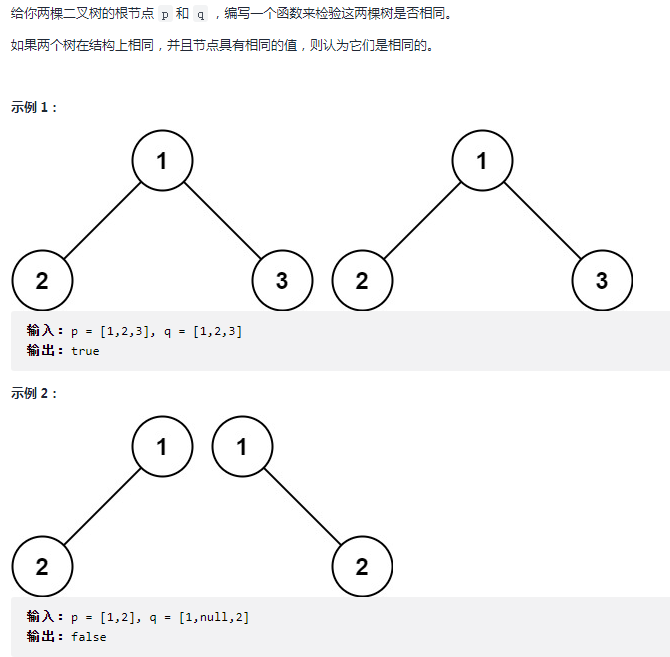
  bool isSameTree(TreeNode* p, TreeNode* q) {
        if(!p&&!q)return true;
        if(!p)return false;
        if(!q)return false;
        if(p->val!=q->val)return false;
        return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);

    }

101. 对称二叉树

思路：两个两个比较

bool isSymmetric(TreeNode* root) {
        if(!root)return true;
        return dfs(root->left,root->right);     
    }
    bool dfs(TreeNode* p,TreeNode* q)
    {
        if(!p&&!q)return true;
        if(!p||!q)return false;
        if(p->val!=q->val)return false;
        return dfs(p->right,q->left)&& dfs(p->left,q->right);
    }

102. 二叉树的层序遍历

BFS

 vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root)return {};
        int t=0;
         vector<int>w;
         vector<vector<int>>ans(10000,w);
       queue<pair<int,TreeNode*> >q;
     q.push({0,root});
     while(q.size())
     {
         auto t=q.front();
         q.pop();
         int x=t.first;TreeNode* y=t.second;
         ans[x].push_back(y->val);
         if(y->left)
         {
             q.push({x+1,y->left});
         }
          if(y->right)
         {
             q.push({x+1,y->right});
         }
     }
       

        int n=ans.size();
        for(int i=n-1;i>=0;i--)
        if(ans[i].size()==0)ans.pop_back();
            return ans;
    }

103. 二叉树的锯齿形层序遍历

把下一层的节点用vector存起来 排好后放到queue里面

void bfs(TreeNode* root, vector<vector<int>>& ans)
{
    queue<TreeNode*>q;
   
    vector <TreeNode*>a;
    int zigzag=0;
     q.push(root);
    while(q.size()||a.size())
    {
        if(q.empty())
        {
            reverse(a.begin(),a.end());
            for(auto x:a)q.push(x);
            a.clear();
            zigzag++;
            continue;
        }
        auto t=q.front();
        ans[zigzag].push_back(t->val);
        q.pop();
        auto x=t->left,y=t->right;
        if(zigzag%2==0)
        {
              if(x)a.push_back(x);
               if(y)a.push_back(y);
        }
        else 
        {
             if(y)a.push_back(y);
             if(x)a.push_back(x);
        }
    }   
}
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        if(!root)return {};
        vector<int>w;
vector<vector<int>>ans(10000,w);
        bfs(root,ans);
        int n=ans.size();
        for(int i=n-1;i>=0;i--)
        if(ans[i].size()==0)ans.pop_back();
        return ans;
    }

104. 二叉树的最大深度

int maxn=0;
void dfs(TreeNode* root,int x)
{
    maxn=max(x,maxn);
    auto p=root->left,q=root->right;
    if(p)dfs(p,x+1);
    if(q)dfs(q,x+1);
}
    int maxDepth(TreeNode* root) {
        if(!root)return 0;
        dfs(root,1);
        return maxn;
    }