假期集训Day 2 #2020011600039-46
数据结构
知识点目录
1 栈
栈:先进后出,每次加入栈顶,每次从栈顶弹出
2 队列
队列:先进先出,每次加入队尾,每次从队首弹出
双端队列
就是栈+队列
由于存在stl,所以就不仔细讲实现了
其实就是用一个指针和一个数组模拟上述过程
双端队列需要两个指针和一个数组
3 优先队列(堆)
堆是一个非常好用的东西,可以解决很多OI中的贪心问题
堆有两种,小根堆和大根堆,顾名思义,小根堆就是根最小,大根堆就是根最大
然后堆支持查询堆顶,删除堆顶
堆一般来讲,除了某些特定情况,否则均使用STL解决
堆是什么都知道吧, 主要在于快速获得全局最优解。在开启 \(O_2\) 的情况下 STL 中的任意一个堆跑出来都很快。
堆其实还支持删除堆中任意一个元素的操作,一种方法是黑书中介绍的,开启一个影射堆来映射堆中的每一个元素,但是事实上我们还有另外一种比较轻量级的解决方案。
借用标记的思想,我们维护一个和原堆同样性质(大根,小根)的堆,每次删除就把它扔到标记堆里面。当我们需要 pop 的时候,如果堆顶元素和删除堆顶元素相同,那么就说明这个元素是我们之前删除过的,于是我们就在删除堆里面和这个堆里面同时 pop, 然后考察下一元素。
容易发现时间复杂度和空间复杂度没有什么实质性的变化。
有些时候,堆不止需要删除堆顶,这个时候,我们可以通过维护两个堆来解决,一个是堆,正常即可,另外一个是标记堆,每次删除的时候,将删除的数压入标记堆,每次访问堆的时候,比较正常堆和标记堆是否相等,若相等,那么将两个的堆顶弹出即可,重复操作直到两个不相同或者标记堆为空。
4 map
5 vector
6 set
7 链表
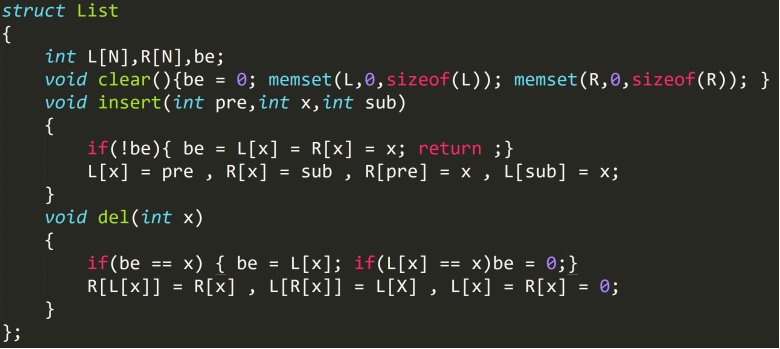
其实链表没有什么题目,或者说没有什么纯粹链表的题目
然后的话,链表分为单向链表,双向链表与双向十字链表
单向链表基本没用
双向链表可以支持\(O(1)\)插入,删除,查询前驱后继,以及\(O(n)\)查询某一项的位置
双向十字链表在dancing links中有用到
8 并查集
一种维护图上连通性的数据结构(但愿你们知道图是啥
然后的话,支持加边,和维护连通性,复杂度为\(O(log n)\)
通常实现的时候使用路径压缩,有时候可以加上启发式合并这样会将复杂度降低到\(O(alpha(n))\)级别(大概\(3\)~\(4\)左右)
然后实现很简单

有关并查集的习题,多数在最小生成树那里
然后感觉并查集的习题的话,挺容易的
其实就是这样的一个道理,每次并查集合并的时候,就相当于是把两个点的信息缩在一起了,这样就很容易理解了
9 树状数组
由于我们没讲DP,所以现在你们可以简单的用这个东西来处理,模板需要处理的内容
整体上不是很难
这是一种用于快速 (查询/修改) (前缀/后缀) 信息的数据结构
然后支持点修改
对于可以差分的信息,可以维护区间信息
然后整体就是这样
我们可以感知到的是,对于任意一个数字,我们都可以将其分拆成\(logn\)那么长的一个二进制数,所以也就是说,我们考虑通过二进制来优化维护前缀和的复杂度
我们发现,假如对于某个位置,维护这个位置二进制位中最小的那个,设为\(p = 2^k\) , 那么我们只需要维护出,所有位置,从\((x-p,x]\)这段区间的信息,然后的话,我们发现,对于任意一个位置的前缀信息都可以用\(logn\)个段表示出来,只需要将这些的贡献累加就可以了
然后考虑修改,可以发现,每次修改最多影响\(logn\)段区间
10 STL
这里说明一下若干C++中已经实现好的标准模板,也就是STL
其中vector,set,map,queue,stack这几个是比较常见的,我一一讲一下怎么用吧
1 vector
vector就是一个动态的数组
一般来说,有用的函数有resize(x),push_back(x),clear()这几个
然后是随机寻址,所以可以通过[]访问
2 queue
实现了几个简单函数
push(x),pop(),front(),empty(),size()。
3 stack
同样,也是实现了几个简单的函数
top(),push(x),pop(),size(),empty();
4 set
Set相对而言实现的功能就比较多了,并且由于他不是随机寻址,所以不能通过[]来访问其中元素,并且每次访问的时间都是\(O(log n)\)
insert(x),插入,erase(it),删除it对应的迭代器,s.find(x),返回x这个元素对应的迭代器,size()大小,empty()是否为空
然后值得一提的是,迭代器可以通过it++的形式访问第一个比这个元素大的元素,it—则是访问到第一个比它小的元素
5 map
就把这东西当成一种hash table吧
建议自行搜索
题目目录
#A P3374 【模板】树状数组 1
#B P3368 【模板】树状数组 2
#C P1044 栈
#D P1198 [JSOI2008]最大数
#E P3252 [JLOI2012]树
#F P1168 中位数
#G P3503 [POI2010]KLO-Blocks
#H P3545 [POI2012]HUR-Warehouse Store
1 树状数组 LGP3374
2020011600039
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
//#define lowbit(i) i&(-i)
using namespace std;
int n,m;
int p[500005],a[500005];
int lowbit(int i){
return i&(-i);
}
void changex(int num,int h){
for(int i=num;i<=n;i+=lowbit(i)){
a[i]+=h;
}
return ;
}
int findx(int x){
int sum=0;
for(int i=x;i;i-=lowbit(i)){
sum+=a[i];
}
return sum;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&p[i]);
}
for(int i=1;i<=n;i++){
changex(i,p[i]);
}
while(m--){
int b=0,x=0,y=0;
scanf("%d%d%d",&b,&x,&y);
if(b==1){
changex(x,y);
}
if(b==2){
printf("%d\n",findx(y)-findx(x-1));
}
}
return 0;
}
2 树状数组 2 LGP3368
2020011600040
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m;
int z[500005],a[500005],p[500005];
int lowbit(int i){
return i&(-i);
}
void changex(int num,int h){
for(int i=num;i<=n;i+=lowbit(i)){
a[i]+=h;
}
return ;
}
void addd(int x,int y,int z){
changex(x,z);
changex(y+1,-z);
return ;
}
int findx(int x){
int sum=0;
for(int i=x;i;i-=lowbit(i)){
sum+=a[i];
}
return sum;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&p[i]);
}
z[1]=p[1];
for(int i=2;i<=n;i++){
z[i]=p[i]-p[i-1];
}
for(int i=1;i<=n;i++){
changex(i,z[i]);
}
while(m--){
int b=0,x=0,y=0,z=0;
scanf("%d",&b);
if(b==1){
scanf("%d%d%d",&x,&y,&z);
addd(x,y,z);
}
if(b==2){
scanf("%d",&x);
printf("%d\n",findx(x));
}
}
return 0;
}
3 最大数[BZOJ1012][JSOI2008]LGP1198
2020011600041
题意描述
现在请求你维护一个数列,要求提供以下两种操作:
1、查询操作。语法:Q L 功能:查询当前数列中末尾 \(L\) 个数中的最大的数,并输出这个数的值。保证 \(L\) 不超过当前数列的长
度。
2、插入操作。语法:A n 功能:将 \(n\) 加上 \(t\),其中 \(t\) 是最近一次查询操作的答案(如果还未执行过查询操作,则 \(t=0\)),并将所得结果对一个固定的常数 \(D\) 取模,将所得答案插入到数列的末尾。保证 \(n\) 是非负整数并且在 int 内。
注意:初始时数列是空的,没有数字。
操作数 \(S \leq 2 \times 10^5\)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
inline ll read(){
char ch=getchar();ll sum=0,f=1;
while(ch<'0'||ch>'9'){
ch=getchar();
if(ch=='-') f=-1;}
while(ch>='0'&&ch<='9')
sum*=10,sum+=ch-'0',ch=getchar();
return sum*f;
}
const int N=200005;
ll m,MO,t;
ll stack[2][N],top,cnt;
void add(int k){//添加元素
cnt++;
while(k>stack[1][top]&&top>0) top--;
stack[0][++top]=cnt;
stack[1][top]=k;
}
void query(int emm,int l,int r){//查询
while(l<r){
int mid=(l+r)/2;
if(stack[0][mid]<emm) l=mid+1;
else r=mid;
}t=stack[1][r];
printf("%lld\n",t);
}
int main()
{
m=read(),MO=read();
while(m--){
char ch=getchar();
while(ch!='A'&&ch!='Q') ch=getchar();
if(ch=='A') add((t+read())%MO);
else query(cnt-read()+1,1,top);
}
}
题解
线段树显然可做,但是我们来思考一些更简单的做法
显然一个数如果右面有比他还大的数, 那他永远都不可能成为答案了
维护一个单调递减的栈, 每次二分查询即可
显然不能使用STL的栈,因为这道题需要我们访问栈内元素
这个做法应该是…….用单调栈把问题转化成一个二分答案题
简解:
先开两个栈。第一个栈存储在队列里的位置,第二个栈存储这个数字的大小
每当有新元素要入队的时候,我们可以把排在这个元素前的比它小的数直接忽略了(因为查询的区间永远都是后L个数,所以...)然后更新一下两个栈。
接下来我们就可以二分栈的下标,直到二分到一个下标i,使stack[2][i]表示的队列位置在所求的区间里,那么答案就有了。
4 树 [JLOI2012] LGP3252
2020011600042
题意描述
给定一个值 \(S\) 和一棵树。在树的每个节点有一个正整数,问有多少条路径的节点总和为 \(S\) 。路径中节点的深度必须是升序的。假设节点 \(1\) 是根节点,根的深度是 \(0\),它的儿子节点的深度为\(1\)。路径不必一定从根节点开始。
题解
DFS 一遍整颗树
当便利到一个点时将这个点加入队列,同时队头向 后调整,使队列中元素之和 \(<les\) 记录 \(ans\)
当一个点出栈时将队尾删除,同时队头向前调整,使队列中元素之和刚好 \(\leq s\)
显然需要使用双端队列
5 Blocks [bzoj2086][Poi2010] LGP3505
2020011600043
题意描述
给出 N 个正整数 a[1..N],再给出一个正整数 k,现在可以进行如下操作:
每次选择一个大于 k 的正整数 \(a[i]\),将 \(a[i]\) 减去 \(1\),选择\(a[i-1]\) 或 \(a[i + 1]\) 中的一个加上 \(1\)。经过一定次数的操作后,问最大能够选出多长的一个连续子序列,使得这个子序列的每个数都不小于 \(k\)。
总共给出 \(M\) 次询问,每次询问给出的\(k\) 不同,你需要分别回答。
\((N \leq 1000000,M \leq 50,k \leq 10^9)\)
保证答案都在 long long 以内
题解
显然一段的平均数超过 \(k\) 即是合法解,将 \(a[i]\) 减去 \(k\),求其前缀和。 \(i > j\) 且 \(sum[i]\geq sum[j]\) 则 \(j\) 作为左端点比 \(i\) 更优,所以只要先维护一个 \(sum\) 的单调递减栈,再用一个指针从 \(n\) → \(0\) 扫一下,不断弹栈,更新答案。
6 钓鱼
2020011600044
题意描述
有一行池塘在一条直线上,每个池塘里面最开始有 \(c_i\) 条鱼,从起点到第 \(i\) 个池塘需要走 \(dis_i\) 的时间。
现在你可以在第 \(i\) 个池塘钓鱼,然后第 \(i\) 个池塘会减少 \(p_i\) 条鱼(最少是 \(0\)),从起点出发,最后走到距离起点最远的一个池塘,可以在中途钓鱼,并且在 \(lmt\) 时间内最多能获得多少条鱼?(\(n \leq 105\))
题解
显然是不需要走回头路的。我们可以先从 \(lmt\) 时间内扣掉从头走到尾的时间,然后就可以忽略在池塘间移动的时间。剩下的问题就是一个简单的堆贪心了。
7 Warehouse Store[POI2012] LGP3545
2020011600045
题意描述
有一家专卖一种商品的店,考虑连续的 \(n\) 天。第 \(i\) 天上午会进货 \(A_i\) 件商品,中午的时候会有顾客需要购买\(B_i\) 件商品,可以选择满足顾客的要求,或是无视掉他。如果要满足顾客的需求,就必须要有足够的库存。问最多能够满足多少个顾客的需求。
题解
我们最先想到的是能卖就卖,但是却有可能直接卖给一个人剩下的不够而 GG
为了避免这种情况,我们可以这样,我们把卖掉的所有价值扔到一个堆里,每次取出堆顶的元素和当前的价值进行比较,如果堆顶的元素比他大而且把堆顶元素加上可以买这个东西,那就“退掉”之前的东西,换给他。
这样虽然不能使答案增加,但是可以增加库存。有一种前人栽树后人乘凉的感觉 233
8 中位数[POJ3784]LGP1168
2020011600046
题意描述
给出一个长度为\(N\)的非负整数序列A_i,对于所有\(1\leq k \leq \dfrac{N+1}{2}\),输出\(A_1, A_3, ..., A_{2k - 1}\)的中位数。即前\(1,3,5,...\)个数的中位数。
输入
第1行为一个正整数\(N\),表示了序列长度。
第2行包含\(N\)个非负整数\(A_i (A_i \leq 10^9)\)
输出
共\(\dfrac{N+1}{2}\)行,第\(i\)行为\(A_1,A_3,..., A_{2k - 1}\)的中位数。
#include<bits/stdc++.h>
#include<queue>
using namespace std;
int n;
int a[100100];
int mid;
priority_queue<int> q1;//大根堆
priority_queue<int,vector<int>,greater<int> >q2;//小根堆
int main(){
scanf("%d",&n);
scanf("%d",&a[1]);
mid=a[1];
printf("%d\n",mid);//mid初值是a[1]
for(int i=2;i<=n;i++){
scanf("%d",&a[i]);
if(a[i]>mid) q2.push(a[i]);
else q1.push(a[i]);
if(i%2==1){//第奇数次加入
while(q1.size()!=q2.size()){
if(q1.size()>q2.size()){
q2.push(mid);
mid=q1.top();
q1.pop();
}
else{
q1.push(mid);
mid=q2.top();
q2.pop();
}
}
printf("%d\n",mid);
}
}
return 0;
}
题解
一组数按顺序加入数组,每奇数次加入的时候就输出中位数考虑维护两个堆,一个大根堆一个小根堆,每次插入后维持两个堆的平衡即可。
这个东西其实叫对顶堆。
使用两个堆,大根堆维护较小的值,小根堆维护较大的值,即小根堆的堆顶是较大的数中最小的,大根堆的堆顶是较小的数中最大的,将大于大根堆堆顶的数(比所有大根堆中的元素都大)的数放入小根堆,小于等于大根堆堆顶的数(比所有小根堆中的元素都小)的数放入大根堆,那么就保证了所有大根堆中的元素都小于小根堆中的元素。于是我们发现对于大根堆的堆顶元素,有【小根堆的元素个数】个元素比该元素大,【大根堆的元素个数-1】个元素比该元素小;同理,对于小跟堆的堆顶元素,有【大根堆的元素个数】个元素比该元素小,【小根堆的元素个数-1】个元素比该元素大;那么维护【大根堆的元素个数】和【小根堆的元素个数】差值不大于1之后,元素个数较多的堆的堆顶元素即为当前中位数;(如果元素个数相同,那么就是两个堆堆顶元素的平均数,本题不会出现这种情况)。根据这两个堆的定义,维护方式也很简单,把元素个数多的堆的堆顶元素取出,放入元素个数少的堆即可。使用了STL的优先队列作为堆。
首先记录一个变量\(mid\),记录答案(中位数)。建立两个堆,一个大根堆一个小根堆,大根堆存\(\leq mid\)的数,小根堆存\(>mid\)的的数。所以我们向堆中加入元素时,就通过与\(mid\)的比较,选择加入哪一个堆
scanf("%d",&a[i]);
if(a[i]>mid) q2.push(a[i]);
else q1.push(a[i]);
显然,小根堆的堆顶是第一个大于\(mid\)的数,大根堆堆顶是第一个小于等于\(mid\)的数字。 但是我们在输出答案前需要对\(mid\)进行调整,如果小根堆和大根堆内元素相同,就无需处理,此时\(mid\)仍然是当前的中位数。如果两个堆中元素个数不同,那我们就需要进行调整。 具体是把元素个数较多的堆的堆顶作为\(mid\),\(mid\)加入元素较少的堆。
if(q1.size()>q2.size()){
q2.push(mid);
mid=q1.top();
q1.pop();
}
同理,如果\(q_2\)中元素比\(q_1\)多,同理转移。最后,在奇数个元素加入时输出此时的中位数\(mid\)即可。
如何动态维护一个集合的中位数
维护两个堆,一个大根堆,一个小根堆,大根堆里存储小于等于中位数的部分,不超过\([\dfrac{n}{2}]\)个,小根堆则储存大于等于中位数的部分,同样不超过\([\dfrac{n}{2}]\)个。
然后的话,每次加入一个数的时候,考虑是否比中位数大,然后对两个堆进行调整即可


 浙公网安备 33010602011771号
浙公网安备 33010602011771号