假期集训Day 1 #2020011600028-38
搜索
第一天集训,全程一脸懵...还要继续加油!搜索这部分(自认为)比较难理解,所以还是要多做题多思考。
知识点目录
1 深度优先搜索(DFS)
基本思想
为了求得问题的解,先选择某一种可能情况向前(子结点)探索,在探索过程中,一旦发现原来的选择不符合要求,就回溯至父亲结点重新选择另一结点,继续向前探索,如此反复进行,直至求得最优解。深度优先搜索的实现方式可以采用递归或者栈来实现。
复杂度的计算
复杂度分为两个部分,一部分是状态数,一部分是扩展后继状态的复杂度
所以要想优化搜索,要么减小状态数,要么减小扩展后继的计算量
实现框架
void dfs(int dep, int n)
{
if(dep == n)
{
}
for(int j =1; j <= n; j++)
{
if(is_used[j] != 1)
{
is_used[j] = 1;
dfs(dep + 1, n);
is_used[j] = 0;
}
}
}
2 广度优先搜索(BFS)
深度优先搜索(DFS):用来求最优值,我们通常不知道最优答案在哪一层,比较耗时。
queue Q;
Q.push( startState );
While ( ! Q.empty ) {
curState = Q.front();
if( curState == endState ) return true;
mark[curState] = true;
extState = extend ( curState );
If( !mark[extState] ) {
Q.push( extState );
}
}
3 迭代加深搜索(IDDFS)
用 DFS 去模拟 BFS 的过程
限制深度的 DFS 搜索,减小了空间的消耗
定义:
迭代加深搜索是在速度上接近广度优先搜索,空间上和深度优先搜索相当的搜索方式。由于在使用过程中引入了深度优先搜索,所以也可以当作深度优先搜索的优化方案。
迭代加深搜索适用于当搜索深度没有明确上限的情况。
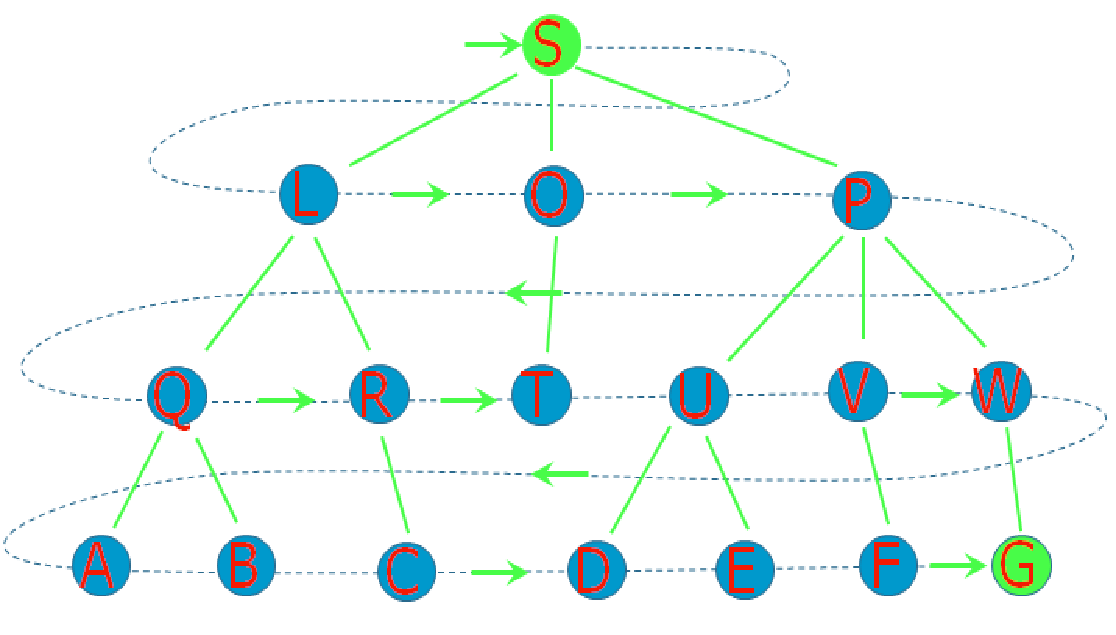
例如下图的一棵搜索树,在进行深度优先搜索前先规定好这次搜索的最大深度dep,当搜索到达dep却还没搜索到结果时回溯。之后不断加大搜索深度,重新搜索,直到找到结果为止。虽然这样搜索次数会累计很多次,但每一次搜索的范围和下一次搜索的范围相比微不足道,所以整体搜索速度不会受太大影响。
由于深度是从小到大逐渐增大的,所以当搜索到结果时可以保证搜索深度是最小的。这也是迭代加深搜索在一部分情况下可以代替广度优先搜索的原因(还比广搜省空间)。

算法:
假设G是需要搜索到的结果。
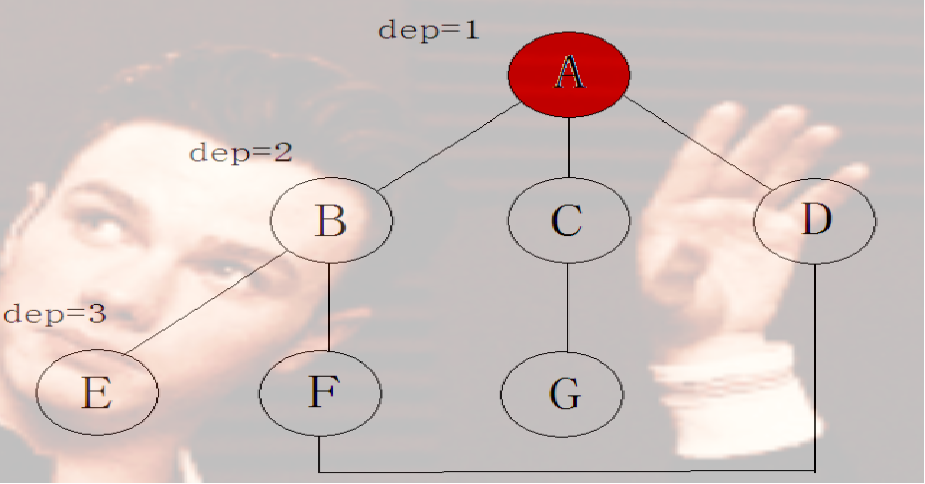
当 dep = 1 时搜索深度为1,搜索到节点 A,未搜索到结果,dep++ 并进行下一次深搜
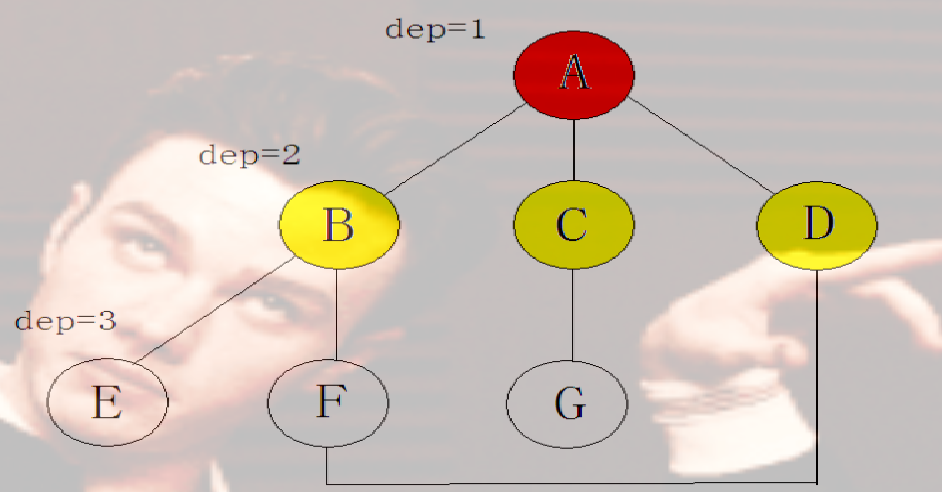
当 dep = 2 时搜索深度为2,搜索到节点 A,B,C,D 未搜索到结果,dep++ 并进行下一次深搜。
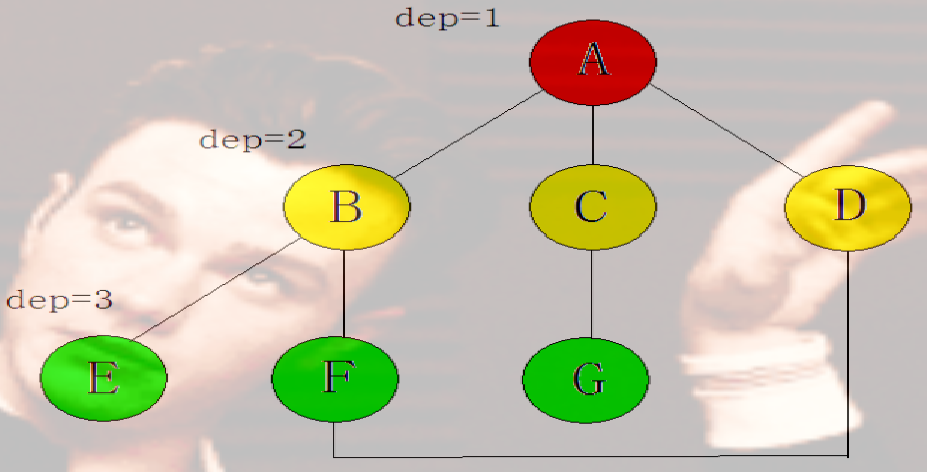
当 dep = 3 时搜索深度为3,搜索到节点 A,B,C,D,E,G 搜索到结果G,停止全部搜索并记录记录结果。
4 双向广度搜索
每次扩展不仅扩展起始节点端,同时扩展终点端的搜索状态,直到中途相遇
定义:
如果已经知道搜索的开始状态和结束状态,要找一个满足某种条件的一条路径(一般是最短路径),为了避免无谓的“组合爆炸”产生,就可以采取双向广度搜索算法,也就是从开始状态和结束状态同时开始搜索,一个向前搜,一个向后找。
这样做的好处是什么?
我们不妨假设每次搜索的分支因子是\(r\),如果最短的路径长为\(L\)的话(也就是搜了\(L\)层),那么,用一般的BFS算法(不考虑去掉重复状态),总的搜索状态数是\(r^L\);而如果采取双向BFS算法,那么,从前往后搜,我们只需要搜索\(\dfrac{L}{2}\)层,从后往前搜,我们也只要搜\(\dfrac{L}{2}\)层,因此,搜索状态数是\(2\times r^{\dfrac{L}{2}}\),比普通BFS就快了很多了。
双向BFS算法的实质还是BFS,只不过两边同时开始BFS而已。还是可以利用队列来实现:可以设置两个队列,一个用于向前的BFS,另一个用于向后的BFS,利用这两个队列,同时从前、后开始层次遍历搜索树。
5 基本数据结构(栈与队列)
题目目录
1 全排列 LGP1706
2020011600028
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int a[25];
bool vis[25];
int n;
int ans=0;
void dfs(int x){
if(x==n+1){
for(int i=1;i<=n;i++){
printf("%d ",a[i]);
}
printf("\n");
return;
}
for(int i=1;i<=n;i++)
{
if(vis[i]==1) continue;
vis[i]=1;
a[x]=i;
dfs(x+1);
vis[i]=0;
}
return ;
}
int main( ){
scanf("%d",&n);
dfs(1);
return 0;
}
2 八皇后 LGP1219
2020011600029
八皇后
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int a[25];
bool vis[25];
int n;
int ans=0;
void f(int x){
if(x==n+1){
ans++;
if(ans<=3){
for(int i=1;i<=n;i++){
printf("%d ",a[i]);
}
printf("\n");
}
return;
}
for(int i=1;i<=n;i++)
{
if(vis[i]==1) continue;
bool q=1;
for(int j=1;j<x;j++)
{
if(abs(x-j)==abs(i-a[j])){
q=0;
break;
}
}
if(q){
vis[i]=1;
a[x]=i;
f(x+1);
vis[i]=0;
}
}
return ;
}
int main( ){
scanf("%d",&n);
f(1);
printf("%d",ans);
return 0;
}
\(n\)皇后
在一个 \(n\times n\) 的国际象棋棋盘上放置\(n\)个皇后,使得它们中任意 2 个之间都不互相“攻击”,即任意 2 个皇后不可在同行、同列、同斜线上。求 \(N\) 皇后问题的所有放法。
输入 \(n\),每行输出一种方案,每种方案顺序输出皇后所在的列号,各个数之间用空格隔开。
输入
4
输出
2 4 1 3 3 1 4 2
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int m,d[15],b[15],found=0,n;
bool place(int x)//判断第 x 行的 d[x]列是否可以放置皇后
{
for(int i=1;i<x;i++)
if ((abs(d[i]-d[x])==abs(i-x))||(d[i]==d[x])) return false;
return true;
}
void print() {
found=1;
for(int i=1;i<=n;i++) printf("%d ",d[i]);
printf("\n");
}
void dfs(int x) //表示第 x 行
{
for(int i=1;i<=n;i++) //选择列
{
d[x]=i;
if (place(x)) //如果第 x 行的第 i 列可以放置皇后
{
if (x==n) print(); //最后一行放置成功,则输出答案 else dfs(x+1); //继续放置下一行
}
}
}
int main() {
int i,j;
scanf("%d",&n);
dfs(1);
if(found==0) printf("no solute!");
return 0;
}
3 生日蛋糕 LGP1731 [NOI1999]
2020011600030
题意描述
做一个生日蛋糕,生日蛋糕是由 \(m\)个圆柱体构成的,且满足以下条件
- 从下往上,圆柱半径和高都越来越小
- 总体积为 \(n\)
求表面积最小的蛋糕制作方案(底面不算表面积)
题解
什么规律也没有,貌似只能搜索了
用什么表示状态?
\((i, H_i, R_i, V_i, S_i)\) 表示第 \(i\) 层,高度为 \(H_i\),半径为 \(R_i\),已用体积为 \(V_i\),当前表面积为\(S_i\)
可惜这样的算法是不能通过的,我们要考虑剪枝
最优化剪枝:如果当前已用表面积加上余下最小的侧面积大于已知最优解,剪枝
可行性剪枝:剩下的材料太多或太少,做不了恰好剩下的层数,剪枝
4 LGP1379 八数码难题
2020011600031
题意描述
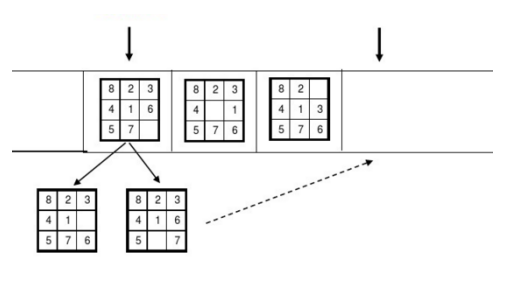
有一块 3 × 3 板子,上面有 8 个空格分别写着 1 到 8 的 8 个数,有一个格子为空格,每次可以选择空格与周围某个数字格交换,问最少多少步可以移动成最后一个格为空格,其余格为 1 到 8顺次排列的状态
#include <cstdio>
#include<map>
#include<queue>
#include<algorithm>
#define ll long long
using namespace std;
const ll dx[]={-1,0,0,1},dy[]={0,-1,1,0};
ll n;
bool check(int nx,int ny){
return(nx<0||ny<0||nx>2||ny>2);
}
int main()
{
scanf("%lld",&n);
queue<ll> q;
q.push(n);
map<ll,ll> m;
m[n]=0;
while(!q.empty())
{
int u=q.front();
int c[3][3],f=0,g=0,n=u;q.pop();
if(u==123456780)break;
for(ll i=2;i>=0;i--)
for(ll j=2;j>=0;j--)
{
c[i][j]=n%10,n/=10;
if(!c[i][j])f=i,g=j;
}
for(ll i=0;i<4;i++)
{
ll nx=f+dx[i],ny=g+dy[i],ns=0;
if(check(nx,ny))continue;
swap(c[nx][ny],c[f][g]);
for(ll i=0;i<3;i++)
for(ll j=0;j<3;j++)ns=ns*10+c[i][j];
if(!m.count(ns))
{
m[ns]=m[u]+1;
q.push(ns);
}
swap(c[nx][ny],c[f][g]);
}
}
printf("%d",m[123456780]);
return 0;
}
题解
首先我们已知原始状态,先把原始状态压入队列
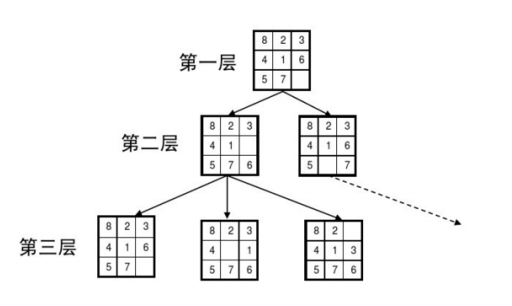
接着我们每次有几个扩展,每次取出队头状态扩展后,把新扩展的且未出现过的几个状态压入队列,同时记录每个状态的深度
然后把新的状态压入队列
状态怎么存?
一共有 9! 状态,我们可以预先设计一种规则来表示,把一个棋盘状态映射成一个数字
判重则只需要一个数组即可
5 倒牛奶 LGP1215(USACO1.4)
2020011600032
题意描述
有三个桶,容量分别为 \(a, b, c\) 升
一开始 \(A\) 桶没有水,\(B\) 桶也没有水,\(C\) 桶水是满的
每次可以把一个桶里的水倒入另一个桶,直到桶被灌满或者桶空了
求 \(A\) 桶空了的时候,\(C\) 桶的水可能是几升
\(a, b, c \leq 20\)
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
int a,b,c;
bool vis[25][25][25];
int k=0,ans[100];
void dfs(int va,int vb,int vc){
if(vis[va][vb][vc]) return ;
if(va==0){
k++;
ans[k] = vc;
}
vis[va][vb][vc] = 1;
if(vc){
if(va<a) dfs(min(a,va+vc),vb,vc-(min(a,va+vc)-va));
if(vb<b) dfs(va,min(vb+vc,b),vc-(min(b,vb+vc)-vb));
}
if(vb){
if(va<a) dfs(min(a,va+vb),vb-(min(a,va+vb)-va),vc);
if(vc<c) dfs(va,vb-(min(c,vc+vb)-vc),min(c,vc+vb));
}
if(va){
if(vc<c) dfs(va-(min(c,va+vc)-vc),vb,min(c,vc+va));
if(vb<b) dfs(va-(min(b,va+vb)-vb),min(b,va+vb),vc);
}
return ;
}
int main(){
scanf("%d%d%d",&a,&b,&c);
dfs(0,0,c);
sort(ans+1,ans+k+1);
for(int i=1;i<=k;i++) printf("%d ",ans[i]);
return 0;
}
题解
每次有 \(6\) 种选择,直接搜索即可
用一个数组判断是否搜到重复状态
\(vis_{a,b}\) 表示 \(A\) 桶中\(a\) 升水,\(B\) 桶中 \(b\) 升水这个状态是否已经搜过了
6 骑士问题
2020011600033
题意描述
在一个 \(n\times n\) 的棋盘中摆放尽量少的骑士(类似中国象棋中的马,但没有蹩马腿的规则),使得棋盘的每一格都会被至少一个骑士攻击到。但是骑士无法攻击到它自己站的位置。
另一版本
在一个标准8×8的国际象棋棋盘上,棋盘中有些格子是可能有障碍物的。已知骑士的初始位置和目标位置,你的任务是计算出骑士最少需要多少步可以从初始位置到达目标位置。有障碍物的格子当然不可能到达。
标准的8×8的国际象棋棋盘中每一个格子可以用唯一的编号确定。行用1~8这8个数字依次表示,列用“a”~“h”这8个字母依次表示。例如下图(a)的骑士所在位置(图中有n的格子)的编号为“d4”(注意“d”和“4”之间没有空格),我们知道国际象棋中的骑士可以按“L”路线移动(一个方向走2个格子,接着垂直方向走一个格子)。因此,如图(a)所示的骑士(位于d4),可以到达位置c2,b3,b5,c6,e6,f5,f3和e6,e2(图中有“x”标记的格子)。此外,骑士不能移出棋盘。

骑士可以按照移动规则自由地在棋盘上没有障碍物的格子中移动。图b给出了一个骑士移动的例子,也就是输入样例中第一组数据对应的例子。
初始格子用“n”标记,目标格子用“N”标记,有障碍物的格子用“b”标记。一个可行的移动序列在图中用数字标记出来(a1,b3,a5,c6,e5,g4,h2,f1)。总共需要7步才能完成。事实上,这也是最少的步数了。

题解
求最小,用广度优先搜索
每次扩展状态之后把状态放入尾部,然后记录每个状态摆放了多少个骑士,如果发现某个状态合法,那就说明这就是答案了
1 process(state)
2 for each possible next state from this one
3 enqueue next state
4 search()
5 enqueue initial state
6 while !empty(queue)
7 state = get state from queue
8 process(state)
状态去重?
不用考虑去重的问题,因为不会出现重复
有初始目标和结束目标我们通常想到的算法就是BFS。
7 埃及分数
2020011600034
题意描述
给一个分数,求最少用几个分母不重复且分子等于 1 的分数的和能表示出来。分数最少的同时,要求最小的分数尽量大,然后次小的分数尽量大等等


#include<bits/stdc++.h>
#define ll long long
using namespace std;
int lim,ans;
bool flag;
int num[1010],tot[1010];
void dfs(ll dep,ll mol,ll den,ll pre) //dep(搜索深度),mol(分子),den(分母),pre(上一个分母)
{
if(dep==lim+1)
{
if(mol==0)
{
flag=true;
if(num[lim]<tot[lim])
{
for(ll i=1;i<=lim;i++)
tot[i]=num[i];
ans=num[lim];
}
}
return;
}
if((den*(lim+1-dep))/mol>ans||num[dep]>ans)return;
for(ll i=max(pre,den/mol);i<=den*(lim+1-dep)/mol;i++)
{
num[dep]=i;
dfs(dep+1,mol*i-den,den*i,i+1);
}
}
int main()
{
int a,b;
cin>>a>>b;
for(lim=1;;lim++)
{
tot[lim]=0x3f3f3f3f;
ans=0x3f3f3f3f;
dfs(1,a,b,1);
if(flag)break;
}
for(ll i=1;i<lim;i++)
{
cout<<tot[i]<<" ";
}
cout<<tot[lim]<<endl;
return 0;
}
题解
此题最大的问题在于,如果使用 BFS 状态数非常大,很有可能队列不够大,超出内存限制
使用限制深度的 DFS 搜索,枚举最大深度,就可以得到结果了
如果剩下的分数都用最大的还不能在深度限制内凑出原分数,剪枝
把原分数分解成的分数个数\(K\)为层数,从一开始的状态按照分母从小到大的顺序搜索。若在某一层搜到了解并且这一层已经搜完了,那这一层的最优解一定是整个问题的最优解。
假设现在要分解的分数是\(\dfrac{a}{b}\);
若当前原分数已经分解成为超过\(K\)个分数,直接返回即可。
若\(a\)能整除\(b\),那分解结束了,最后一个分母是\(\dfrac{a}{b}\)。用当前的解去更新答案,如果没有答案或当前解包含的分母个数少于答案或当前解包含的分母个数等于答案且当前解的最大分母比答案大,则当前解即为答案。
否则,要枚举\(i\),使得\(\dfrac{a}{b}=\dfrac{a'}{b'}+\dfrac{1}{i}\),使\(i\)作为当前解的一部分,进入下一层递归。
\(i\)的范围如何确定?首先\(i\)要大于等于\([\dfrac{a}{b}]\),只有这样,才能使\(\dfrac{a}{b}\geq \dfrac{1}{i}\),这样的\(i\)才满足题意;其次\(i\)要大于当前解中分母最大的元素,这是搜索顺序决定的。同时\(i\)的值不能太大,要满足当前的分数有能分解成\(K\)个以内分数的可能性,假设\(i\)作为第\(step\)个分母,那么第\(step+1\)到第\(K\)个分母都应大于\(i\),这些分数的和小于\(\dfrac{K-step}{i}\),要有解,则必须\(\dfrac{1}{i}+\dfrac{K-step}{i}=\dfrac{K-step+1}{i}\geq \dfrac{a}{b}\),即\(i\leq [\dfrac{b(K-step+1)}{a}]\),如果算出来的\(i\)大于int的最大值,那就以int的最大值为界,否则算一段时间就会爆掉的,体现为变成负数然后TLE。注意\(a′,b′\)进入下层时要约分,否则爆掉的几率会大大增加。
8 24点游戏 LGP1236
2020011600035
题意描述
几十年前全世界就流行一种数字扑克游戏,至今仍有人乐此不疲.在中国我们把这种游戏称为“算24点”。您作为游戏者将得到4个1-13(在扑克牌里用A代替1,J代替11,Q代替12,K代替13)之间的自然数作为操作数,而您的任务是对这4个操作数进行适当的算术运算,判断运算结果是否等于24。能输出1,不能输出0。
输入
四个牌面值。牌面值与牌面值之间用一个空格隔开。
输出
输出0或1。
题解
类似于全排列,只是需要对于当前数有四种运算。
9 虫食算[NOI2004] LGP1092
2020011600036
题意描述
所谓虫食算,就是原先的算式中有一部分被虫子啃掉了,需要我们根据剩下的数字来判定被啃掉的字母。来看一个简单的例子:
43#9865#045
+ 8468#6633
= 44445506678
其中#号代表被虫子啃掉的数字。根据算式,我们很容易判断:第一行的两个数字分别是5和3,第二行的数字是5。
现在,我们对问题做两个限制:
首先,我们只考虑加法的虫食算。这里的加法是N进制加法,算式中三个数都有N位,允许有前导的0。
其次,虫子把所有的数都啃光了,我们只知道哪些数字是相同的,我们将相同的数字用相同的字母表示,不同的数字用不同的字母表示。如果这个算式是N进制的,我们就取英文字母表午的前N个大写字母来表示这个算式中的0到N-1这N个不同的数字:但是这N个字母并不一定顺序地代表0到N-1)。输入数据保证N个字母分别至少出现一次。
BADC
+ CBDA
= DCCC
上面的算式是一个4进制的算式。很显然,我们只要让ABCD分别代表0123,便可以让这个式子成立了。你的任务是,对于给定的N进制加法算式,求出N个不同的字母分别代表的数字,使得该加法算式成立。输入数据保证有且仅有一组解.
输入
输入包含4行。第一行有一个正整数\(N\)(\(N\leq 26\)),后面的3行每行有一个由大写字母组成的字符串,分别代表两个加数以及和。这3个字符串左右两端都没有空格,从高位到低位,并且恰好有N位。
输出
输出包含一行。在这一行中,应当包含唯一的那组解。解是这样表示的:输出N个数字,分别表示A,B,C……所代表的数字,相邻的两个数字用一个空格隔开,不能有多余的空格。
样例输入
5
ABCED
BDACE
EBBAA
样例输出
1 0 3 4 2
题解
其实我们就是想知道ABCDE这几个字母对应01234的全排列,存在一个全排列满足竖式运算就行,这样算法就是简单了,为了加快速度,我们模拟竖式计算字母出现的顺序去搜索对应的数字。样例中字母从前往后出现的顺序是DEACB,对应的同一列的字母都确定了要检查是否矛盾,需要注意的是第一位是不能进位的。
10 反质数 [ZJOI2006]
2020011600037
题意描述
对于任何正整数\(x\),其约数的个数记作\(g(x)\)。例如\(g(1)=1\)、\(g(6)=4\)。
如果某个正整数\(x\)满足:\(g(x)>g(i)\), \(0<i<x\),则称\(x\)为反质数。例如,整数\(1,2,4,6\)等都是反质数。
现在给定一个数\(N\),你能求出不超过\(N\)的最大的反质数么?
输入
输入只有一行,一个数\(N\)(\(1\leq N\leq 2,000,000,000\))。
输出
输出也只有一行,为不超过\(N\)的最大的反质数。
题解
对于一个数\(n\)如果\(n={p_1}^{q_1}\times {p_2}^{q_2}\times ……\times {p_k}^{q_k}\)
其中\(p_i(0<i<=k)\)为质数
则它的约数个数\(=(q_1+1)\times(q_2+1)\times(q_3+1)\times……\times(q_k+1)\)
我们又发现要让这个数尽量小则需要同样的情况下
小质数的指数大……
即\(q_1\geq q_2\geq q_3\geq q_4\geq ……\geq q_k\)
然后爆搜解决……
由于是这样的,\(2\times 3\times 5\times 7\times 11\times 13\times 17\times 23\times 29\times 31>2\times 10^9\),所以最多用到这些质数。
好了一共9-10个质数,爆搜就可以了
11 [hdu2717] Catch That Cow
2020011600038
题意描述
已知\(x\)和\(y\),\(x\)只能通过\(x+1\),\(x-1\),\(2\times x\),问\(x\)到达\(y\)至少需要多少步?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号