[图]图的两种存储方式-邻接矩阵和邻接表
问题引入:
最近一直在研究图数据库的应用,后续也会关于图数据库写一个详细的介绍,记录下自己的学习收获,顺便也给后来人一个参考。
当你会用图数据库的时候,就一直在考虑,我的这么多数据(定点、边、属性之类)到底是咋存储的呢?就比如我问你关系型数据库mysql里数据咋存储的,大家都知道索引的话就是B+树结构,在检索方面肯定是可以做到效率更优(后续要是不太懒的话,也会在博客园记录下mysql索引和引擎结构),但是说到图数据库的时候,很少人就知道了,所以现在这里做个简单的科普,为什么说简单?相信你只看下面的几张图就能看懂。
当然作为科普,我可能还得多码点字介绍详细些。
邻接矩阵(无向图)
考虑到图是由顶点和边或弧两部分组成,合在一起比较困难,那就很自然地考虑到分为两个结构来分别存储。
顶点因为不区分大小、主次,所以用一个一维数组来存储是狠不错的选择。
而边或弧由于是顶点与顶点之间的关系,一维数组肯定就搞不定了,那我们不妨考虑用一个二维数组来存储。
于是我们的邻接矩阵方案就诞生了!
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
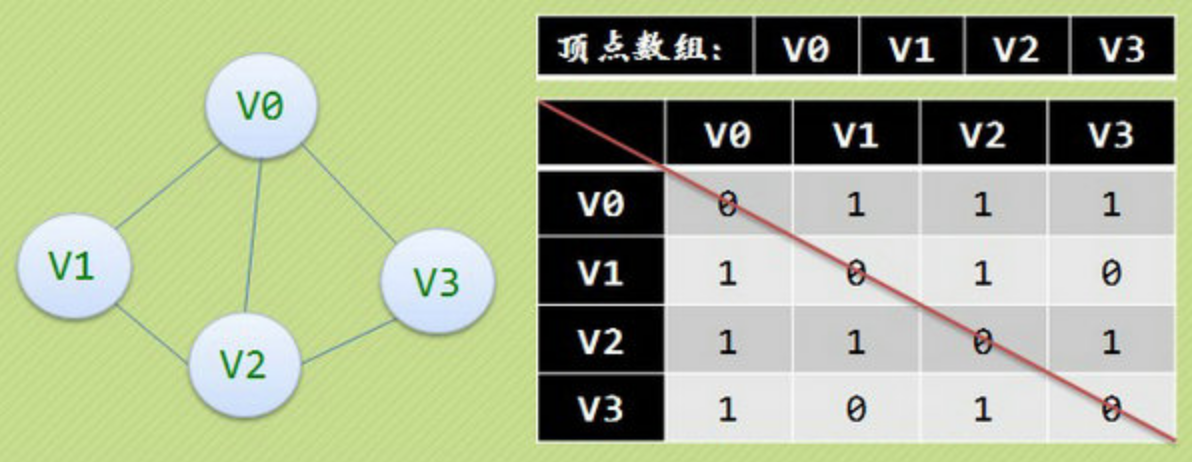
我们可以设置两个数组,顶点数组为vertex[4]={V0,V1,V2,V3},边数组arc[4][4]为对称矩阵(0表示不存在顶点间的边,1表示顶点间存在边)。
对称矩阵:所谓对称矩阵就是n阶矩阵的元满足a[i][j]=a[j][i](0<=i,j<=n)。即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的。
有了这个二维数组组成的对称矩阵,我们就可以很容易地知道图中的信息:
- 要判定任意两顶点是否有边无边就非常容易了;
- 要知道某个顶点的度,其实就是这个顶点Vi在邻接矩阵中第i行(或第i列)的元素之和;
- 求顶点Vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[i][j]为1就是邻接点咯。
邻接矩阵(有向图)
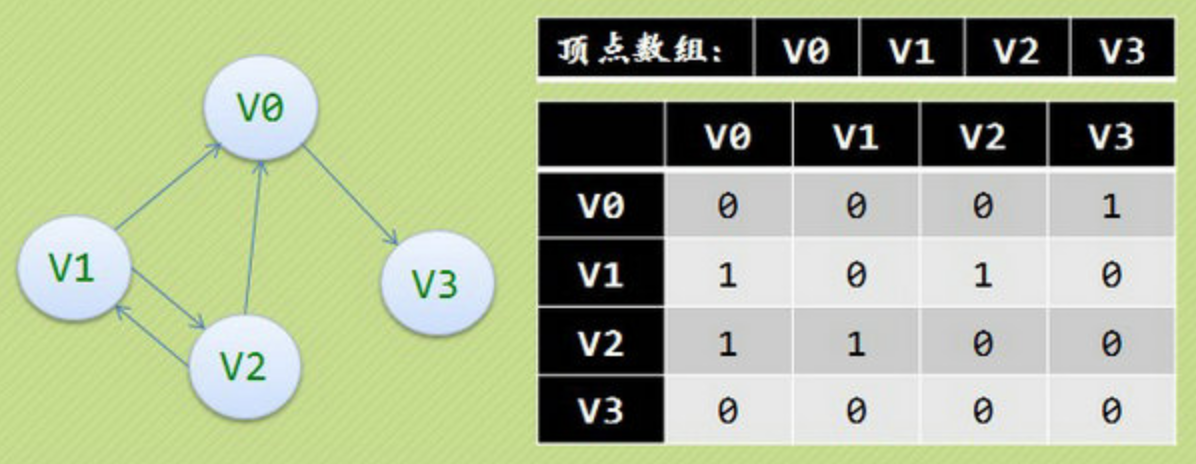
可见顶点数组vertex[4]={V0,V1,V2,V3},弧数组arc[4][4]也是一个矩阵,但因为是有向图,所以这个矩阵并不对称,例如由V1到V0有弧,得到arc[1][0]=1,而V0到V1没有弧,因此arc[0][1]=0。
另外有向图是有讲究的,要考虑入度和出度,顶点V1的入度为1,正好是第V1列的各数之和,顶点V1的出度为2,正好是第V1行的各数之和。
邻接矩阵(网)
在图的术语中,我们提到了网这个概念,事实上也就是每条边上带有权的图就叫网。
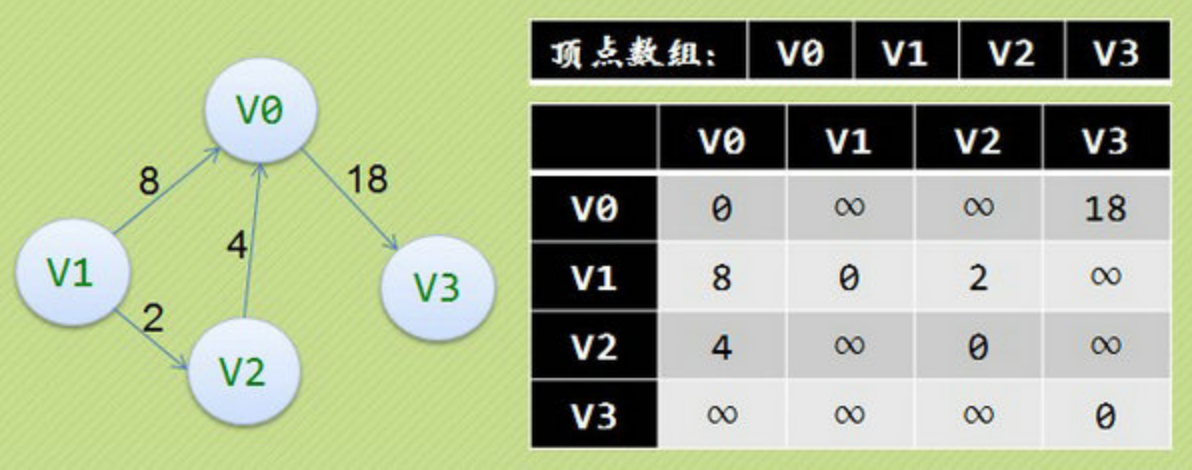
邻接表
上面是邻接矩阵的概念,比较好了解,那为什么要引入邻接表呢?
考虑下:对于边数相对顶点较少的图,这种结构是存在对存储空间的极大浪费的。因此我们考虑另外一种存储结构方式:邻接表(Adjacency List),即数组与链表相结合的存储方法。
邻接表的处理方法是这样的。
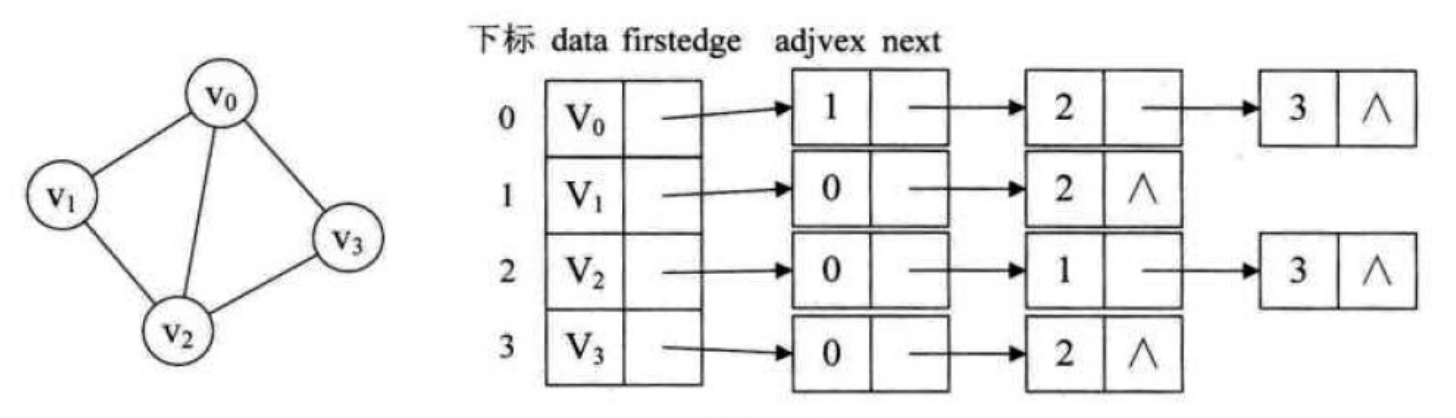
1、图中顶点用一个一维数组存储,另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
2、图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点vi的边表,有向图称为顶点vi作为弧尾的出边表。
下图是一个无向图的邻接表结构:
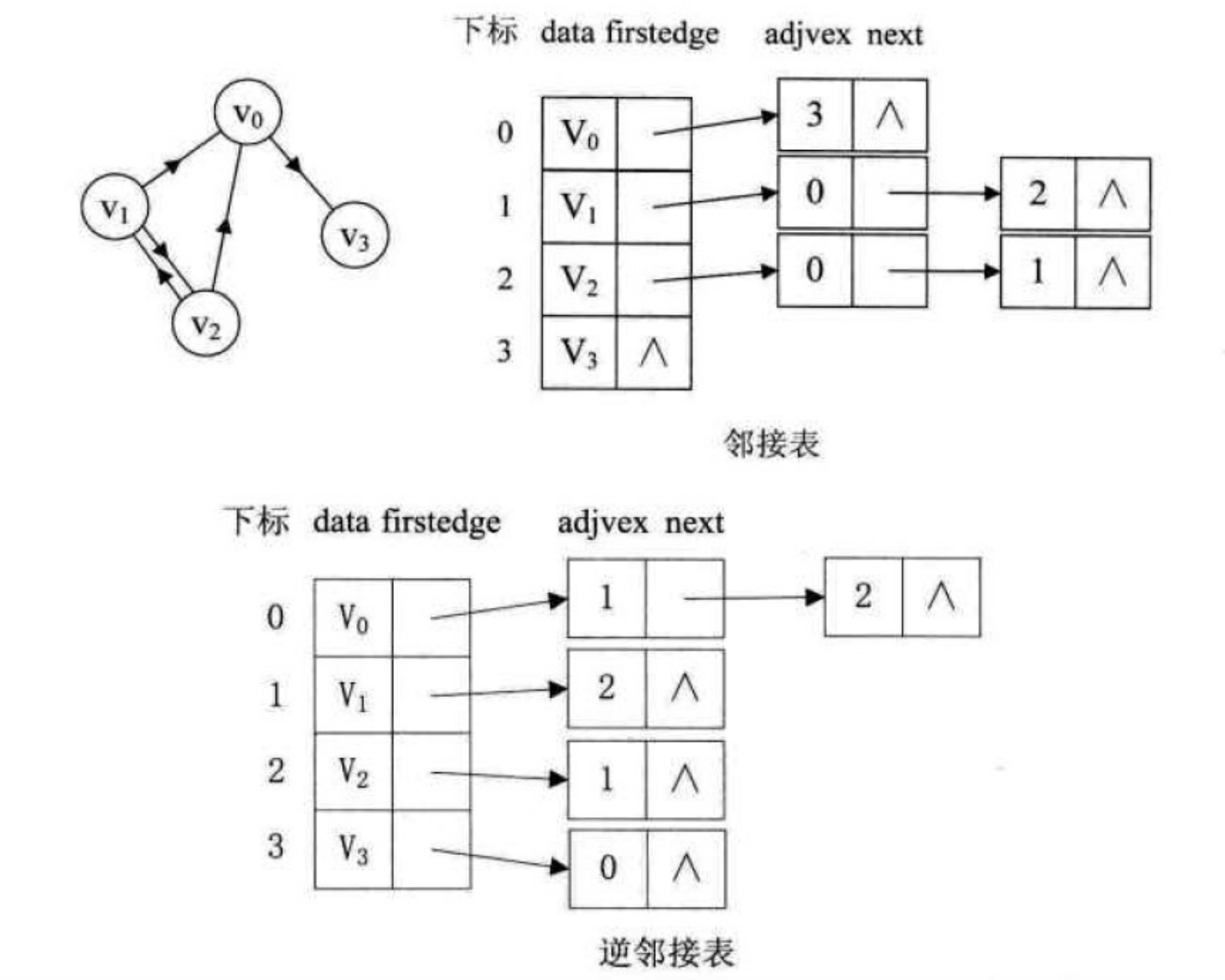
若是有向图,邻接表的结构是类似的,如下图,以顶点作为弧尾来存储边表容易得到每个顶点的出度,而以顶点为弧头的表容易得到顶点的入度,即逆邻接表。
下图是一个有向图的邻接表结构:
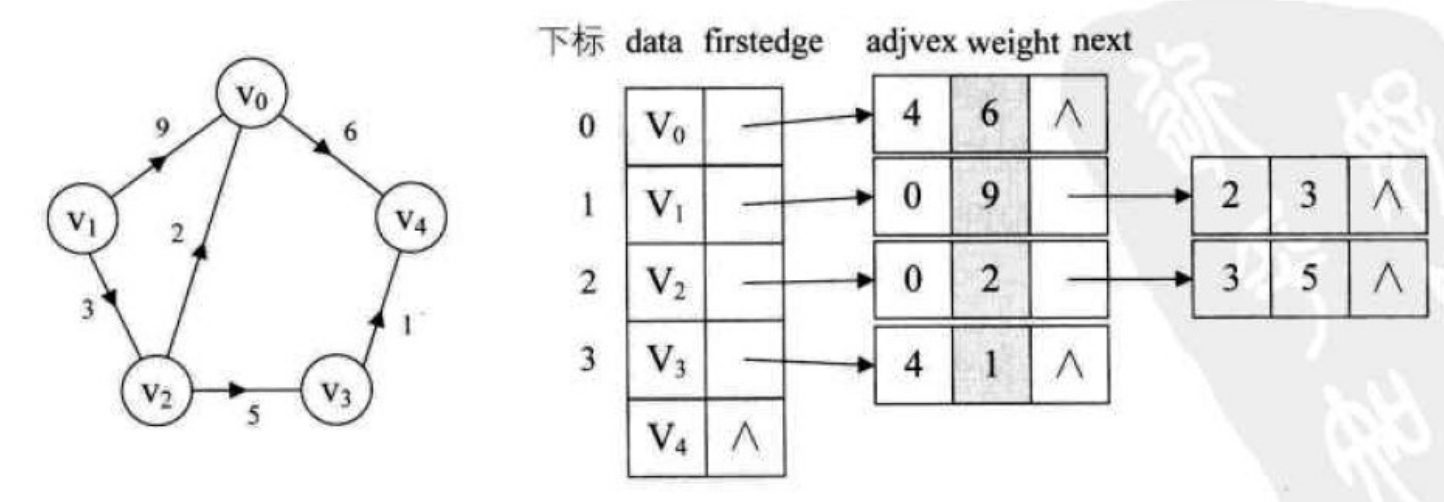
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可,如下图所示:
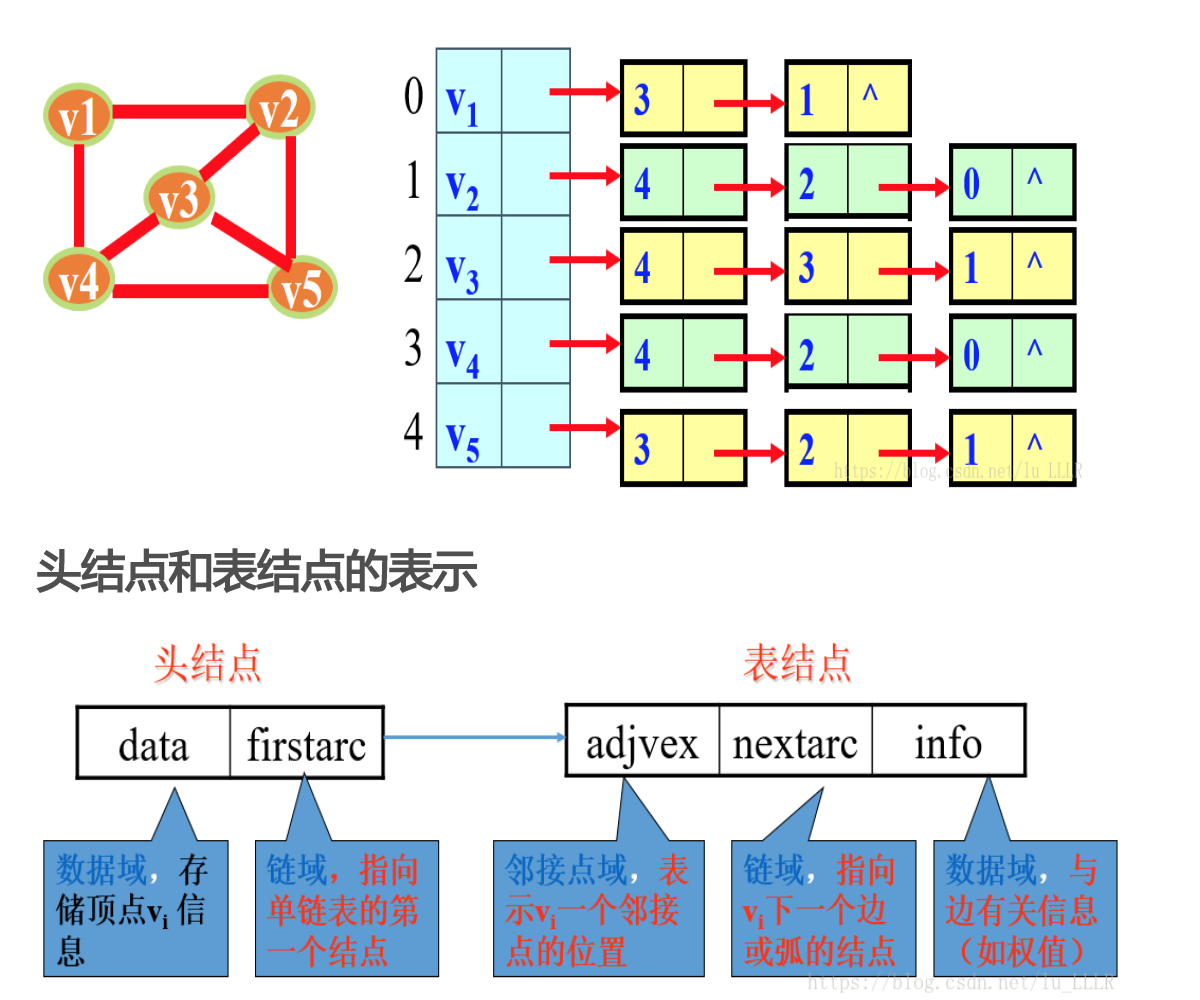
有了这样的数据结构,我们就大概可以知道为什么图数据库在一些关系型的挖掘上有很大的优势了,接下来还要介绍下图的遍历方式:深度优先遍历和广度优先遍历,这样图的工作原理就清晰啦。
主要内容转自:
https://www.cnblogs.com/jiaqingshareing/p/6008768.html
https://blog.csdn.net/jnu_simba/article/details/8866844



 浙公网安备 33010602011771号
浙公网安备 33010602011771号