正则化详解
一、为什么要正则化
学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过拟合(over-fitting)的问题,可能会导致它们效果很差。正则化(regularization)技术,可以改善或者减少过度拟合问题,进而增强泛化能力。泛化误差(generalization error)= 测试误差(test error),其实就是使用训练数据训练的模型在测试集上的表现(或说性能 performance)好不好。
如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为0),但是可能会不能推广到新的数据。
下图是一个回归问题的例子:
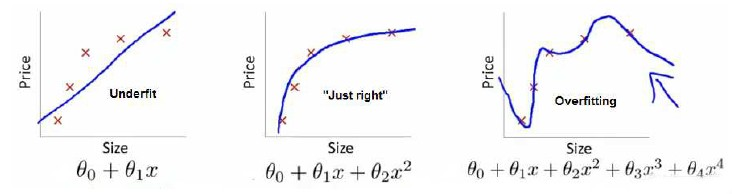
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
分类问题中也存在这样的问题:
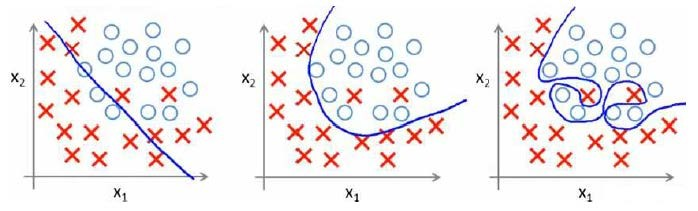
就以多项式理解,$x$的次数越高,拟合的越好,但相应的预测的能力就可能变差。
如果我们发现了过拟合问题,可以进行以下处理:
1、丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)。
2、正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
二、正则化的定义
正则化的英文 Regularizaiton-Regular-Regularize,直译应该是"规则化",本质其实很简单,就是给模型加一些规则限制,约束要优化参数,目的是防止过拟合。其中最常见的规则限制就是添加先验约束,常用的有L1范数和L2范数,其中L1相当于添加Laplace先验,L相当于添加Gaussian先验。
三、L1正则和L2正则
在介绍L1范数、L2范数之前,我们先介绍以下LP范数。
3.1 范数
范数简单可以理解为用来表征向量空间中的距离,而距离的定义很抽象,只要满足非负、自反、三角不等式就可以称之为距离。
LP范数不是一个范数,而是一组范数,其定义如下:
$\left \| x \right \|_{p}=(\sum_{i}^{n}x_{i}^{p})^{\frac{1}{p}}$
$\left \| x \right \|_{p}=(\sum_{i}^{n}x_{i}^{p})^{\frac{1}{p}}$
$p$的范围是[1,∞)[1,∞)。$p$在(0,1)(0,1)范围内定义的并不是范数,因为违反了三角不等式。
根据$p$的变化,范数也有着不同的变化,借用一个经典的有关P范数的变化图如下:

上图表示了$p$从0到正无穷变化时,单位球(unit ball)的变化情况。在P范数下定义的单位球都是凸集,但是当0<𝑝<10<p<1时,在该定义下的unit ball并不是凸集(这个我们之前提到,当0<𝑝<10<p<1时并不是范数)。
- L1范数
当p=1时,是L1范数,其表示某个向量中所有元素绝对值的和。
- L2范数
当p=2时,是L2范数, 表示某个向量中所有元素平方和再开根, 也就是欧几里得距离公式。
3.2 L2 正则化直观解释
L2正则化公式非常简单,直接在原来的损失函数基础上加上权重参数的平方和:
其中,$E_{in}$是未包含正则化项的训练样本误差,$\lambda$是正则化参数,可调。但是正则化项是如何推导的?接下来,我将详细介绍其中的物理意义。
我们知道,正则化的目的是限制参数过多或者过大,避免模型更加复杂。例如,使用多项式模型,如果使用 10 阶多项式,模型可能过于复杂,容易发生过拟合。所以,为了防止过拟合,我们可以将其高阶部分的权重$w$限制为 0,这样,就相当于从高阶的形式转换为低阶。
为了达到这一目的,最直观的方法就是限制$w$的个数,但是这类条件属于 NP-hard 问题,求解非常困难。所以,一般的做法是寻找更宽松的限定条件:
$\sum_{j}^{}w_{j}^{2}\leq C$
上式是对$w$的平方和做数值上界限定,即所有$w$的平方和不超过参数$C$。这时候,我们的目标就转换为:最小化训练样本误差$E_{in}$,但是要遵循$w$平方和小于$C$的条件。
下面,我用一张图来说明如何在限定条件下,对$E_{in}$进行最小化的优化。
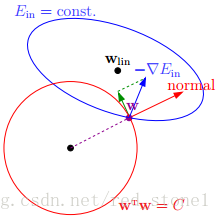
如上图所示,蓝色椭圆区域是最小化$E_{in}$区域,红色圆圈是$w$的限定条件区域。在没有限定条件的情况下,一般使用梯度下降算法,在蓝色椭圆区域内会一直沿着$w$梯度的反方向前进,直到找到全局最优值 wlin。例如空间中有一点$w$(图中紫色点),此时$w$会沿着 -∇Ein 的方向移动,如图中蓝色箭头所示。但是,由于存在限定条件,$w$不能离开红色圆形区域,最多只能位于圆上边缘位置,沿着切线方向。$w$的方向如图中红色箭头所示。
那么问题来了,存在限定条件,$w$最终会在什么位置取得最优解呢?也就是说在满足限定条件的基础上,尽量让$E_{in}$最小。
我们来看,$w$是沿着圆的切线方向运动,如上图绿色箭头所示。运动方向与$w$的方向(红色箭头方向)垂直。运动过程中,根据向量知识,只要 -∇Ein 与运行方向有夹角,不垂直,则表明$-\triangledown E_{in}$仍会在$w$切线方向上产生分量,那么$w$就会继续运动,寻找下一步最优解。只有当$-\triangledown E_{in}$与$w$的切线方向垂直时,$-\triangledown E_{in}$在$w$的切线方向才没有分量,这时候$w$才会停止更新,到达最接近$wlin$的位置,且同时满足限定条件。

$-\triangledown E_{in}$与$w$的切线方向垂直,即$-\triangledown E_{in}$与$w$的方向平行。如上图所示,蓝色箭头和红色箭头互相平行。这样,根据平行关系得到:
$-\triangledown E_{in}+\lambda w=0$
移项,得:
$\triangledown E_{in}+\lambda w=0$
这样,我们就把优化目标和限定条件整合在一个式子中了。也就是说只要在优化$E_{in}$的过程中满足上式,就能实现正则化目标。
接下来,重点来了!根据最优化算法的思想:梯度为 0 的时候,函数取得最优值。已知$-\triangledown E_{in}$是$E_{in}$的梯度,观察上式,λw 是否也能看成是某个表达式的梯度呢?
当然可以!$\lambda w$可以看成是$\frac{1}{2}\lambda^{2} w$的梯度:
$\frac{\partial }{\partial w}(\frac{1}{2}\lambda w^{2})=\lambda w$
这样,我们根据平行关系求得的公式,构造一个新的损失函数:
$E_{aug}=E_{in}+\frac{\lambda }{2}w^{2}$
之所以这样定义,是因为对$E_{aug}$求导,正好得到上面所求的平行关系式。上式中等式右边第二项就是L2正则化项。
这样, 我们从图像化的角度,分析了L2正则化的物理意义,解释了带L2正则化项的损失函数是如何推导而来的。
3.3 L1 正则化直观解释
L1正则化公式也很简单,直接在原来的损失函数基础上加上权重参数的绝对值:
$L=E_{in}+\lambda \sum_{j}^{}\left |w_{j} \right |$
仍然用一张图来说明如何在L1正则化下,对$E_{in}$进行最小化的优化。
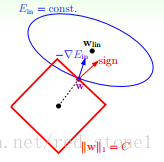
$E_{in}$优化算法不变,L1正则化限定了$w$的有效区域是一个正方形,且满足 |w| < C。空间中的点$w$沿着$-\triangledown E_{in}$的方向移动。但是,$w$不能离开红色正方形区域,最多只能位于正方形边缘位置。其推导过程与L2类似,此处不再赘述。
3.4 L1、L2正则的区别
引入PRML一个经典的图来说明L1和L2的区别,如下图所示:
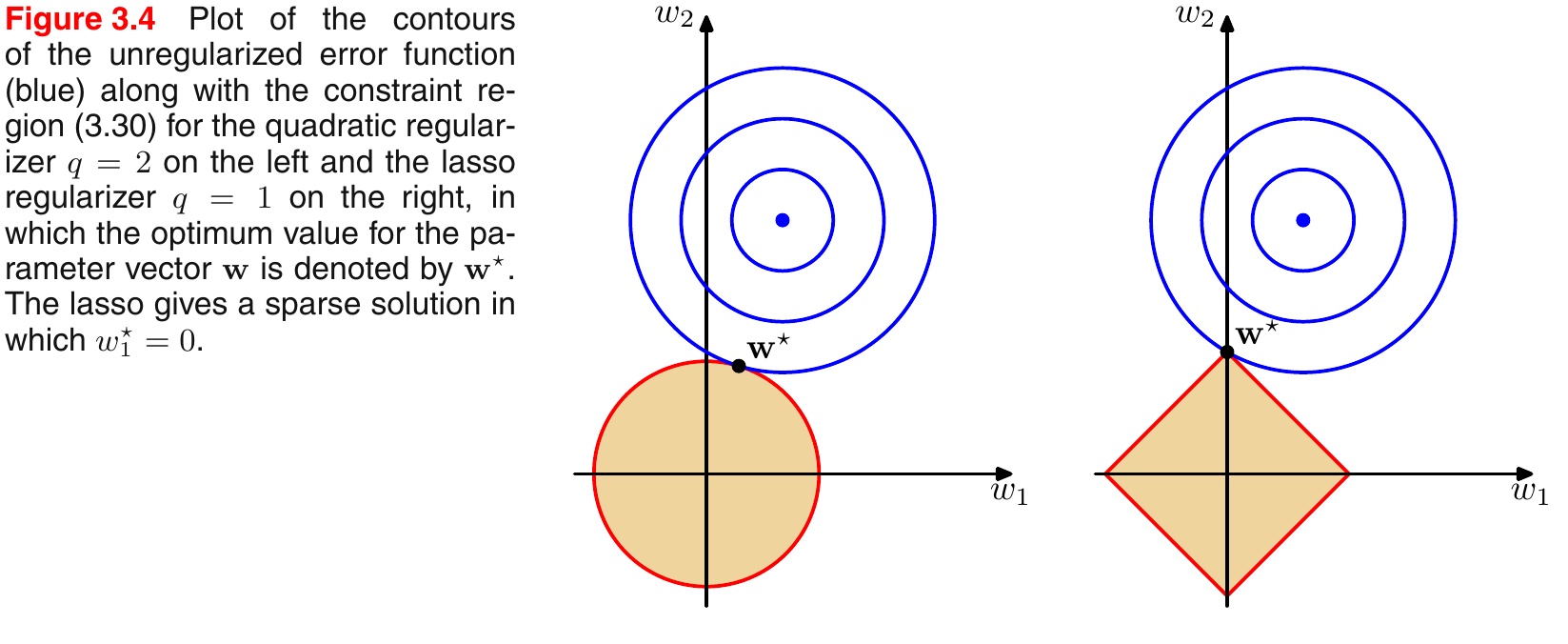
- L1范数相当于加入了一个Laplacean先验;
- L2范数相当于加入了一个Gaussian先验。
如下图所示:

总结
1、添加正则化相当于参数的解空间添加了约束,限制了模型的复杂度;正则化参数 λ越大,约束越严格,太大容易产生欠拟合。正则化参数 λ越小,约束宽松,太小起不到约束作用,容易产生过拟合。
2、L1正则化的形式是添加参数的绝对值之和作为结构风险项,L2正则化的形式添加参数的平方和作为结构风险项。
3、稀疏性:L1正则化鼓励产生稀疏的权重,即使得一部分权重为0,用于特征选择;L2鼓励产生小而分散的权重,鼓励让模型做决策的时候考虑更多的特征,而不是仅仅依赖强依赖某几个特征,可以增强模型的泛化能力,防止过拟合。 稀疏的解除了计算量上的好处之外,更重要的是更具有“可解释性”。如果不是为了进行特征选择,一般使用L2正则化模型效果更好。
4、计算效率:L1-正则没有一个解析解(analytical solution),但是L2正则有,这使得L2正则可以被高效的计算。可是,L1正则的解有稀疏的属性,它可以和稀疏算法一起用,这可以是计算更加高效。
5、鲁棒性:概括起来就是L1对异常点不太敏感,而L2则会对异常点存在放大效果。最小绝对值偏差的方法应用领域很广(L1-norm),相比最小均方的方法,它的鲁棒性更好,LAD能对数据中的异常点有很好的抗干扰能力,异常点可以安全的和高效的忽略,这对研究帮助很大。如果异常值对研究很重要,最小均方误差则是更好的选择。对于L2-norm,由于是均方误差,如果误差>1的话,那么平方后,相比L-norm而言,误差就会被放大很多。因此模型会对样例更敏感。如果样例是一个异常值,模型会调整最小化异常值的情况,以牺牲其它更一般样例为代价,因为相比单个异常样例,那些一般的样例会得到更小的损失误差。
6、计算效率:L1-norm没有一个解析解(analytical solution),但是L2-nom有,这使得L2-norm可以被高效的计算。可是,L1-norm的解有稀疏的属性,它可以和稀疏算法一起用,这可以是计算更加高效。
四、其它正则化方法
除了加一个惩罚项,其实正则化还有多种多样的方法,但是总体的思想史一样的,就是想办法使得我们的模型不要那么复杂。下面简单介绍两种方法:
4.1 Dropout
Dropout是深度学习中经常采用的一种正则化方法。它的做法可以简单的理解为在DNNs训练的过程中以概率𝑝p丢弃部分神经元,即使得被丢弃的神经元输出为0。Dropout可以实例化的表示为下图:
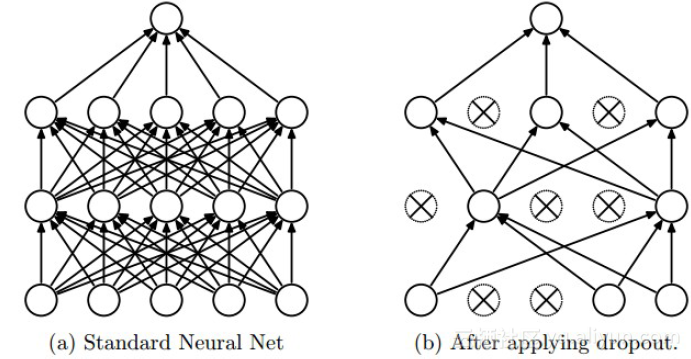
我们可以从两个方面去直观地理解Dropout的正则化效果:
- 在Dropout每一轮训练过程中随机丢失神经元的操作相当于多个DNNs进行取平均,因此用于预测时具有vote的效果。
- 减少神经元之间复杂的共适应性。当隐藏层神经元被随机删除之后,使得全连接网络具有了一定的稀疏化,从而有效地减轻了不同特征的协同效应。也就是说,有些特征可能会依赖于固定关系的隐含节点的共同作用,而通过Dropout的话,就有效地组织了某些特征在其他特征存在下才有效果的情况,增加了神经网络的鲁棒性。
4.2 Batch Normalization
批规范化(Batch Normalization)严格意义上讲属于归一化手段,主要用于加速网络的收敛,但也具有一定程度的正则化效果。
这里借鉴下魏秀参博士的知乎回答中对covariate shift的解释(这里)。
注以下内容引自魏秀参博士的知乎回答:
大家都知道在统计机器学习中的一个经典假设是“源空间(source domain)和目标空间(target domain)的数据分布(distribution)是一致的”。如果不一致,那么就出现了新的机器学习问题,如transfer learning/domain adaptation等。而covariate shift就是分布不一致假设之下的一个分支问题,它是指源空间和目标空间的条件概率是一致的,但是其边缘概率不同。大家细想便会发现,的确,对于神经网络的各层输出,由于它们经过了层内操作作用,其分布显然与各层对应的输入信号分布不同,而且差异会随着网络深度增大而增大,可是它们所能“指示”的样本标记(label)仍然是不变的,这便符合了covariate shift的定义。
BN的基本思想其实相当直观,因为神经网络在做非线性变换前的激活输入值随着网络深度加深,其分布逐渐发生偏移或者变动(即上述的covariate shift)。之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近,所以这导致后向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,避免因为激活函数导致的梯度弥散问题。所以与其说BN的作用是缓解covariate shift,倒不如说BN可缓解梯度弥散问题。
4.3 early-stopping
这个很简单,说白了就是不要训练那么久了,见好就收。这里不赘述,详见另外一篇博客《深度学习中过拟合、欠拟合问题及解决方案》。
参考:
https://www.cnblogs.com/weststar/p/11662760.html
https://www.cnblogs.com/maybe2030/p/9231231.html#_label3



 浙公网安备 33010602011771号
浙公网安备 33010602011771号