贪心算法
贪心算法
一、什么叫贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
二、贪心算法使用范围
1、原问题复杂度过高;
2、求全局最优解的数学模型难以建立;
3、求全局最优解的计算量过大;
4、没有太大必要一定要求出全局最优解,“比较优”就可以。
三、贪心选择性质
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心算法求解的关键特征。
四、贪心算法的实现框架
从问题的某一初始解出发:while (朝给定总目标前进一步)
{
利用可行的决策,求出可行解的一个解元素。
}
由所有解元素组合成问题的一个可行解;
五、举例分析
1、背包问题:

假如我们有一个可以装100kg物品的背包,我们有5种豆子,每种豆子的总量和总价值各不相同。为了让背包中所装的物品的总价值最大,我们如何选择装哪些豆子,每种装多少?
| 物品 | 总量(克) | 总价值(元) | 单价(元/克) |
| 黄豆 | 100 | 100 | 1 |
| 绿豆 | 30 | 90 | 3 |
| 黑豆 | 60 | 120 | 2 |
| 青豆 | 20 | 80 | 4 |
| 红豆 | 50 | 75 | 1.5 |
分析:
直观来想,我们的总重是100kg是限制的,要求装的物品总价值最大,那么我们可以把各种豆子的单价计算下每种豆子的单价,然后按照从高到低排序,每次装完最有价值的豆子后,再继续装稍次价值的豆子,直到装满整个背包。
这就跟我们平时去吃自助餐一样,我们的胃口基本能吃多少是固定的,如果我们想要挣回本的话就要去吃那些单价很贵的食物,比如海鲜之类的,而且会尽量不去吃米饭这种单价很便宜的食物,这其实就是我们平时生活中贪心算法的例子。
分糖果:
我们有m个糖果和n个孩子,现在要把糖果分给这些孩子吃,但是糖果少m<n,所以只有一部分孩子能够得到糖果,每个糖果的大小不一样,m个糖果大小分别为s1,s2,s3….sm.除此之外,每个孩子对糖果大小需求不一样,假设这些孩子对糖果的需求大小分别为g1,g2…gn,只有糖果大小大于孩子对糖果需求的时候,他们才会满足,求我们如何分糖果才能够满足最多数量的孩子。
分析:
这个问题是我们选择一部分小孩分给他们糖果,要满足一共最多只能分给m个孩子,还要让满意的孩子最多。和上一个问题类似,就是我们按照孩子对糖果满足从小到大排序,然后依次选能够满足孩子需求的最小糖果,这样依次分下去就可以达到满足最多孩子的目的。
这类题目的特点:
1) 都是有限制的请求下求解
背包问题限制是100kg,分糖果问题限制问题是最多有m个糖果。
2)都是求限制条件下的最优解,背包问题是求最大价值,分糖果是为了求满足最多孩子。
3)每步都是局部最优的,比如背包问题的时候,因为要求最大价值,所以先装最贵的,这样质量不变的情况下,增加的价值最大;分糖果也一样,是在最小糖果的情况下满足一个孩子,满足孩子的都是一个,那么我们需要减少分出去的糖果。
2、区域完全覆盖问题
数轴上有n个闭区间[a,b],选择尽量少的区间覆盖一条制定的线段该区间。
如:
在[1,8]的数轴上有区间[2,6],[1,4],[3,6],[3,7],[6,8],[2,4],[3,5],找出最少的线段来覆盖[2,8]这个区间。
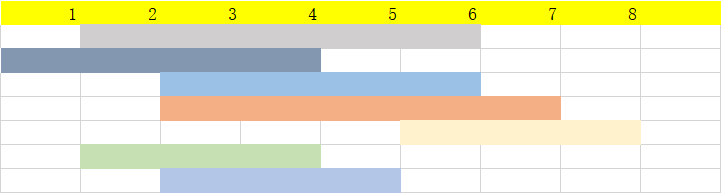
分析:
①将每一个区间按照左端点递增顺序排列,拍完序后为[1,4],[2,4],[2,6],[3,5],[3,6],[3,7],[6,8]。
②设置一个变量表示已经覆盖到的区域。再剩下的线段中找出所有左端点小于等于当前已经覆盖到的区域的右端点的线段中,右端点最大的线段在加入,直到已经覆盖全部的区域
③过程:
假设第一步加入[1,4],那么下一步能够选择的有[2,6],[3,5],[3,6],[3,7],由于7最大,所以下一步选择[3,7],最后一步只能选择[6,8],这个时候刚好达到了8退出,所选区间为3
④贪心证明:
需要最少的线段进行覆盖,那么选取的线段必然要尽量长,而已经覆盖到的区域之前的地方已经无所谓了,(可以理解成所有的可以覆盖的左端点都是已经覆盖到的地方),那么真正能够使得线段更成的是右端点,左端点没有太大的意义,所以选择右端点来覆盖。
六、例题分析
(1)摘果子
题目描述:
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过 n-1 次合并之后, 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 11 ,并且已知果子的种类 数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有 3种果子,数目依次为 1 , 2 , 9 。可以先将 1 、 2 堆合并,新堆数目为 3 ,耗费体力为 3 。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12 ,耗费体力为 12 。所以多多总共耗费体力 3+12=15。可以证明 15 为最小的体力耗费值。
输入格式
共两行。
第一行是一个整数 n(1≤n≤10000) ,表示果子的种类数。
第二行包含 n个整数,用空格分隔,第 i个整数 ai(1≤ai≤20000) 是第 i种果子的数目。
输出格式
一个整数,也就是最小的体力耗费值。输入数据保证这个值小于 2^{31} 。
输入输出样例
输入 #1
3
1 2 9
输出 #1
15
说明/提示
对于30%的数据,保证有n≤1000:
对于50%的数据,保证有n≤5000;
对于全部的数据,保证有n≤10000。
思路:
代码:
#include<iostream> #include<algorithm> using namespace std; int main() { int n; cin >> n; int fruit[10000]; int strength = 0; for (int i = 0;i < n;++i) { cin >> fruit[i]; } sort(fruit, fruit + n);//把fruit进行升序排序 for (int i = 0;i < n - 1;++i) { fruit[i + 1] += fruit[i];//两堆合并 strength += fruit[i + 1];//记录花费的力气 int temp = fruit[i + 1]; int j = i + 2; for (;j < n;++j) { if (temp < fruit[j]) break; } for (int k = i + 1;k < j - 1;++k) { fruit[k] = fruit[k + 1]; } fruit[j - 1] = temp; } cout << strength; }
跳跃游戏——a
题目描述:
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断是否能够到达最后一个位置。
问题分析:
给定一个数组,数组中每个位置的数字代表当前位置i能够向前跳跃num[i]的距离,然后判断最后能够从第一个位置跳到最后一个位置。这道题的难点就在于每次跳多远的距离算合适呢?如果从i的位置能跳num[i]距离最远能到达j的位置,那么这中间的任何一个位置我们都能跳到,但我们具体是跳到i–j之间的哪个位置才是真正合适的位置?利用贪心的思想我们的目的是判断最后能否跳到最后一个位置,其实就是只要能保证在i–j之间跳到一个能够在下一次跳的更远的距离,那么这个位置就是最合适的位置。
实例1:
输入: [2,3,1,1,4]
输出: true
解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。
实例2:
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
算法思想:
1、首先根据num[]数组求出index[i]=i+num[i];
2、设置一个变量jump表示当前的位置,设置一个变量max_index表示当前指针经过的index[]数组中所能达到的最远距离
3、jump变量逐步往后循环,当到达index[]最后的时候或者是变量max_index的值小于jump的值的时候停止循环,jump能走到数组的最后表示能够到达最后,如果是因为变量max_index的值小于jump的值造成的循环终止,那么就表示不能达到最后。
#include<iostream> #include<vector> #include<algorithm> #include<cstring> #include<string> using namespace std; bool function(vector<int>& num) { vector<int>index;//索引值 for (int i = 0;i < num.size();++i) { index.push_back(i + num[i]); } int jump = 0; int max_index = index[0];//目前最大能走的位置 while (jump < index.size() && jump <= max_index) { if (max_index < index[jump]) { max_index = index[jump]; } jump++; if (max_index >= num.size()) { return true; } } return false; } int main() { vector<int> v; v.push_back(2); v.push_back(3); v.push_back(1); v.push_back(1); v.push_back(4); cout << function(v); }
贪心算法-移除K个数字
题目描述
给定一个以字符串表示的非负整数 num,移除这个数中的 k 位数字,使得剩下的数字最小。
注意:
num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。
题目分析:
题目简介明了,就是把给定的数字删除指定个数的数字使删除之后的数字是同等位数数字中最小的那个。但是需要注意的是,题目中给的数字是字符串的形式并且输出结果也是字符串的形式,这就涉及到字符串和数字之间的相互转化问题。
题目中要求删除的数字个数是不确定的,那么我们可以根据数学知识先分析当我们删除一个数字的时候应该怎样删除才能保证删除之后的数字是最小的呢?依据下边的数字1432219为例,当我们要删除一个数字的时候,我们需要在左边(高位)尽可能的删除较大的数字。最后发现删除4之后是最小的数字,其实仔细分析就会发现:删除这一个数字就是从左边的高位1开始比较,当发现后一个数字比前一个数字小的时候我们就需要把前一个数字删除掉,这样就能保证满足要求
输入: num = “1432219”, k = 3
输出: “1219”
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
算法思想:
1、首先把当前给定的字符串表示的数字从高位开始逐个分离出来
2、设置一个栈,用于存放字符串分离出来的数字,从高到底逐个压入栈中。但是这里涉及到两个问题:栈是否为空、压入栈的数字是否是0
3、每分离出来一个数字,就进行一些判断:当前待入栈的数字和栈顶元素比较,如果栈顶元素大且K的值要大于0(保证移除指定个数的数字)且栈不为空就要先执行出栈操作然后再把这个待入栈元素入栈。
4、如果不满足3的情况,依然要考虑站是否为空的情况和待入栈的元素值是否为0的情况,因为当栈为空且待入栈的元素值为0的时候也不能入栈。除了这种情况之后其他情况都是可以入栈的。
5、如果是一个12345这样情况的数字,我们发现执行完3和4的情况之后K的值依然是大于0的。那么当上边的过程执行完毕我们还要单独判断K的值是否大于0,如果大于0的话,就要从栈顶删除若干个元素是k的值为0.
6、最后取出栈中元素组成字符串输出结果。
代码:
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
string function(string str, int k)
{
vector<int> v;
string result="";
int a = str[0] - '0';
v.push_back(a);//放入最高位数字
for (int i = 1;i < str.length();++i)
{
int num = str[i] - '0';//依次放入数字
while ( k > 0 && v[v.size()-1] > num)//满足要求的时候
{
v.pop_back();
k--;
}
if (num != 0 )//不能放入0
{
v.push_back(num);
}
}
while (v.size() != 0 && k > 0)//12345这种情况 k没有等于0 但是数字都放入栈中了
{
v.pop_back();
k--;
}
for(int i=0;i<v.size();++i)
{
result.append(1,v[i] + '0');
}
return result;
}
int main()
{
cout << function("1432219", 3);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号