正则化
过拟合问题
变量过多的时候容易出现,训练出来的假设能很好地拟合训练集,但是无法很好地泛化到新的样本中,导致无法准确预测
解决方法:
1.尽量减少选取特征变量的数量(模型选择算法:可以自动选择特征) ,同时也舍弃了一些特征
2.正则化(保留所有特征,减少量级或参数θ的大小)

加入惩罚增大两个参数带来的效果,相当于其值接近0,可以得到一个更简单的假设模型,而且不容易出现过拟合问题
对每个θ都添加惩罚项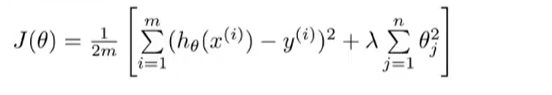
缩小参数可以达到下面蓝色曲线转变成洋红色(更平滑)
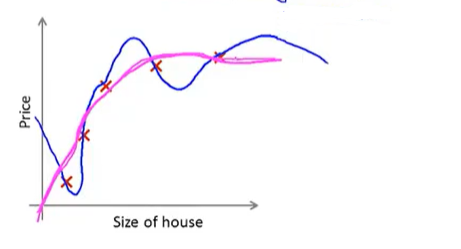
λ正则化参数:控制两个不同目标之间的取舍 1.更好的拟合训练集 2.保持参数尽量地小 。控制两者之间的平衡关系,更优拟合训练集的目标
若λ设置过大,θ值都接近于0,假设模型就几乎相当于一条直线,不太好(要选择合适的正则化参数λ)
多重选择,很多方法自动选择正则化参数λ
1.对正则化代价函数J(θ)用梯度下降法进行最小化

从直观看,只是每次更新θ值得时候,把θ乘以一个比1小一点点的数值,其中的数学原理黑盒
2.正则化作用到正规方程
之前的正规方程求J(θ)的全局最小值
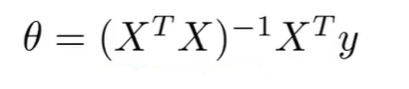
引进正则化后
X单独的训练样本 。 Y 标签值 , n 是特征数量,m是样本数量
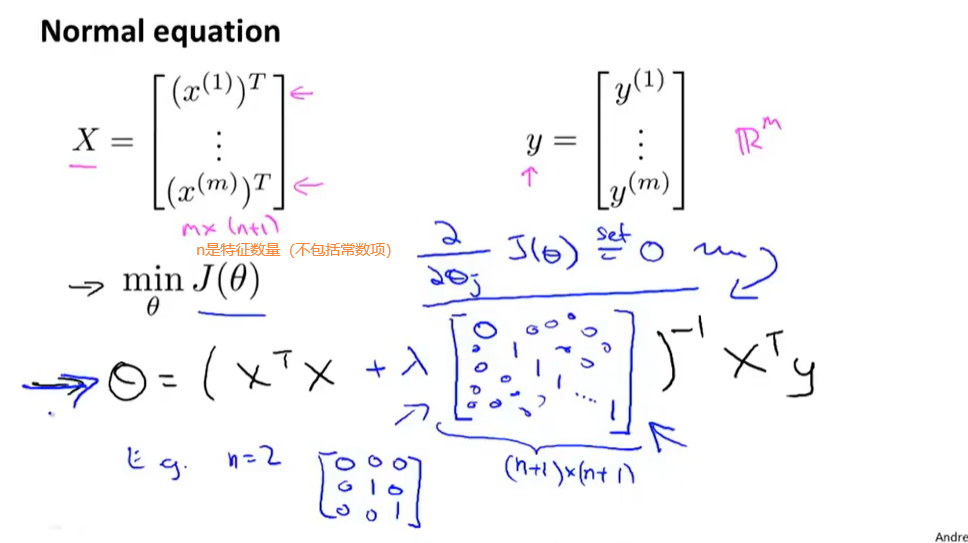
相关奇异矩阵问题

逻辑回归的正则化
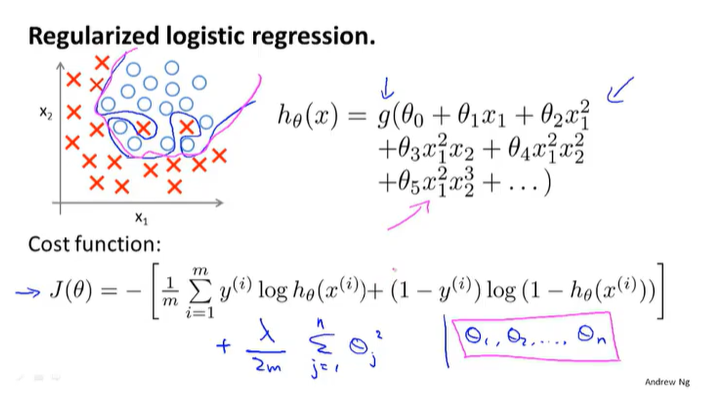
需要注意,逻辑回归与线性回归的梯度下降公式相似,但是其中的hθ意义是不同的
线性回归: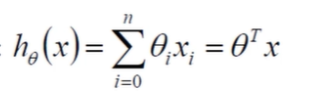
逻辑回归: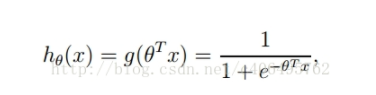




 浙公网安备 33010602011771号
浙公网安备 33010602011771号