C语言II博客作业02

这个作业属于哪个课程	https://edu.cnblogs.com/campus/zswxy/CST2020-2
这个作业要求在哪里	https://edu.cnblogs.com/campus/zswxy/CST2020-2/homework/11810
这个作业的目标	掌握更多解题方法，进行对数组知识的运用和练习
学号	20208990
**
2.1 完成PTA作业，并给出编程题完成截图（5分）**
第一题：

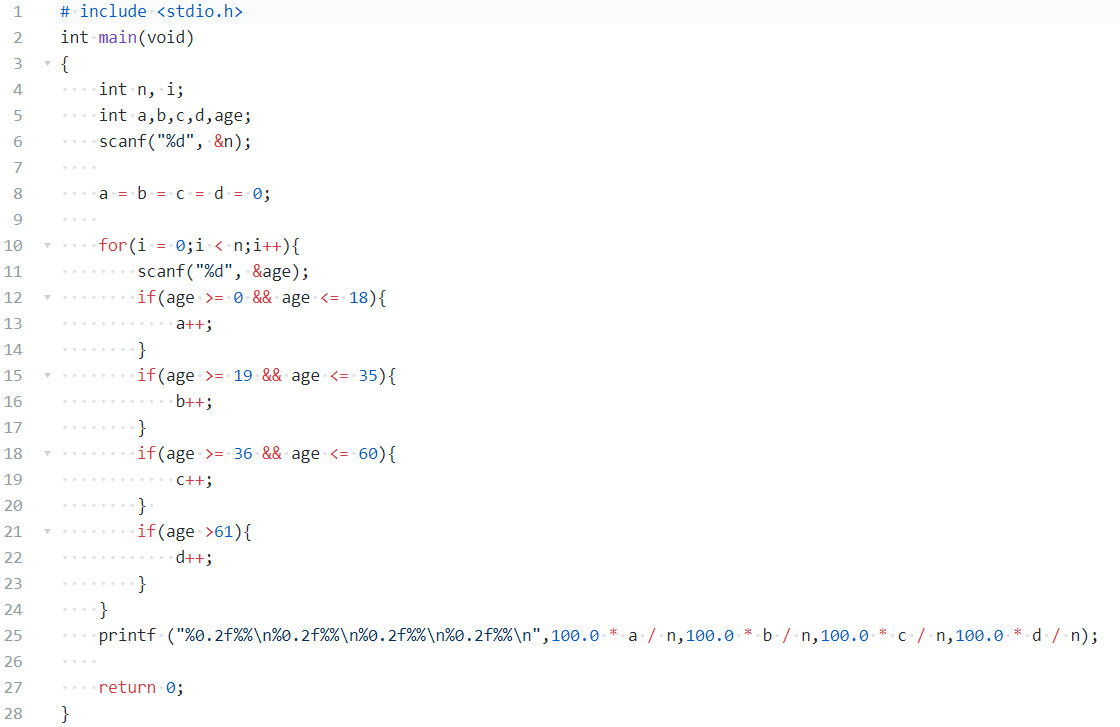第二题：

2.2 题目：快速寻找满足条件的两个数
能否快速找出一个数组中的两个数字，让这两个数字之和等于一个给定的值，为了简化起见，我们假设这个数组中肯定存在至少一组符合要求的解。

解法一：采用穷举法，从数组中任意取出两个数字，计算两者之和是否为给定的数字。

解法二：对数组中的每个数字arr[i]都判别Sum-arr[i]是否在数组中。

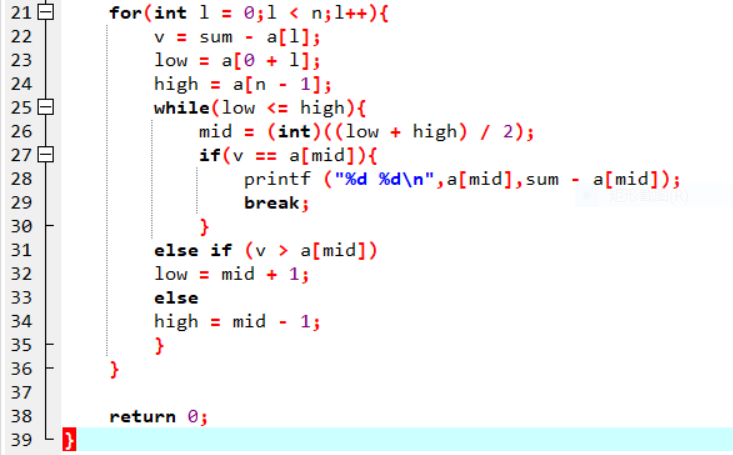
解法三：对数组进行排序，然后使用二分查找法针对arr[i]查找Sum-arr[i]。

要求：

1.根据三种解法给出相应的代码，并给出测试数据。（15分）
解法一：

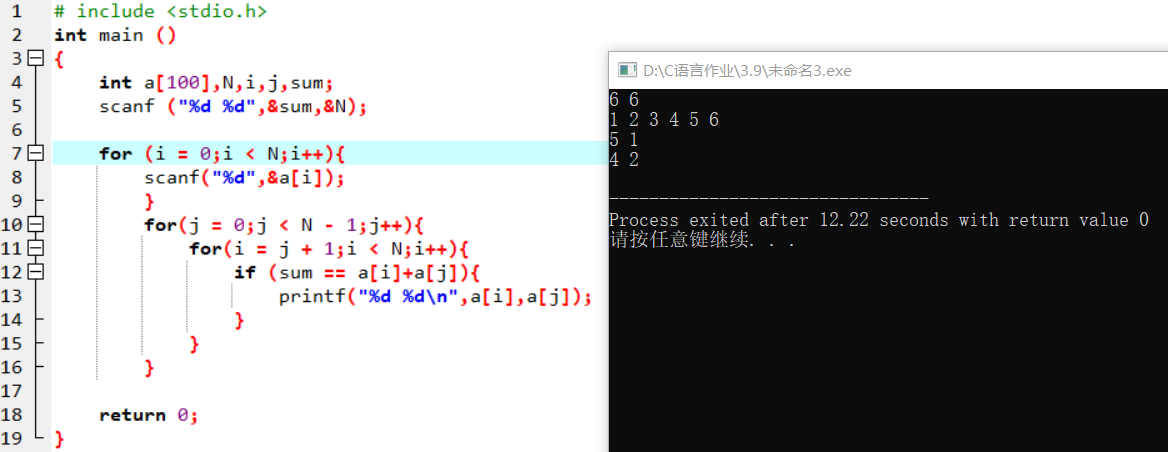
输入数据	输出数据
6 6 1 2 3 4 5 6	5 1 4 2
解法二：
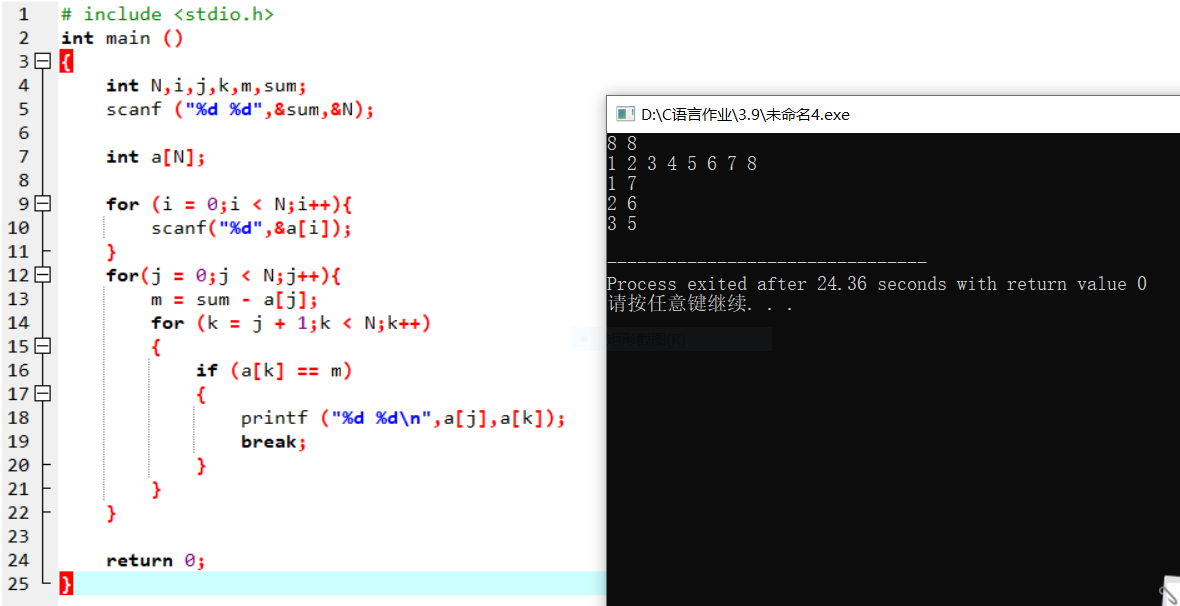输入数据	输出数据
---	---
8 8 1 2 3 4 5 6 7 8	1 7 2 6 3 5
解法三：
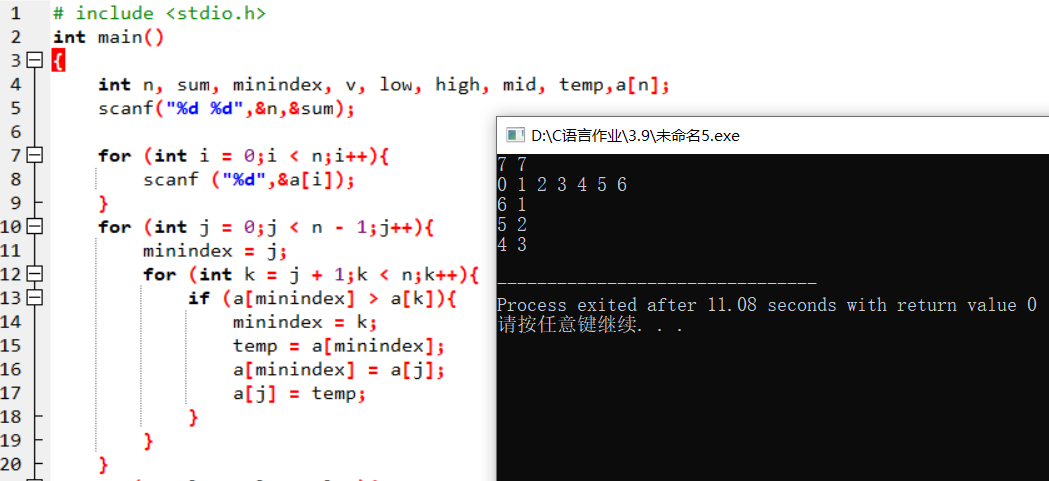输入数据	输出数据
---	---
7 7 0 1 2 3 4 5 6	6 1 5 2 4 3
2.请说明三种算法的区别是什么？你还可以给出更好的算法吗？（10分）

区别：穷举法思路相对简单，但运算量较大，运算时间较长。
      解法二与解法一相似。
      二分查找法解题，虽然思路较复杂，但该方法是最好的，运算时间较前两种解法的运算时间少，提高了解题效率。

2.3 请搜索有哪些排序算法，并用自己的理解对集中排序算法分别进行描述（5分）

排序方法有10种，分别是：冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、桶排序、基数排序。

冒泡排序:重复走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。
选择排序:首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
插入排序：将列表中的每个元素依次和之前排好序的元素进行比较，找到合适的位置插入，使之前有序的列表保持依然有序。
希尔排序：将整个列表根据增量分为若干个子列表分别进行插入排序。随着增量的减小，列表趋于基本有序，当增量为1时，相当再做一次插入排序，使列表有序。
归并排序：将已有序的子序列合并，得到完全有序的序列；
快速排序：通通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，
         整个排序过程可以递归进行，以此达到整个数据变成有序序列。
堆排序：将堆的末端子节点作调整，使得子节点永远小于父节点
计数排序：没有用元素间的比较，它利用元素的实际值来确定它们在输出数组中的位置。
桶排序：利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。
基数排序将整数按位数切割成不同的数字，然后按每个位数分别比较。 

2.4 学习总结（15分）

2.4.1 学习进度条（5分）

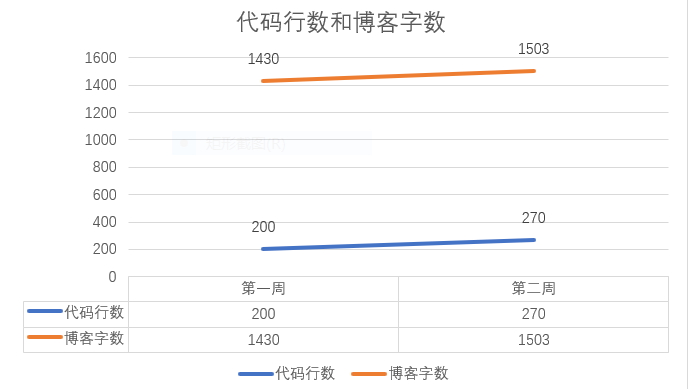
周/日期	这周所花的时间	代码行	学到的知识点简介	目前比较迷惑的问题
第一周	10h	200	测试数据写入文件，使用测试程序检验代码	对相关代码的编写存在问题
第二周	15h	270	排序算法，数组的使用	数组的使用

2.4.2 累积代码行和博客字数（5分））

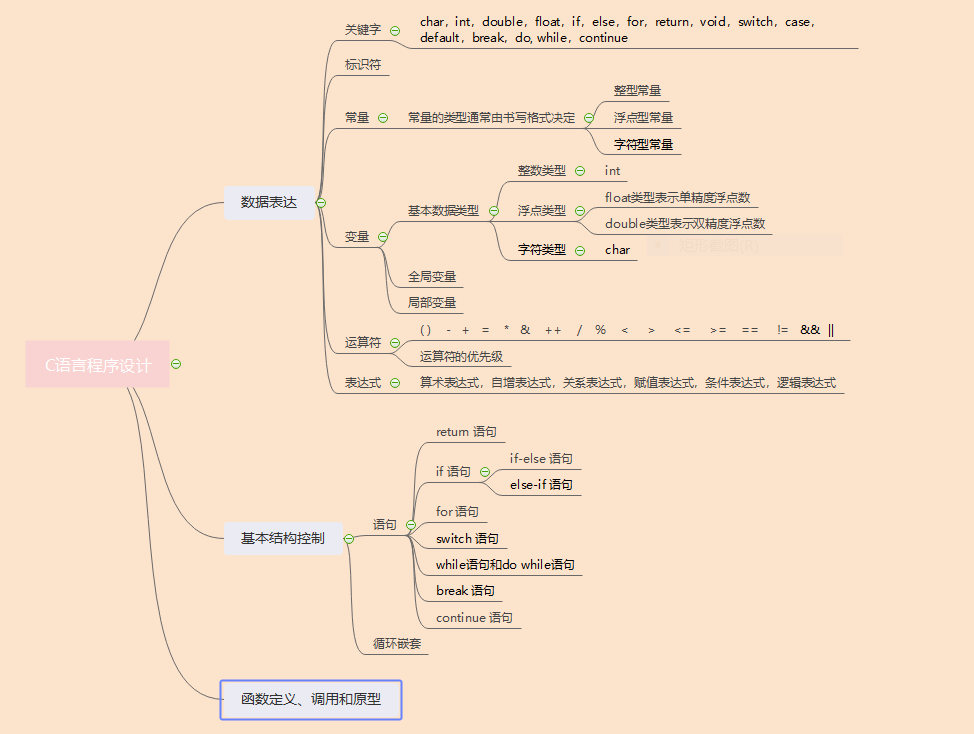
2.4.3 学习内容总结和感悟（5分）

1. 学习内容总结

2. 学习体会
1.本周学习了​数组，学会了更多解决题目的方法。
2.一道题解法很多时，不能全部想到并写出代码。
3.本周学习的知识对我来说比较难，下周应该多进行复习巩固，多多进行编程练习​。
4.多阅读优秀代码，学习优秀之处，学习思路思维，用在自己的代码中。

2.4.4 对冒泡排序的说明和理解（5分）

说明：冒泡排序是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的元素列，依次比较两个相邻的元素，
如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。
理解：冒泡排序法，是从数组的第一个数开始，依次向后比较相邻的两个数；前者比较大时，就将二者换位，这样一次遍历完成后，最大的数就在最后；
之后再从第一个数开始向后比较（不比较最后一个数），依此类推。
第1轮比较需要比较N-1次，比较完了之后，固定1个数在数组最后，剩下前面N-1元素需要比较N-1-1次；
第2轮比较需要比较N-2(N-1-1)次，比较完了之后，固定2个数在数组最后，剩下N-2个元素需要比较N-2-1次；
依次类推：
第i轮比较需要N-i次，比较完了之后，固定i个数在数组最后，剩下N-i个元素需要比较N-i-1次。规律：轮数加次数等于数组长度-1。
由此我们可以得两个变量，一个是比较轮数i，一个是比较次数j，刚由规律得出比较了i轮之后，剩下N-i个元素，需要比较N-i-1,所以j=N-i-1;