乱记

根据牛顿老爷的研究，有广义二项式定理：

\[(ax+b)^{n}=\sum\limits_{k=0}^{+\infty} {n\choose k} (ax)^kp^{n-k} \]

注意到这里的组合数的定义需要拓展，我们约定 \(m\ge 0,n<m\) 时：

\[{n\choose m}=\dfrac{\prod\limits_{i=n-m+1}^{n} i}{m!} \]

简单的说，\(m\) 即选择的个数必须时自然数，而 \(n\) 则没有范围限制，只要是整数即可。

进一步的，我们有：

\[{-n\choose m}=(-1)^m {n+m-1\choose n-1} \]

考虑证明，根据定义易得：

\[{-n\choose m}=\dfrac{\prod\limits_{i=-n-m+1}^{-n} i}{m!}\\ \]

交换一下顺序：

\[(-1)^{-n-(-n-m+1)+1}\dfrac{\prod\limits_{i=n}^{n+m-1}i}{m!} \]

整理一下得到：

\[(-1)^{m}\dfrac{(n+m-1)!}{(n-1)!m!}=(-1)^{m}{n+m-1\choose n-1} \]

这就让我们可以把拓展之后的组合转化成我们熟悉的形式。

需要注意的是，网上一些笔记要求 \(n,m\) 之间满足大小关系，这是不必要的，只要同号就行了。

于是现在我们就可以开心的学习生成函数了，对于生成函数在实际的应用某个东西的生成函数 \(f\)，满足 \([x^i]f(x)\) 为当选择 \(x\) 个时的方案数。

BZOJ3028 食物

承德汉堡选择偶数个那么其生成函数为：

\[f(x)=\sum\limits_{k=0}^{+\infty} x^{2k} \]

取 \(1\) 个的方案数 \([x]f(x)=0\)，而选 \(2\) 个的方案数 \([x^2]f(x)=1\)。

类似的，我们两边同乘 \(x^2\)，那么就得到了：

\[x^2f(x)=\sum\limits_{k=1}^{+\infty} x^{2k} \]

进一步的，可以得到：

\[x^2f(x)=\sum\limits_{k=0}^{+\infty}x^{2k}-1 \]

即：

\[x^2f(x)=f(x)-1 \]

那么就得到了：

\[f(x)=\dfrac{1}{1-x^2} \]

那么 \(f(x)=\dfrac{1}{1-x^2}\) 就是生成函数 \(f(x)=\sum\limits_{k=0}^{+\infty} x^{2k}\) 的封闭形式。

对于剩下的情况，我们逐一考虑。

可乐：

\[f(x)=x+1 \]

鸡腿：

\[f(x)=x^2+x+1 \]

蜜桃多：

\[f(x)=\sum\limits_{k=0}^{+\infty} x^{2k+1}=x\sum\limits_{k=0}^{+\infty} x^{2k}=\dfrac{x}{1-x^2} \]

鸡块：

\[f(x)=\sum\limits_{k=0}^{+\infty} x^{4k}=\dfrac{1}{1-x^4} \]

包子：

\[f(x)=x^3+x^2+x+1 \]

土豆片炒肉：

\[f(x)=x+1 \]

面包：

\[f(x)=\sum\limits_{k=0}^{+\infty} x^{3k}=\dfrac{1}{1-x^3} \]

把上面的封闭形式全部乘起来得到：

\[\dfrac{x}{(x-1)^4}=x(x-1)^{-4} \]

那么根据牛顿老爷的研究，有：

\[x\sum\limits_{k=0}^{+\infty}{-4\choose k}x^k(-1)^{-4-k} \]

于是我们转化一下得到：

\[x\sum\limits_{k=0}^{+\infty}{k+3\choose 3}(-1)^kx^k(-1)^{-4-k} \]

整理一下得到：

\[g(x)=x\sum\limits_{k=0}^{+\infty} {k+3\choose k}x^k \]

于是就得到了答案：

\[[x^n]g(x)={n+3\choose n} \]

做完了。

富强

考试的时候尝试设一种更加神奇的状态，\(f_{i,j,k}\) 表示考虑到了第 \(i\) 个位置，现在有 \(k\) 个逆序对要经过 \(i\)，已经放了 \(j\) 个。

发现直接搞的话会出现放的点不同计算出的逆序对数量也不一样，于是就摆了。

考虑一种更加优雅的设法，我们设 \(f_{i,j}\) 表示考虑了前 \(i\) 个，逆序对数量为 \(j\) 的方案数。

具体的，我们这个前 \(i\) 是一个还没有操作的递增，具体的值不重要。

那么，如果 \(i\) 什么都不干，就有：

\[f_{i,j}\gets f_{i,j}+f_{i,j-1} \]

如果要构成二元环，那么就有转移：

\[f_{i,j}\gets f_{i,j}+\sum\limits_{a=1}^{i-1} f_{i-2,j-(2i-2a-1)} \]

之所以要取 \(f_{i-2,j}\) 是因为避免以前就选择了 \(i,a\)。

一个错误的理解是如果 \(a\) 被换过了依旧是合法的，这样虽然逆序对是对的但是并不满足二元环的要求。

如果让 \(k\) 与 \(n^2\) 同阶，那么这个代码的时间复杂度为 \(O(n^4)\)，考虑优化转移。

套路的，发现下面的 \(\sum\) 里面的第二维是全部在 \(\pmod 2\) 下同于的 \(f\)，于是我们维护一个桶然后做前缀和就行了。

时间复杂度为 \(O(n^3)\)，但是空间不是很够，容易想到滚动一下数组就行了。

感觉这种 DP 数组的设法还是比较常见的，还是自己太撇了。

民主

容易想到去二分，然后去贪心的改。

我们开一个队列，把因为比边上小太多而不合法的位置丢到一个队列里面。

直接更新成合法的最小值，把旁边的点也放到队列里面去。

这样是 \(O(n^2)\) 的，因为可能会出现反复横跳的情况，于是考虑优化。

一种天才的想法是在队列里的点就不再加入了，这样可以获得 \(100\) 分，但是事实上还是错误的。

正确的做法是开一个优先队列把不合法的按照从大到小放进去，这样更新的点就不会再更新了。

但是这样是 \(O(n\log n)\) 的还需要卡常，于是考虑把这些数从大到小丢进去，效果是一样的。

有一种更优雅的方法，其实可以直接正着做一遍然后反着做一遍，这样也是对的。

文明

很破防，容易想到的是把操作设置成未知数然后去解方程。

但是这样是 \(O(n^3)\) 的，于是考虑手动消元找规律。

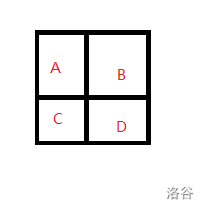
有性质，如果 \(A+D=B+C\)，那么这个是可以通过 \(1,2\) 操作实现的。

我们构造，把 \(D\) 代换成 \(B+C-A\)。

横着分别用 \(-A,-C\)，那么 \((1,1)\) 和 \((1,2)\) 都变成 \(0\) 了，后面两个格子都是 \(B-A\)。

那么我们再给后面一列进行一个 \(A-B\) 的操作，这个 \(2\times 2\) 的东西就全部都是 \(0\) 了。

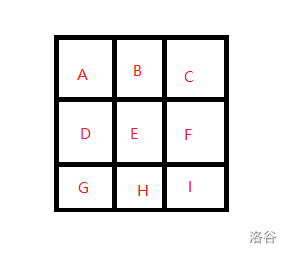
考虑 \(3\times 3\) 的怎么处理，因为 \((1,3)\) 和 \((3,1)\) 斜着可以单独微调，所以我们可以先不考虑他们。

给斜着的也假定一个值。

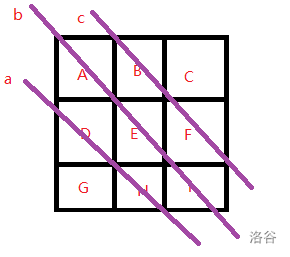
那么如果这些正方形也可以通过 \(1,2\) 操作满足的话，那么就需要满足对角线相等。

于是有：

\[A+E+2\times b=B+D+a+c \]

\[E+I+2\times b=H+F+a+c \]

把两个式子相减得到：

\[A+H+F=I+B+D \]

考虑对于一般的情况，如果 \(3\times 3\) 的性质满足，那么就一定有解，否则无解。

无解是容易理解的，考虑怎么证明有解的情况。

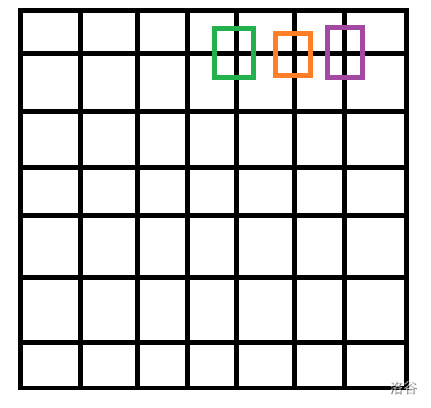
先考虑紫色的正方形，我们令右上的两个对角线不操作，那么为了满足对角线和相等，第 \(3\) 条就确定下来了。

第 \(3\) 条会影响橙色的正方形，于是第 \(4\) 条对角线就也确定了。

以此类推，我们可以把所有的对角线和 \((x,y)\) 满足 \(\min(x,y)\le 2\) 的地方全部确定。

通过构造的方式，我们可以知道这种情况下一定不会有冲突。

我们把方程 \(A+H+F=I+B+D\) 和 \(A+E=B+D\) 联立可以推出新方程：

\[E+I=H+F \]

相当于我们这样的操作就满足了所有的小正方形都是对角线相等的。

现在我们只需要证明所有 \(2\times 2\) 对角线和都相等的情况下一定可以通过 \(1,2\) 操作归零就行了。

这是容易证明的，直接用对角线相等代换就行了。

在进行了对角线的确定之后，就只有 \(1,2\) 操作了，也就成为了 sub2。

感觉这个题目有点脑电波，做出来的也是神人了。