长链剖分学习笔记
长链剖分学习笔记
定义
长链剖分本质上就是另外一种链剖分方式。
重链剖分按照子树的大小划分重儿子和轻儿子,长链剖分则选取到叶子节点距离最大的儿子作为重儿子。
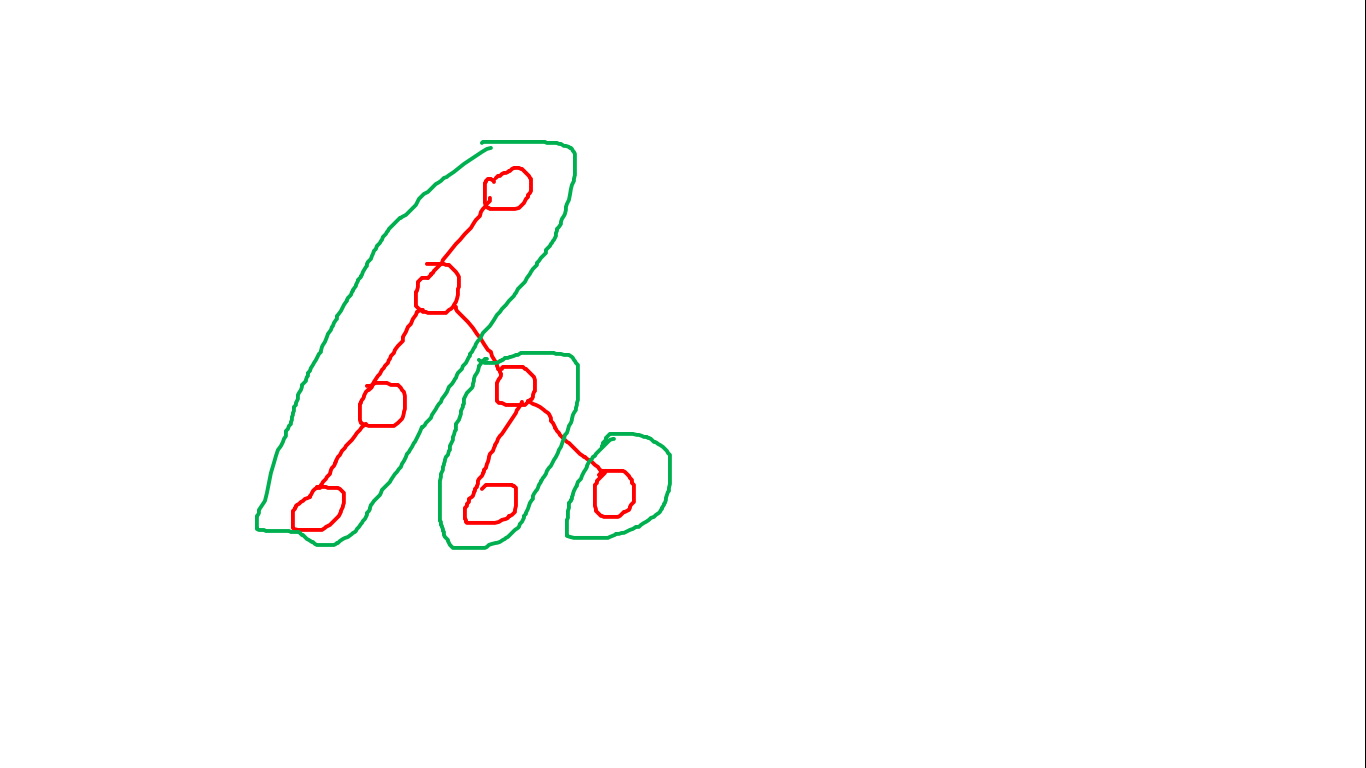
上面的图中绿色的部分就是划分出来的长链。
性质
\(1\)、长链剖分后,所有节点都仅属于一条链。
\(2\)、任意节点到达根节点经过的长链数是 \(\sqrt{n}\) 级别的。
因为每次跳跃到的新链长度不会小于当前链,所以最坏的情况长链的长度就是 \(1,2...\sqrt{n}\)。
应用
求树上k级祖先
长链剖分可以做到 \(O(nlogn)\) 预处理,\(O(1)\) 回答询问。
首先我们对于所有的节点倍增出它的 \(2^k\) 级祖先,同时对于整棵树进行长链剖分。
对于每条链,如果其长度为 \(len\),那么在顶点处记录顶点向上的 \(len\) 个祖先和向下的 \(len\) 个链上的儿子。
查询的时候,我们找到最小的一个 \(2^a\) ,使得 \(2^{a+1} \geq k\),然后对于当前询问的点 \(x\),把 \(x\) 跳到 \(x\) 的 \(2^a\) 级祖先。
此时 \(x\) 所在的长链的长度一定是大于等于 \(2^a\) 的,所以我们就可以利用在链顶处维护的向上和向下的信息快速得到答案。
代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
int n,q,h[maxn],tot=1,fa[maxn][22],dep[maxn],md[maxn],son[maxn],rt,lg[maxn];
struct asd{
int to,nxt;
}b[maxn];
void ad(rg int aa,rg int bb){
b[tot].to=bb;
b[tot].nxt=h[aa];
h[aa]=tot++;
}
#define ui unsigned int
ui s;
inline ui get(ui x) {
x^=x<<13;
x^=x>>17;
x^=x<<5;
return s=x;
}
void dfs1(rg int now){
md[now]=dep[now]=dep[fa[now][0]]+1;
for(rg int i=1;(1<<i)<=dep[now];i++){
fa[now][i]=fa[fa[now][i-1]][i-1];
}
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==fa[now][0]) continue;
dfs1(u);
md[now]=std::max(md[now],md[u]);
if(md[u]>md[son[now]]) son[now]=u;
}
}
int dfn[maxn],dfnc,up[maxn],dow[maxn],tp[maxn];
void dfs2(rg int now,rg int p){
dfn[now]=++dfnc;
dow[dfnc]=now;
up[dfnc]=p;
if(son[now]){
tp[son[now]]=tp[now];
dfs2(son[now],fa[p][0]);
}
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==fa[now][0] || u==son[now]) continue;
tp[u]=u;
dfs2(u,u);
}
}
int cx(rg int now,rg int k){
if(!k) return now;
now=fa[now][lg[k]];
k-=(1<<lg[k]);
k-=dep[now]-dep[tp[now]];
now=tp[now];
if(k>=0) return up[dfn[now]+k];
else return dow[dfn[now]-k];
}
int latans;
int main(){
memset(h,-1,sizeof(h));
n=read(),q=read(),s=read();
for(rg int i=1;i<=n;i++){
fa[i][0]=read();
if(!fa[i][0]) rt=i;
else {
ad(fa[i][0],i);
ad(i,fa[i][0]);
}
}
for(rg int i=2;i<=n;i++){
lg[i]=lg[i/2]+1;
}
dfs1(rt);
tp[rt]=rt;
dfs2(rt,rt);
rg long long ans=0;
rg int aa,bb;
for(rg int i=1;i<=q;i++){
aa=(get(s)^latans)%n+1;
bb=(get(s)^latans)%dep[aa];
latans=cx(aa,bb);
ans^=1LL*i*latans;
}
printf("%lld\n",ans);
return 0;
}
优化DP
一些和深度有关的 \(dp\) 可以用长链剖分优化至 \(O(n)\),因为每一条长链的贡献只会在链顶被计算,其它的情况都是直接继承。
因为二维数组开不下,所以一般都要拿一个内存池动态分配内存。
例题:P5904 [POI2014]HOT-Hotels 加强版
\(f_{i,j}\)为满足 \(x\) 在 \(i\) 的子树中且 \(d(x, i) = j\) 的 \(x\) 的个数,\(g_{i,j}\) 为满足 \(x,y\) 在 \(i\) 的子树中且 \(d(\operatorname{lca}(x, y), x) = d(\operatorname{lca}(x, y), y) = d(\operatorname{lca}(x, y), i) + j\) 的无序数对 \((x,y)\) 的个数。
转移的时候大力分类讨论。
统计答案时考虑在每一个节点处匹配的点对,可以直接由 \(g_{i,0}\) 转移过来,也可以由 \(i\) 两个儿子 \(x,y\) 转移而来,即 \(f_{x,j-1} \times f_{y,j+1}\)。
\(g_{i,j}\) 可以直接由 \(g_{x,j+1}\) 继承,也可以由 \(f_{x,j-1} \times f_{y,j-1}\) 转移。
最后的 \(f\) 数组直接由 \(f_{x,j-1}\) 转移到 \(f_{i,j}\) 即可。
代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e5+5;
typedef long long ll;
int n,h[maxn],tot=1,md[maxn],son[maxn];
struct asd{
int to,nxt;
}b[maxn<<1];
void ad(rg int aa,rg int bb){
b[tot].to=bb;
b[tot].nxt=h[aa];
h[aa]=tot++;
}
void dfs1(rg int now,rg int lat){
md[now]=1;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==lat) continue;
dfs1(u,now);
md[now]=std::max(md[now],md[u]+1);
if(md[u]>md[son[now]]) son[now]=u;
}
}
ll *f[maxn],*g[maxn],buf[maxn<<2],*o=buf,ans;
void dfs2(rg int now,rg int lat){
if(son[now]){
f[son[now]]=f[now]+1;
g[son[now]]=g[now]-1;
dfs2(son[now],now);
}
f[now][0]=1;
ans+=g[now][0];
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==lat || u==son[now]) continue;
f[u]=o;
o+=(md[u]<<1);
g[u]=o;
o+=(md[u]<<1);
dfs2(u,now);
for(rg int j=0;j<=md[u];j++){
ans+=f[now][j]*g[u][j+1];
if(j) ans+=g[now][j]*f[u][j-1];
}
for(rg int j=0;j<=md[u];j++){
if(j) g[now][j]+=f[now][j]*f[u][j-1];
g[now][j]+=g[u][j+1];
}
for(rg int j=0;j<=md[u];j++){
if(j) f[now][j]+=f[u][j-1];
}
}
}
int main(){
memset(h,-1,sizeof(h));
n=read();
rg int aa,bb;
for(rg int i=1;i<n;i++){
aa=read(),bb=read();
ad(aa,bb);
ad(bb,aa);
}
dfs1(1,0);
f[1]=o;
o+=(md[1]<<1);
g[1]=o;
o+=(md[1]<<1);
dfs2(1,0);
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号