联赛前数学知识
PART ONE 质数
一、质数的判定
1、定义
若一个正整数无法被除了 \(1\) 和它自身之外的任何自然数整除,则称该数为质数(或素数),否则称该正整数为合数。
在整个自然数集合中,质数的数量不多,分布比较稀疏,对于一个足够大的整数 \(N\),不超过 \(N\) 的质数大约有 \(\frac{N}{lnN}\) 个,即每 \(lnN\) 个数中大约有 \(1\) 个质数。
2、一些性质
\((1)\)、两个质数一定是互质数。例如,\(2\)与\(7\)、\(13\)与\(19\)。
\((2)\)、一个质数如果不能整除另一个合数,这两个数为互质数。例如,\(3\)与\(10\)、\(5\)与\(26\)。
\((3)\)、\(1\)不是质数也不是合数,它和任何一个自然数在一起都是互质数。如\(1\)和\(9908\)。
\((4)\)、相邻的两个自然数是互质数。如\(15\)与\(16\)。
\((5)\)、相邻的两个奇数是互质数。如\(49\)与\(51\)。
\((6)\)、\(2\)和任意奇数互质
3、试除法
扫描\(2\sim \sqrt{n}\)之间的所有整数,依次检查它们能否整除\(n\),若都不能整除,则\(n\)是质数,否则\(n\)是合数。
代码
bool is_prime(int n){
if(n<2) return 0;
int m=sqrt(n);
for(int i=2;i<=m;i++){
if(n%i==0) return 0;
}
return 1;
}
二、质数的筛法
1、Eratosthenes筛法
\(Eratosthenes\) 筛法基于这样的想法:任意整数 \(x\) 的倍数\(2x\),\(3x\),…都不是质数。根据质数的定义,上述命题显然成立。
我们可以从\(2\)开始,由小到大扫描每个数\(x\),把它的倍数\(2x\),\(3x\),…,\([\frac{N}{x}] \times x\)标记为合数。
当扫描到一个数时,若它尚未被标记,则它不能被\(2 \sim x-1\)之间的任何数整除,该数就是质数。
时间复杂度\(O(NloglogN)\)
代码
const int maxn=1e6+5;
bool vis[maxn];
void get_prime(int n){
for(int i=2;i<=n;i++){
if(vis[i]) continue;
printf("%d\n",i);
int m=n/i;
for(int j=i;j<=m;j++){
vis[i*j]=1;
}
}
}
2、线性筛
埃氏筛中,每个合数会被多次标记
而在线性筛中,每个合数只会被它的最小质因子筛一次,因此时间复杂度为\(O(N)\)。
代码
const int maxn=1e6+5;
int pri[maxn];
bool not_prime[maxn];
void xxs(int n){
not_prime[0]=not_prime[1]=1;
for(int i=2;i<=n;++i){
if(!not_prime[i]){
pri[++pri[0]]=i;
}
for (int j=1;j<=pri[0] && i*pri[j]<=n;j++){
not_prime[i*pri[j]]=1;
if(i%pri[j]== 0) break;
}
}
}
三、质因数分解
1、算术基本定理
任何一个大于\(1\)的正整数都能唯一分解为有限个质数的乘积,可写作:
其中\(c_i\)都是正整数,\(p_i\)都是质数,且满足\(p_1<p_2<…<p_m\)
2、试除法
结合质数判定的“试除法”和质数筛选的“\(Eratosthenes\)筛法”,我们可以扫描\(2\sim\sqrt{n}\)的每个数\(d\),若\(d\)能整除\(N\),则从\(N\)中除掉所有的因子\(d\),同时累计除去的\(d\)的个数。
因为一个合数的因子一定在扫描到这个合数之前就从\(N\)中被除掉了,所以在上述过程中能整除\(N\)的一定是质数。
最终就得到了质因数分解的结果,易知时间复杂度为\(O(\sqrt{n})\)。
特别地,若\(N\)没有被任何\(2\sim\sqrt{n}\)的数整除,则\(N \)是质数,无需分解。
代码
const int maxn=1e6+5;
int cnt[maxn],pri[maxn];
void div(int n){
int m=sqrt(n);
for(int i=2;i<=m;i++){
if(n%i==0){
pri[++pri[0]]=i,cnt[pri[0]]=0;
while(n%i==0){
n/=i;
cnt[pri[0]]++;
}
}
}
if(n>1){
pri[++pri[0]]=n;
cnt[pri[0]]=1;
}
for(int i=1;i<=pri[0];i++){
printf("%d %d\n",pri[i],cnt[i]);
}
}
PART TWO 约数
一、定义
若整数\(n\)除以整数\(d\)的余数为\(0\),即\(d\)能整除\(n\),则称\(d\)是\(n\)的约数,\(n\)是\(d\)的倍数,记为\(d|n\)。
二、算术基本定理的推论
在算术基本定理中,若正整数\(N\)被唯一分解为
其中\(c_i\)都是正整数,\(p_i\)都是质数,且满足\(p_1<p_2...<p_m\),
则N的正约数集合可写作:
其中\(0 \leq b_i \leq c_i\)
\(N\)的正约数的个数为
\(N\)的所有正约数的和为
三、求N的正约数集合:试除法
扫描\(d=1\sim\sqrt{N}\),尝试\(d\)能否整除\(N\),若能整除,则\(\frac{N}{d}\)也是\(N\)的约数。时间复杂度为\(O(\sqrt{N})\)
代码过水,就不放了
试除法的推论
一个整数\(N\)的约数个数上界为\(2\sqrt{n}\)
四、求1~N每个数的正约数集合——倍数法
const int maxn=1e6+5;
std::vector<int> g[maxn];
void div(int n){
for(int i=1;i<=n;i++){
int m=n/i;
for(int j=1;j<=m;j++){
g[i*j].push_back(i);
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<g[i].size();j++){
printf("%d ",g[i][j]);
}
printf("\n");
}
}
倍数法推论
\(1\sim N\)每个数的约数个数的总和大约为\(NlogN\)。
五、最大公约数
定义:一组数的公约数,是指同时是这组数中每一个数的约数的数。而最大公约数,则是指所有公约数里面最
大的一个,常缩写为 \(gcd(Greatest\ Common\ Divisor)\)。
1、辗转相除法(欧几里得法)求两个数的最大公因数
证明
任意\(a\),\(b\)属于\(N+\),\(a \geq b\),有\(gcd(a,b)=gcd(b,a-b)=gcd(a,a-b)\)。
任意\(a\),\(b\)属于\(N+\),有\(gcd(2a,2b)=2gcd(a,b)\)。
根据最大公约数的定义,后者显然成立,我们主要证明前者。
对于\(a\),\(b\)的任意公约数d,因为\(d|a,d|b\),所以\(d|(a-b)\)。因此\(d\)也是\(b,a-b\)的公约数,反之亦成立。
故\(a,b\)的公约数集合与\(b,a-b\)的公约数集合相同。于是它们的最大公约数自然也相等,对于\(a,a-b\)同理。
代码
int getgcd(int aa,int bb){
if(bb==0) return aa;
return getgcd(bb,aa%bb);
}
时间复杂度\(O(log(a+b))\)
2、辗转相减法(尼考曼彻斯法)求两个数的最大公因数
证明
若\(a<b\),则\(gcd(b,a mod b)=gcd(b,a)=gcd(a,b)\),命题成立。
若\(a>b\),不妨设\(a=q \times b+r\),其中\(0 \leq r<b\)。显然\(r=a mod b\)。
对于\(a,b\)的任意公约数\(d\),因为\(d|a,d|q \times b\),故\(d|(a-q \times b)\),即\(d|r\),因此\(d\)也是\(b\),\(r\)的公约数。反之亦成立。
故\(a,b\)的公约数集合与\(b,a modb\)的公约数集合相同。于是它们的最大公约数自然也相等。
代码
int getgcd(int aa,int bb){
return aa==bb ? aa:getgcd(aa>bb ? aa-bb:aa, bb>aa ? bb-aa:bb);
}
复杂度基本保持在\(O(logn)\),不过有概率退化成\(O(n)\)。
如果写高精度的话,用这一种会比较方便。
3、求两个数的最小公倍数
\(lcm(aa,bb)=aa\times bb \div gcd(aa,bb)\)
4、求多个数的最大公因数或最小公倍数
两两相求就可以了
5、扩展欧几里得定理
定义
对于不完全为 \(0\) 的整数 \(a\),\(b\),\(gcd(a,b)\)表示 \(a\),\(b\) 的最大公约数。那么一定存在整数 \(x\),\(y\) 使得 \(gcd(a,b)=ax+by\)。
求法
int exgcd(int aa,int bb,int &x,int &y){
if(bb==0){
x=1,y=0;
return aa;
}
int ans=exgcd(bb,aa%bb,x,y);
int t=x;
x=y;
y=t-aa/bb*y;
return ans;
}
证明
设\(ax+by=t\),当\(b=0\)时,\(t=a\),显然有\(x=1,y=0\)
设\(ax_1+by_1=gcd(a,b),bx_2+(a\%b)y_2=gcd(b,a\%b)\)
由于\(gcd(a,b)=gcd(b,a \% b)\),
联立有:\(ax_1+by_1=bx_2+(a\%b)y_2\)
\(ax_1+by_1=bx_2+(a-a/b \times b)y_2\)
将\(a\),\(b\)示为未知数:整理等式
\(ax_1+by_1=ay_2+b(x_2-y_2(a/b))\)
\(x_1=y_2, y_1=x_2-(a/b)*y_2\)
一般解
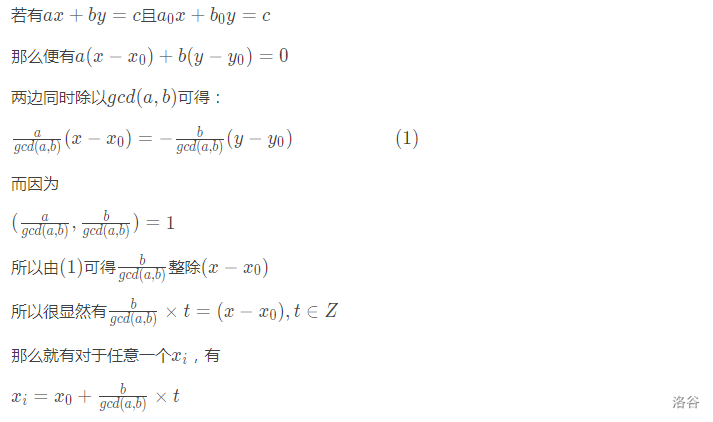
六、线性筛约数个数与约数和
1、线性筛约数个数
//线性筛约数个数,F表示约数个数,T表示最小质因子的个数
inline void GetPrime(){
F[1]=1;//不要忘记1
for(int i=2;i<=n;i++){
if(!done[i]){
Prime[++tot]=i;
F[i]=2;T[i]=1;//i是约数,然后显然呢
}
for(int j=1;j<=tot&&i*Prime[j]<=n;j++){
done[i*Prime[j]]=1;
if(i%Prime[j]==0){//i又包含了最小质因子,当然先除掉在乘回来
F[i*Prime[j]]=F[i]/(T[i]+1)*(T[i]+2);
T[i*Prime[j]]=T[i]+1;
break;
}
F[i*Prime[j]]=F[i]*2;//新来的质因子你好啊?和任意一个已知的约数都可以合体呢
T[i*Prime[j]]=1;
}
}
}
2、线性筛约数和
//线筛约数和,F表示约数和
inline void GetPrime(){
F[1]=1;//同理
for(int i=2;i<=500000;i++){
if(!done[i]){
Prime[++tot]=i;
F[i]=i+1;//孤独的1和i
}
for(int j=1;j<=tot&&i*Prime[j]<=500000;j++){
done[i*Prime[j]]=1;
if(i%Prime[j]==0){//一个简单的小容斥,只包含一个Prime[j]的约数算了两次
F[i*Prime[j]]=F[i]*F[Prime[j]]-Prime[j]*F[i/Prime[j]];
break;
}
else F[i*Prime[j]]=F[i]*F[Prime[j]];//又是一对一对又一对
}
}
}
七、互质与欧拉函数
1、定义:
任意\(a\),\(b\)属于\(N+\),若\(gcd(a,b)=1\),则称\(a\),\(b\)互质。
对于三个数或更多个数的情况,我们把\(gcd(a,b,c)=1\)的情况称为\(a\),\(b\),\(c\)互质;
把\(gcd(a,b)=gcd(a,c)=gcd(b,c)=1\)称为\(a\),\(b\),\(c\)两两互质。后者显然是一个更强的条件。
2、欧拉函数
定义
\(1\sim N\)中与\(N\)互质的数的个数被称为欧拉函数,记为\(φ(N)\)。
若在算术基本定理中,
\(N=p_1^{c_1} \times p_2^{c_2}...p_m^{c_m}\)
则:
\(φ(N)=N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times ... \times \frac{p_m-1}{p_m}=N \times \prod_{p|N} (1-\frac{1}{p})\)(其中\(p\)为质数)
证明:
设\(p\)是\(N\)的质因子,\(1 \sim N\)中\(p\)的倍数有\(p\),\(2p\),\(3p\)…,\((N/p) \times p\),共\(N/p\)个。
同理,若\(q\)也是\(N\)的质因子,则\(1 \sim N\)中\(q\)的倍数有\(N/q\)个。
如果我们把这\(N/p+N/q\)个数去掉,那么\(p \times q\)的倍数被排除了两次,需要加回来一次。
因此,\(1 \sim N\)中不与\(N\)含有共同质因子\(p\)或\(q\)的数的个数为:
\(N-\frac{N}{p}-\frac{N}{q}+\frac{N}{p \times q}=N\times (1-\frac{1}{p}-\frac{1}{q}+\frac{1}{p\times q})=N \times (1-\frac{1}{p}) \times (1-\frac{1}{q})\)
类似地,可以在\(N\)的全部质因子上使用容斥原理,即可得到\(1 \sim N\)中不与\(N\)含有任何共同质因子的数的个数,也就是与\(N\)互质的数的个数。
根据欧拉函数的计算式,我们只需要分解质因数,即可顺便求出欧拉函数。
性质
\(n\) 的所有因子的欧拉函数的和为 \(n\) 。
即 \(\sum_{d|n} \varphi(d)=n\)
3、欧拉函数求法
单个欧拉函数值
int getphi(int xx){
int ans=xx;
int m=(int)sqrt(xx+0.5);
for(int i=2;i<=m;i++){
if(xx%i==0){
ans=ans/i*(i-1);
while(xx%i==0) xx/=i;
}
}
if(xx>1) ans=ans/xx*(xx-1);
return ans;
}
时间复杂度\(O(\sqrt{n})\)
线性筛求1~n的欧拉函数值
void getphi(int n){
phi[1]=1;
for(int i=1;i<=n;i++){
if(!isnot_prime[i]){
prime[++prime[0]]=i;
phi[i]=i-1;
}
for(int j=1;j<=prime[0] && i*prime[j]<=n;j++){
isnot_prime[i*prime[j]]=1;
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];
//将i*pri[j]分成pri[j]段,每一段都有phi[i]个数与其互质
break;
} else {
phi[i*prime[j]]=phi[i]*(prime[j]-1);
//根据积性函数性质
}
}
}
}
时间复杂度\(O(n)\)
积性函数
如果 \(a\),\(b\) 互质,并且有 \(f(ab)=f(a) \times f(b)\),那么就说函数为积性函数。
PART THREE 同余
一、同余类与剩余系
1、同余
定义
若整数\(a\),\(b\)除以正整数\(m\)的余数相等,则称 \(a\),\(b\) 模 \(m\)同余,记为 \(a≡b(modm)\)
2、同余类 & 剩余系
定义
对于任意正整数 \(a(0\leq a \leq m-1)\)
集合 \(\{a+km\}(k=0,1,2,3...)\) 模 \(m\) 同余,余数为 \(a\) ,则称该集合为一个模 \(m\) 的同余类。
显然,\(m\) 的同余类一共有\(m\)个,它们构成 \(m\) 的完全剩余系。
二、一些定理
1、费马小定理
内容
若\(p\)为素数,对于任意整数 \(a\),有
\(a^{p-1}≡1(mod p)\)
也可以写成 \(a^p≡ a(mod p)\)
2、欧拉定理
内容
若正整数 \(a\),$ n$ 互质,则有 \(a^{φ(n)}≡a(mod p)\),其中 \(φ(n)\) 是欧拉函数
扩展欧拉定理
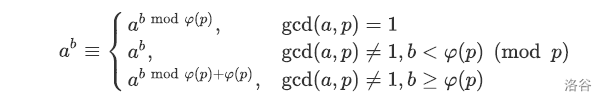
3、二次探测定理
内容
若 \(p\) 为质数且\(x∈(0,p)\),则方程 \(x^2≡1(mod p)\) 的解为 \(x_1=1\),\(x_2=p-1\)。
4、裴蜀定理
内容
方程 \(ax+by=c\)(\(a\)为正整数,\(b\)为正整数)有解的充要条件是 \(gcd(a,b)|c\)。
注意其中 \(c\) 必须大于等于 \(gcd(a,b)\)。
三、乘法逆元
1、定义
若\((a \times x) ≡1(mod b)\)
则称 \(x\) 为 \(a\)在模 \(b\)意义下的乘法逆元,记为 \(a^{-1}\)。
注意:并非所有的情况下都存在乘法逆元,但是当 \(gcd(a,b)=1\)即\(a,b\)互质时,存在乘法逆元
2、费马小定理求逆元
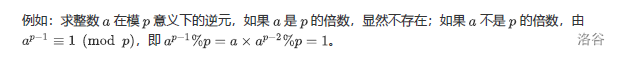
3、 欧拉定理求逆元

4、 扩展欧几里得求逆元

5、线性求逆元

6、比较
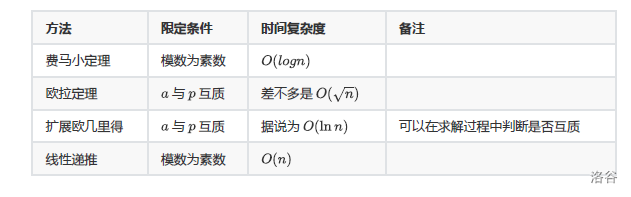
注意:求逆元往往涉及大量的乘法,所以运算的时候一定要注意是否需要用到 long long。
四、中国剩余定理(CRT)
1、基本内容
中国剩余定理主要用于求解模数互质的一组线性同余方程的解。
设\(m_1,m_2,m_3,....,m_n\)为两两互质的整数
\(m=\prod _{i=1}^{n}m_i,M_i=m/m_i\)
\(t_i\)是线性同余方程 \(M_it_i \equiv 1(mod\ m_i)\) 的一个解
对于任意的\(n\)个整数\(a_1,a_2,a_3,...,a_n\),方程组
\(\begin{cases} x\equiv a_1(mod\ m_1)\\x\equiv a_2(mod\ m_2)\\...\\x\equiv a_n(mod\ m_n)\end{cases}\)
有整数解,解为\(x=\sum _{i=1}^na_iM_it_i\)
2、证明
因为\(M_i=m/m_i\)是除\(m_i\)之外所有模数的倍数
所以\(\forall k \neq i,a_iM_it_i \equiv0(mod\ m_k)\)
又因为\(a_iM_it_i \equiv a _i (mod\ m_i)\)
所以代入\(x=\sum_{i=1}^na_iM_it_i\),原方程组成立
3、通解
\(x=x+k\times m\)
\(k\)为整数
4、代码
#include<cstdio>
const int maxn=25;
#define int long long
int ex_gcd(int aa,int bb,int &x,int &y){
if(bb==0){
x=1,y=1;
return aa;
}
int ans=ex_gcd(bb,aa%bb,x,y);
int t=x;
x=y;
y=t-aa/bb*y;
return ans;
}
int a[maxn],b[maxn],n,T=1,t[maxn],val[maxn];
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld",&a[i],&b[i]);
T*=a[i];
}
for(int i=1;i<=n;i++){
int xx,yy;
t[i]=T/a[i];
ex_gcd(t[i],a[i],xx,yy);
val[i]=xx;
}
int ans=0;
for(int i=1;i<=n;i++){
ans=ans+b[i]*val[i]*t[i];
}
ans=(ans%T+T)%T;
printf("%lld\n",ans);
return 0;
}
PART FOUR 高斯消元
一、内容
高斯消元是一种求解线性方程组的方法
所谓线性方程组,是由\(M\)个\(N\)元一次方程共同构成的
线性方程组的所有系数可以写成一个\(M\)行\(N\)列的系数矩阵
再加上每个方程等号右侧的常数,可以写成一个\(M\)行\(N+1\)列的增广矩阵
求解这种方程组的步骤可以概括成对增广矩阵的三类操作
\(1\)、用一个非零的数乘某一行
\(2\)、把其中一行的若干倍加到另一行上
\(3\)、交换两行的位置
如果最后得到的矩阵中出现某一行的系数全为\(0\),但是常数不为\(0\),则说明方程无解
如果出现某一行的系数全部为\(0\),并且常数也为\(0\),则说明方程有无穷多解
二、代码
#include<cstdio>
#include<cmath>
#include<iostream>
typedef double db;
const int maxn=105;
const db eps=1e-20;
db mp[maxn][maxn],ans[maxn],mmax;
int n,jl,now=1;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++){
scanf("%lf",&mp[i][j]);
}
}
for(int i=1;i<=n;i++){
mmax=0;
for(int j=now;j<=n;j++){
if(fabs(mp[j][i])>fabs(mmax)){
mmax=mp[j][i];
jl=j;
}
}
if(fabs(mmax)<eps) continue;
if(now!=jl) std::swap(mp[now],mp[jl]);
for(int j=i+1;j<=n+1;j++){
mp[now][j]/=mp[now][i];
}
mp[now][i]=1.0;
for(int j=now+1;j<=n;j++){
double cs=mp[j][i];
for(int k=i;k<=n+1;k++){
mp[j][k]-=mp[now][k]*cs;
}
}
now++;
}
bool pd=0;
for(int i=1;i<=n;i++){
int ncnt=0;
for(int j=1;j<=n;j++){
if(std::fabs(mp[i][j])<eps) ncnt++;
}
if(ncnt==n && std::fabs(mp[i][n+1]>eps)){
printf("-1\n");
return 0;
} else if(ncnt==n){
pd=1;
}
}
if(pd){
printf("No Solution\n");
return 0;
}
ans[n]=mp[n][n+1];
for(int i=n-1;i>=1;i--){
ans[i]=mp[i][n+1];
for(int j=i+1;j<=n;j++){
ans[i]-=(mp[i][j]*ans[j]);
}
}
for(int i=1;i<=n;i++){
printf("%.2lf\n",ans[i]);
}
return 0;
}
PART FIVE 组合数
一、 定义
从\(n\)个不同元素中,任取\(m(m≤n)\)个元素并成一组,叫做从\(n\)个不同元素中取出\(m\)个元素的一个组合;从\(n\)个不同元素中取出\(m(m≤n)\)个元素的所有组合的个数,叫做从\(n\)个不同元素中取出\(m\)个元素的组合数。
二、求法
1、 公式法
计算组合数的一般公式:
\(C^m_n=\frac{n!}{m!(n-m)!}\)
其中\(n!=1\times2\times\cdots\times nn\)
特别地,定义\(0!=1\)
如果模数为质数,我们就可以提前处理出阶乘的逆元和逆元的阶乘
#define int long long
int getC(int n,int m){
if(m==0) return 1ll;
return jc[n]%mod*jcc[n-m]%mod*jcc[m]%mod;
}
signed main(){
ny[1]=1;
for(int i=2;i<=n;i++){
ny[i]=(mod-mod/i)*ny[mod%i]%mod;
}
jc[0]=1;
for(int i=1;i<=n;i++){
jc[i]=jc[i-1]*i%mod;
}
jcc[0]=1;
for(int i=1;i<=n;i++){
jcc[i]=jcc[i-1]*ny[i]%mod;
}
int n,m;
scanf("%lld%lld",&n,&m);
printf("%lld\n",getC(n,m));
}
2、 递推法
针对大多数仅仅是利用组合数求解问题的题目运用递推法打表,不仅方便,而且可以稳稳地控制复杂度,对于需要多次引用组合数的题目效果极佳:
基于组合数公理性质:\(C^m_n=C^{n-m}_n\)
(请大家务必记住此公式,由此在考场上灵活使用)
推得:\(C^m_n=C^{m-1}_{n-1}+C^m_{n-1}\)
由这个递推公式就可以熟练的写出组合数代码,但要注意初始化:
\(C^0_0=0\)
\(C^i_0=C^1_0=C^1_1=1\)( \(i\)为自然数 )
同时,把表打出来后,我们会发现———这就是杨辉三角,这个三角可以解决很多问题,记住打印三角的方法也可以打出组合数。
c[0][0]=c[1][0]=c[1][1]=1;
for(int i=2;i<=2000;i++){
c[i][0]=1;
for(int j=1;j<=i;j++){
c[i][j]=c[i-1][j-1]+c[i-1][j];
}
}
三、卢卡斯定理
1、定理内容
普通的求组合数一般提前预处理出来阶乘的逆元。
但是当数据范围巨大的时候我们无法进行预处理,或者说给的\(mod\)很烂的时候,这时候我们就要用到卢卡斯定理来解决这个问题。
若\(p\)是质数,则对于任意整数\(1 \leq m \leq n\),有
时间复杂度\(O(p+log_pn)\)
2、代码
#include<cstdio>
const int maxn=1e5+5;
int t,n,m,p,ny[maxn],jc[maxn],jcc[maxn];
int get_C(int nn,int mm){
if(nn<mm) return 0;
return 1LL*jc[nn]*jcc[mm]%p*jcc[nn-mm]%p;
}
int lks(int aa,int bb){
if(bb==0) return 1;
return 1LL*lks(aa/p,bb/p)*get_C(aa%p,bb%p)%p;
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%d%d%d",&n,&m,&p);
ny[1]=1;
for(int i=2;i<=p;i++){
ny[i]=1LL*(p-p/i)*ny[p%i]%p;
}
jcc[0]=jc[0]=1;
for(int i=1;i<=p;i++){
jc[i]=1LL*jc[i-1]*i%p;
jcc[i]=1LL*jcc[i-1]*ny[i]%p;
}
int ans=lks(n+m,n);
printf("%d\n",ans);
}
return 0;
}
四、卡特兰数
1、基本模型
有一个长度为 \(2n\)的\(01\)序列,其中\(1,0\)各 \(n\)个,要求对于任意的整数 $k \in [1,2n] $,数列的前 \(k\)个数中,\(1\)的个数不少于\(0\)
满足条件的序列的数量为
另一种形式
递推式
2、证明
3、推论
以下问题都与卡特兰数有关
1、\(n\)个左括号和\(n\)个右括号组成的合法括号序列的数量为\(Cat_n\)
2、\(1,2,...,n\)经过一个栈,形成的合法出栈序列的数量为\(Cat_n\)
3、\(n\)个节点构成的不同二叉树的数量为\(Cat_n\)
4、在平面直角坐标系上,每一步只能向上或向右走,从\((0,0)\)走到\((n,n)\)并且除两个端点外不接触直线\(y=x\)的路线数量为\(2Cat_n-1\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号