Splay学习笔记
一、二叉排序树
1、定义
二叉排序树\((Binary\ Sort\ Tree)\),又称二叉查找树\((Binary\ Search\ Tree)\),亦称二叉搜索树。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1、若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2、若右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3、左、右子树也分别为二叉排序树。
下面的这幅图就是一个二叉排序树
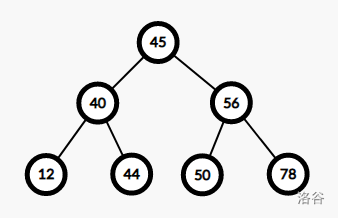
2、二叉排序树的查找
二叉排序树查找在在最坏的情况下,需要的查找时间取决于树的深度:
1、当二叉排序树接近于满二叉树时,其深度为\(log_2n\),因此最坏情况下的查找时间为\(O(log_2n)\),与折半查找是同数量级的。
2、但是当二叉树如下图所示形成单枝树时,其深度为\(n\),最坏情况下查找时间为\(O(n)\),与顺序查找属于同一数量级。
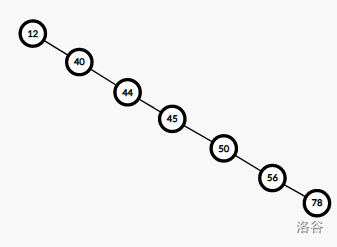
所以,为了保证二叉排序树的查找有较高的查找速度,希望该二叉树接近于满二叉树
或者二叉树的每一个节点的左、右子树深度尽量相等
而\(Splay\)可以很好地解决这一问题
二、Splay
伸展树(Splay Tree),也叫分裂树,是一种二叉排序树,它能在\(O(log n)\)内完成插入、查找和删除操作。它由丹尼尔·斯立特\(Daniel\ Sleator\) 和 罗伯特·恩卓·塔扬\(Robert\ Endre\ Tarjan\) 在1985年发明的。
1、结构体定义
struct trr{
int son,ch[2],fa,cnt,val;
}tr[maxn];
其中\(son\)为儿子数量
\(ch[0]\)为左儿子的编号,\(ch[1]\)为右儿子的编号
\(fa\)为当前节点的父亲节点
\(cnt\)为当前节点的数量
\(val\)为当前节点的权值
2、旋转操作
旋转操作是\(Splay\)中的基本操作
每次有新节点加入、删除或查询时,我们都将其旋转至根节点
这样可以保持\(BST\)的平衡
我们拿实际的图来演示一下
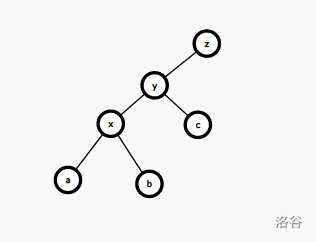
在这幅图中,\(x\)是\(y\)的左儿子,而我们想要将\(x\)旋转至\(y\)的位置
首先,根据\(BST\)的性质,\(x<y\)
因此旋转后,\(y\)应该变为\(x\)的右儿子
那\(x\)原来的右儿子\(b\)呢
根据性质有\(x<b<y\),而\(y\)在旋转后恰好没有左儿子,因此我们让\(b\)当\(y\)的左儿子
\(y\)的右儿子\(c\)和\(x\)的左儿子\(b\)保持不变即可
旋转后的图变成了下面这个样子

旋转后的图仍满足\(BST\)的性质
但实际上,我们只列举出了\(4\)种情况中的一种
1、\(y\)是\(z\)的左儿子,\(x\)是\(y\)的左儿子
2、\(y\)是\(z\)的左儿子,\(x\)是\(y\)的右儿子
3、\(y\)是\(z\)的右儿子,\(x\)是\(y\)的右儿子
4、\(y\)是\(z\)的右儿子,\(x\)是\(y\)的左儿子
如果对于每一种情况我们都分别枚举一遍会很麻烦
根据\(yyb\)神犇的总结
1、\(x\)变到原来\(y\)的位置
2、\(y\)变成了 \(x\)原来在\(y\)的相对 的那个儿子
3、\(y\)的非\(x\)的儿子不变 \(x\)的 \(x\)原来在\(y\)的 那个儿子不变
4、\(x\)的 \(x\)原来在\(y\)的 相对的 那个儿子 变成了 \(y\)原来是 \(x\)的那个儿子
代码如下
void push_up(int x){
tr[x].son=tr[tr[x].ch[0]].son+tr[tr[x].ch[1]].son+tr[x].cnt;
//当前节点儿子数量等于左儿子数量加右儿子数量加当前节点数量
}
void xuanzh(int x){
int y=tr[x].fa;
int z=tr[y].fa;
int k=(tr[y].ch[1]==x);
//判断x是否是y的右儿子
tr[z].ch[tr[z].ch[1]==y]=x;
tr[x].fa=z;//x变到原来y的位置
tr[y].ch[k]=tr[x].ch[k^1];
tr[tr[x].ch[k^1]].fa=y;
//x的原来在x在y的相对位置的那个儿子变成了y原来是x的那个儿子
tr[x].ch[k^1]=y;
tr[y].fa=x;
//y变成了x原来在y的相对的那个儿子
push_up(y);
push_up(x);
//更新节点信息
}
3、将一个节点上旋至规定点
我们是不是对于某一个节点连续进行两次旋转操作就可以呢
一般情况下是可以的,但是如果遇到下面的情况就不可行了
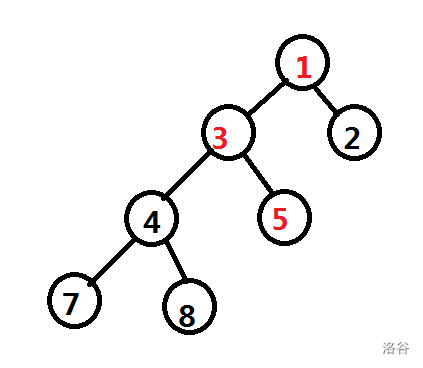
我们要把\(4\)旋转到\(1\)的位置
如果我们一直将\(4\)进行旋转操作,那么旋转两次后的图变成了下面这样

我们会发现\(1-3-5\)这一条链仍然存在
只不过是\(4\)号节点跑到了原来\(1\)号节点的位置
这样的话,\(Spaly\)就失去了意义
因此,我们分情况讨论:
(\(x\)是\(y\)的儿子节点,\(y\)是\(z\)的儿子节点,将\(x\)旋转到\(z\))
1、\(x\)和\(y\)分别是\(y\)和\(z\)的同一个儿子
先旋转\(y\)再旋转\(x\)
2、\(x\)和\(y\)分别是\(y\)和\(z\)不同的儿子
将\(x\)旋转两次
代码
void splay(int x,int goal){
//将x旋转至目标节点goal的儿子
while(tr[x].fa!=goal){
int y=tr[x].fa;
int z=tr[y].fa;
if(z!=goal){
(tr[y].ch[0]==x)^(tr[z].ch[0]==y)?xuanzh(x):xuanzh(y);
}
//分情况讨论:同位置儿子旋转y,不同位置儿子旋转x
xuanzh(x);
//最后旋转x
}
if(goal==0) rt=x;
//如果旋转到根节点,将根节点更新为x
}
4、查找操作
类似于二分查找
从根节点开始,如果要查询的值大于该点的值,向右儿子递归
否则向左儿子递归
如果当前位置的值已经是要查找的数,则将该节点旋转至根节点
所以答案就是此时根的左儿子的儿子数,注意如果根节点的值小于x,要加上根节点的数量
void zhao(int x){
//查找x的位置,并将其旋转至根节点
int u=rt;
if(!u) return;//树为空
while(tr[u].ch[x>tr[u].val] && x!=tr[u].val){
//当存在儿子并且当前位置的值不等于x
u=tr[u].ch[x>tr[u].val];//跳转到儿子
}
splay(u,0);
//将当前位置旋转到根节点
}
5、插入操作
和查找操作类似,也是从根节点开始
如果要插入的值大于该点的值,向右儿子递归
否则向左儿子递归
如果可以在原树中找到当前值,把节点的数量加一即可
否则再新建一个节点
void ad(int x){
//插入价值为x的节点
int u=rt,fa=0;
while(u && tr[u].val!=x){
fa=u;
u=tr[u].ch[x>tr[u].val];
//向儿子递归
}
if(u) tr[u].cnt++;
//如果当前节点已经存在,节点的个数加一
else {
//如果不存在,建立一个新的节点
u=++tot;
if(fa) tr[fa].ch[x>tr[fa].val]=u;
tr[tot].ch[1]=0;
tr[tot].ch[0]=0;
tr[tot].val=x;
tr[tot].fa=fa;
tr[tot].cnt=1;
tr[tot].son=1;
}
splay(u,0);//将当前节点上旋至根节点
}
6、查询前驱和后继
我们要查询某一个数\(x\)的前驱和后缀
首先我们要使用查找操作,将\(x\)节点旋转到根节点
如果查询前驱,那么前驱就是左子树中权值最大的节点
那我们就从左子树开始,一直向右子树跳,直到没有右子树为止
查询后继也是同样
int qq_hj(int x,int jud){
//jud为0查询前驱,为1查询后缀
zhao(x);
//将x旋转至根节点
int u=rt;
if((tr[u].val>x && jud) || (tr[u].val<x && !jud)){
return u;
}
//如果无法继续向下跳,返回当前节点
u=tr[u].ch[jud];
while(tr[u].ch[jud^1]){
u=tr[u].ch[jud^1];
}
//否则继续向下跳
return u;
}
7、删除操作
如果我们要删除某一个数\(x\)
那么这一个数的权值一定介于它的前驱和它的后继之间
所以我们可以先把它的前驱旋转至根节点
然后把它的后继旋转到它的前驱作为前驱的右儿子
这时,前驱的左儿子恰好比前驱大、后继小,正是我们想要删除的值
void sc(int x){
int qq=qq_hj(x,0);
//求出前驱
int hj=qq_hj(x,1);
//求出后继
splay(qq,0);
//将前驱旋转至根节点
splay(hj,qq);
//将后继旋转至前驱的右儿子
int willsc=tr[hj].ch[0];
//找出要删除的数
if(tr[willsc].cnt>1){
tr[willsc].cnt--;
splay(willsc,0);
} else {
tr[hj].ch[0]=0;
}
//删除该节点
}
8、查找第k小的值
从根节点开始,如果左子树的儿子数大于\(k\),向左子树查询
否则向右子树查询
递归解决问题即可
int kth(int x){
int u=rt;
if(tr[u].son<x) return 0;
//如果树的节点数小于x,查找失败
while(1){
int y=tr[u].ch[0];
if(x>tr[y].son+tr[u].cnt){
x-=(tr[y].son+tr[u].cnt);
u=tr[u].ch[1];
//向右子树查询
} else {
if(x<=tr[y].son) u=y;
else return tr[u].val;
//向左子树查询
}
}
}
练习题(洛谷P3369)
一道很基础的板子题,直接附上代码
#include<cstdio>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
const int INF=0x3f3f3f3f;
struct trr{
int son,ch[2],fa,cnt,val;
}tr[maxn];
int n,rt,tot;
void push_up(rg int da){
tr[da].son=tr[tr[da].ch[0]].son+tr[tr[da].ch[1]].son+tr[da].cnt;
}
void xuanzh(rg int x){
rg int y=tr[x].fa;
rg int z=tr[y].fa;
rg int k=(tr[y].ch[1]==x);
tr[z].ch[tr[z].ch[1]==y]=x;
tr[x].fa=z;
tr[y].ch[k]=tr[x].ch[k^1];
tr[tr[x].ch[k^1]].fa=y;
tr[x].ch[k^1]=y;
tr[y].fa=x;
push_up(y);
push_up(x);
}
void splay(rg int x,rg int goal){
while(tr[x].fa!=goal){
rg int y=tr[x].fa;
rg int z=tr[y].fa;
if(z!=goal){
(tr[y].ch[0]==x)^(tr[z].ch[0]==y)?xuanzh(x):xuanzh(y);
}
xuanzh(x);
}
if(goal==0) rt=x;
}
void zhao(rg int x){
rg int now=rt;
if(!now) return;
while(tr[now].ch[x>tr[now].val] && x!=tr[now].val){
now=tr[now].ch[x>tr[now].val];
}
splay(now,0);
}
void ad(rg int x){
rg int now=rt,fa=0;
while(now && tr[now].val!=x){
fa=now;
now=tr[now].ch[x>tr[now].val];
}
if(now) tr[now].cnt++;
else {
now=++tot;
if(fa) tr[fa].ch[x>tr[fa].val]=now;
tr[tot].ch[1]=tr[tot].ch[0]=0;
tr[tot].val=x;
tr[tot].fa=fa;
tr[tot].cnt=1;
tr[tot].son=1;
}
splay(now,0);
}
int qq_hj(rg int x,rg int jud){
zhao(x);
rg int now=rt;
if((tr[now].val>x && jud) || (tr[now].val<x && !jud)){
return now;
}
now=tr[now].ch[jud];
while(tr[now].ch[jud^1]) now=tr[now].ch[jud^1];
return now;
}
void sc(rg int x){
rg int qq=qq_hj(x,0),hj=qq_hj(x,1);
splay(qq,0);
splay(hj,qq);
rg int now=tr[hj].ch[0];
if(tr[now].cnt>1){
tr[now].cnt--;
splay(now,0);
} else {
tr[hj].ch[0]=0;
}
}
int kth(rg int k){
rg int now=rt;
if(tr[now].son<k) return 0;
while(1){
rg int y=tr[now].ch[0];
if(k>tr[y].son+tr[now].cnt){
k-=(tr[y].son+tr[now].cnt);
now=tr[now].ch[1];
} else {
if(k<=tr[y].son) now=y;
else return tr[now].val;
}
}
}
int main(){
n=read();
ad(INF);
ad(-INF);
rg int aa,bb,ans;
for(int i=1;i<=n;i++){
aa=read(),bb=read();
if(aa==1) ad(bb);
else if(aa==2) sc(bb);
else if(aa==3) {
zhao(bb);
ans=tr[tr[rt].ch[0]].son+(tr[rt].val<bb?tr[rt].cnt:0);
printf("%d\n",ans);
} else if(aa==4){
ans=kth(bb+1);
printf("%d\n",ans);
} else if(aa==5){
ans=qq_hj(bb,0);
printf("%d\n",tr[ans].val);
} else {
ans=qq_hj(bb,1);
printf("%d\n",tr[ans].val);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号