【算法】BFS、并查集和拓扑排序

最近刷到了两道关于图论很有意思的题目（）。做法颇有相似之处，因此记录一下吧

AcWing2069. 网络分析

标签:dfs、并查集

题目描述

题目大意是，有一个\(n\)个顶点的网络，初始状态图中没有边。
有两种操作：操作1将节点\(a\)和节点\(b\)连接起来；操作2使节点\(p\)的值加\(t\)，\(t\)值会沿着网络传送到每一个相邻的节点及其所有子节点。
最后要输出一系列操作后所有节点的值。
因此考虑使用并查集维护图中所有的联通块，便于维护每个块的规模和块的值。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110010;

int n, m;
int p[N], d[N];

int find(int x)
{
    if (p[x] != x)
    {
        if (p[p[x]] == p[x]) return p[x];
        int r = find(p[x]);
        d[x] += d[p[x]];
        p[x] = r;
    }
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < N; i ++ ) p[i] = i;

    int k = n;
    while (m -- )
    {
        int t, a, b;
        scanf("%d%d%d", &t, &a, &b);
        if (t == 1)
        {
            a = find(a), b = find(b);
            if (a != b)
            {
                k ++ ;
                p[a] = p[b] = k;
            }
        }
        else
        {
            a = find(a);
            d[a] += b;
        }
    }

    for (int i = 1; i <= n; i ++ )
        if (i == find(i)) printf("%d ", d[i]);
        else printf("%d ", d[i] + d[find(i)]);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/603227/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

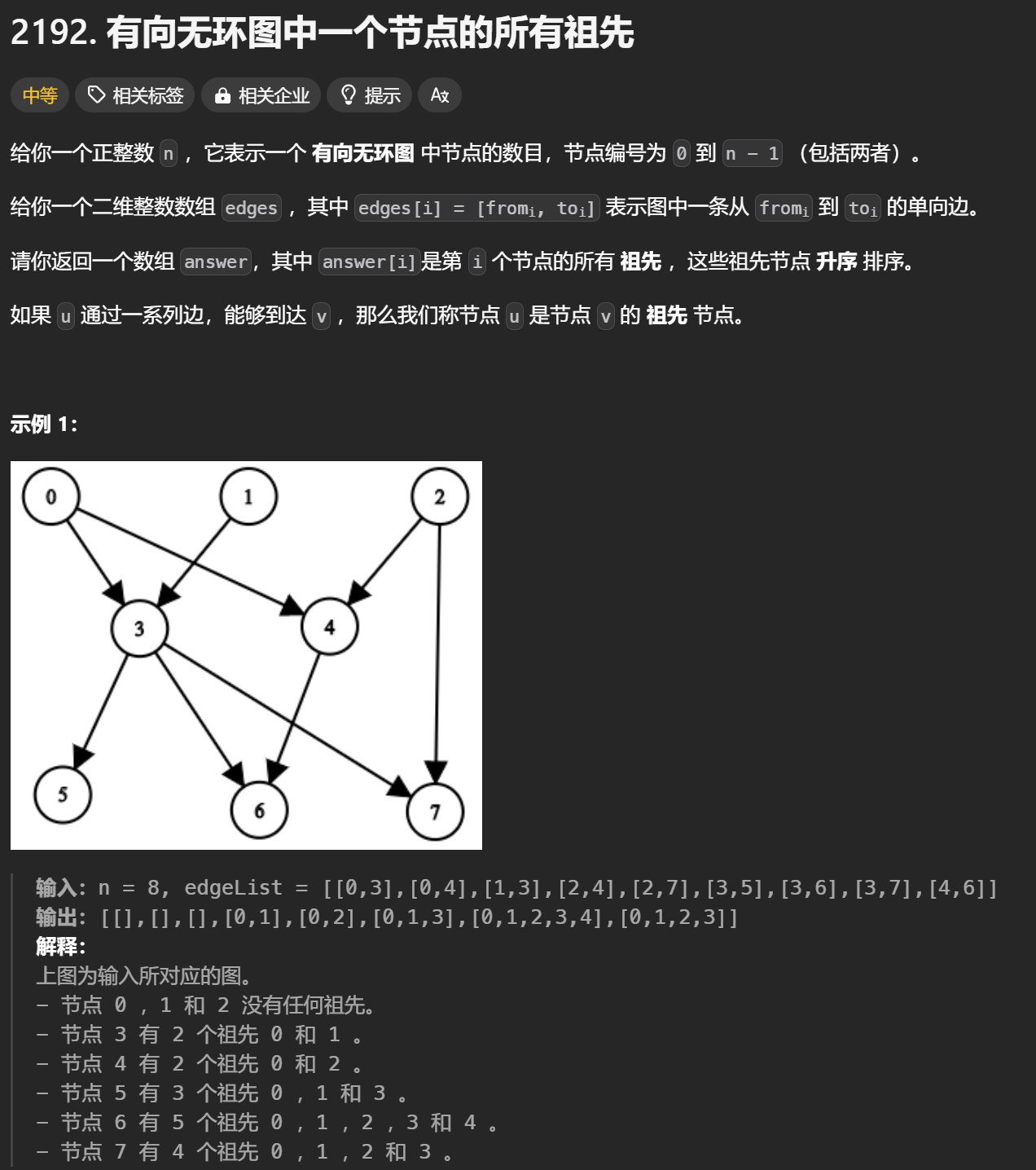
LC2192. 有向无环图中一个节点的所有祖先

class Solution {
public:
    vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
        vector<unordered_set<int>> anc(n);//每个结点的祖先数组
        vector<vector<int>> e(n);//邻接表
        vector<int> indeg(n);//入度表
        //预处理邻接表和入度表
        for (const auto &edge: edges)
        {
            e[edge[0]].push_back(edge[1]);//[from, to]
            ++indeg[edge[1]];
        }
        //bfs实现拓扑排序
        queue<int> q;
        for (int i=0;i<n;i++)//每个顶点
        {
            if (!indeg[i]) q.push(i);
        }
        while (!q.empty())
        {
            int u=q.front();
            q.pop();
            for (int v:e[u])
            {
                anc[v].insert(u);
                for (int i:anc[u]) anc[v].insert(i);
                --indeg[v];
                if (!indeg[v]) q.push(v);
            }
        }
        vector<vector<int>> res(n);
        for (int i=0;i<n;i++)
        {
            for (int j:anc[i]) res[i].push_back(j);
            sort(res[i].begin(), res[i].end());
        }
        return res;
    }
};

第一题是并查集+树上搜索的结合体,第二题是BFS+图的基操+拓扑排序