机器学习公开课备忘录（三）支持向量机SVM

机器学习公开课备忘录（三）支持向量机SVM

对应机器学习公开课第七周，但是由于Andrew Ng为了课程更加通俗化，对SVM背后的原理并没有太多涉及，最近在看周志华老师的《机器学习》，希望日后能补上对SVM更详细的解释。

SVM

在logistic回归中，
对于\(y=1，希望有h_\theta(x) \approx 1，则 \theta^Tx \gg 0;\)
对于\(y=0，希望有h_\theta(x) \approx 0，则 \theta^Tx \ll 0;\)
为此，定义下面新的代价函数\(cost_1和cost_0\)：


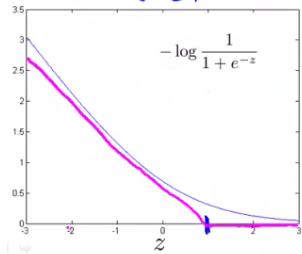
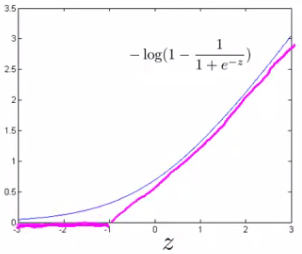
logistic的代价函数为：

\[\min\limits_\theta \frac{1}{m}\left[\sum\limits_{i=1}^{m}y^{(i)}(-\log(h_\theta(x^{(i)}))) + (1-y^{(i)})(-\log(1-h_\theta(x^{(i)})))\right] + \frac{\lambda}{2m}\sum\limits_{j=1}^{n}\theta_{j}^2 \]

将其修改为\(CA+B\)的形式，并对代价函数做修改，得到：

\[\min\limits_\theta C\left[\sum\limits_{i=1}^{m}y^{(i)}cost_1(\theta^Tx^{(i)}) + (1-y^{(i)})cost_0(\theta^Tx^{(i)})\right] + \frac{1}{2}\sum\limits_{j=1}^{n}\theta_{j}^2 \]

想要代价函数取得最小，必须有\(A \approx 0\)，而这决定了每个样本的代价函数都必须为零，因此此时的SVM问题转化成：

\[\begin{align*}&\min\limits_\theta\frac{1}{2}\sum\limits_{j=1}^{n}\theta_j^{2}\\ &s.t.\quad\begin{cases}\theta^{T}x^{(i)}\geq 1 \quad y^{(i)}=1\\\theta^{T}x^{(i)}\leq -1 \quad y^{(i)}=0\end{cases}\end{align*} \]

考虑将\(y=0\)的负类用\(y=1\)代替，则上式可以写作：

\[\min_\theta\frac{1}{2}\sum_{j=1}^n\theta_j^2 \\ s.t.　y^{(i)}(\theta^Tx^{(i)}+b) \ge 1 \]

这也是SVM的基本型

最大间隔

（原课程使用了向量投影的解释，这里直线的距离解释参考了周志华老师的《机器学习》一书）
SVM的效果是在划分数据上实现最大间距分类，即large margin classfier，例如下图这种情况应用SVM就会得到黑色实线

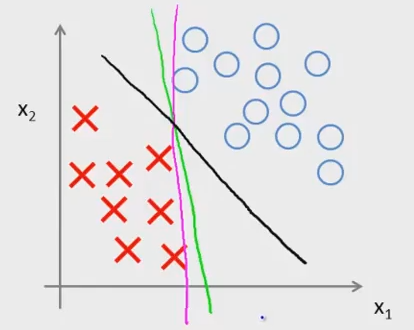
这是因为，\(x到超平面或直线的距离r = \frac{|\theta^Tx^{(i)}|}{||\theta||}\)，而对于离直线最近的点，因为刚好是在边界上，分母为1和-1，它们之间的距离为 \(r = \frac{2}{||\theta||}\)，若求\(\theta\)的最小值，即是分母最小，则间距最大

Kernel核函数

该部分应该是SVM最复杂的部分，但是本课程并没有涉及到核函数是如何引入，如何解决低维到高维映射时的计算问题的，因此这里也只针对课程内容做一些简单叙述
对于某些不可线性划分的特征，构造非线性边界，一种方法是使用多项式，另一种就是使用核函数
对于原有的某个数据点\(x\)，和空间中另一点\(l^{(i)}\)的相似度定义为：

\[f_i=similarity(x, l^{(i)})=exp\left(-\frac{||x-l^{(i)}||^2}{2\sigma^2}\right) \]

当选用\(k\)个数据点的时候，就可以构造k个新特征

SVM的使用

1. 标记点选择：所有样本都作为特征点，构造新的特征f
2. 假设：若 \(\theta^Tf \ge 0\)，预测\(y=1，否则y=0\)
3. C的选择：C的选择(\(\approx \frac{1}{\lambda}\))，C过大，易造成低偏差、高方差；C过小，会造成高偏差，低方差
4. 核函数参数选择：\(\sigma\)过大，会造成高偏差，低方差；过小则会造成高方差，低偏差
5. SVM在解决多分类问题时采取和Logistic回归同样的思路
6. SVM的时间消耗很大，当m过大时，不宜采用SVM，适合用逻辑回归；当m不是很大时，视n选择逻辑回归与SVM，n相对与m过大则选用逻辑回归，过小则选用SVM
7. Kernel不止高斯核一种，当使用kernel后，也需要对新特征做feature scaling