AcWing 1014. 登山

$AcWing$ $1014$. 登山

一、题目描述

五一到了，$ACM$队组织大家去登山观光，队员们发现山上一共有$N$个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号。

同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。

队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？

输入格式
第一行包含整数$N$，表示景点数量。

第二行包含$N$个整数，表示每个景点的海拔。

输出格式
输出一个整数，表示最多能浏览的景点数。

数据范围
$2≤N≤1000$

输入样例：

8
186 186 150 200 160 130 197 220

输出样例：

4

二、题意分析

三、题目总结

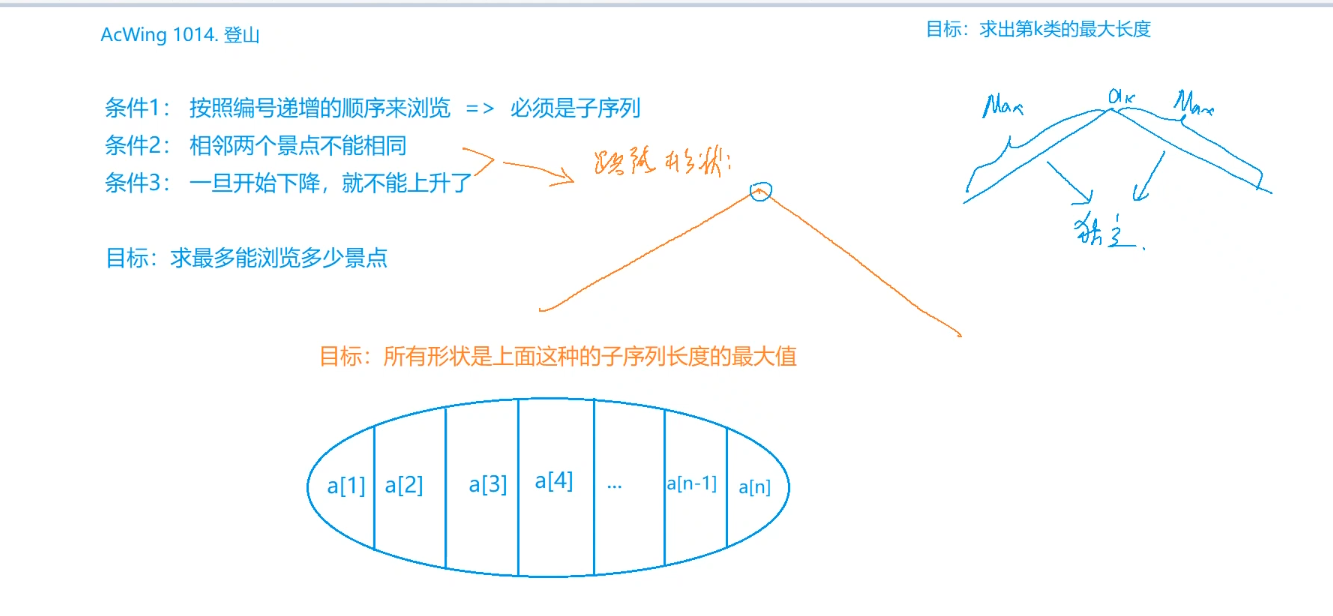
• 按照编号递增的顺序来浏览

• 相邻两个景点不能相同

• 一旦开始下降，就不能上升了

目标：求最多能浏览多少景点

必须是先严格单调上升，再严格单调下降！

坑点：假如某个景点是最高点，从左数是$n$,从右数是$m$,那么以此景点为最高点时整个所有景点的长度就是$n+m-1$个。

四、朴素版本$O(N^2)$

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;
int n;    // 山的个数
int a[N]; // 山的高度数组
int f[N]; // 最长上升子序列
int g[N]; // 最长下降子序列
int res;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    // 正向
    for (int i = 1; i <= n; i++) {
        f[i] = 1;
        for (int j = 1; j < i; j++)
            if (a[i] > a[j]) f[i] = max(f[i], f[j] + 1);
    }
    // 反向
    for (int i = n; i >= 1; i--) {
        g[i] = 1;
        for (int j = n; j > i; j--)
            if (a[i] > a[j]) g[i] = max(g[i], g[j] + 1);
    }

    // 每个点，都可能是两者相加的最大位置处，所以，需要枚举每个点，每个点都有资格参评最优点
    // 因为最终的那个中间点，左边计算了一次，右边又计算了一次，需要减1去重复
    for (int i = 1; i <= n; i++) res = max(res, f[i] + g[i] - 1);
    // 输出
    printf("%d\n", res);
    return 0;
}

五、贪心+二分优化版本$(O(NlogN))$

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int n, a[N];

// f[i]:长度为i的正序递增序列中，末尾元素最小的是f[i]
// p1[i]:记录第i个数字被放的f数组中位置,也就是正序排名第几
int f[N], fl, p1[N];

// g[i]:长度为i的倒序递增序列中，末尾元素最小的是g[i]
// p2[i]:记录第i个数字被放的g数组中位置,也就是倒序排名第几
int g[N], gl, p2[N];

int res;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    // 正向
    f[++fl] = a[1];
    p1[1] = 1;

    for (int i = 2; i <= n; i++)
        if (a[i] > f[fl]) {
            f[++fl] = a[i];
            p1[i] = fl;
        } else {
            int t = lower_bound(f + 1, f + fl + 1, a[i]) - f;
            f[t] = a[i];
            p1[i] = t;
        }

    // 反向
    g[++gl] = a[n];
    p2[n] = 1;

    for (int i = n - 1; i >= 1; i--)
        if (a[i] > g[gl]) {
            g[++gl] = a[i];
            p2[i] = gl;
        } else {
            int t = lower_bound(g + 1, g + gl + 1, a[i]) - g;
            g[t] = a[i];
            p2[i] = t;
        }

    for (int i = 1; i <= n; i++) res = max(res, p2[i] + p1[i] - 1);

    printf("%d\n", res);
    return 0;
}

六、状态机分析法

这是我做过 $AcWing$第二场热身赛的$C$题——$AcWing$ $3549$. 最长非递减子序列 后总结出来的一类模型

那就是，利用状态机模型$DP$解决最长$xxx$子序列模型 的方法

$xxx$可以是先上升后下降，或者先上升后下降再上升，或者先上升后下降再上升再下降 ···

回到本题，我们就可以先利用 状态机模型 进行分析，具体如下：

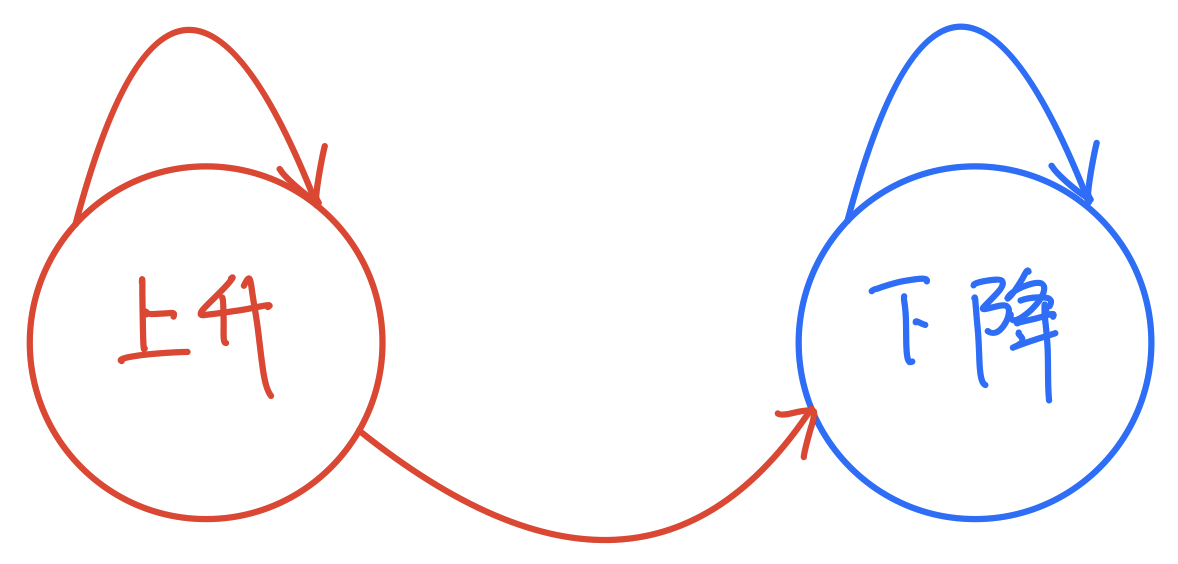
对于本题来说，当前 状态 如果是 上升状态，则它下一个阶段可以 维持上升状态，或者变成 下降状态

而对于已经处于 下降状态 来说的 状态，下一个阶段只能继续 维持下降状态

于是便可以写出 状态机模型的闫氏$DP$分析法：

闫氏$DP$分析法

$\large \left\{\begin{aligned} 状态表示f_{i,j} & \left\{\begin{aligned} 集合：以第i个位置作为当前子序列的右端点，且当前状态为j& \\ 属性：方案的子序列长度最大Max& \end{aligned}\right. \\ 状态转移 & \left\{\begin{aligned} f_{i,0}=max\{\sum f_{k,0}\}+1& \\ f_{i,1}=max\{\sum f_{k,0},\sum f_{k,1}\}+1 & \end{aligned}\right. \\ \end{aligned}\right.$

注：$0$：上升,$1$：下降

初始化: $f[i][0]=f[i][1]=1$

目标状态: 枚举 $max(f[i][0],f[i][1])$

大家想更近一步了解这类模型的话，可以做一下这道题 $AcWing$ $3549$. 最长非递减子序列

$Code$

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int n;
int a[N];
int f[N][2];

int main() {
    // input
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    // dp
    for (int i = 1; i <= n; i++) {
        f[i][0] = f[i][1] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) f[i][0] = max(f[i][0], f[j][0] + 1);
            if (a[j] > a[i]) f[i][1] = max(f[i][1], max(f[j][0], f[j][1]) + 1);
        }
    }

    // find result from all final states
    int res = 0;
    for (int i = 1; i <= n; i++) res = max(res, max(f[i][0], f[i][1]));
    cout << res << endl;
    return 0;
}