编程学习笔记(LeetCode-977. 有序数组的平方)

编程学习笔记(LeetCode-977. 有序数组的平方)

<977> 有序数组的平方

• 问题重述：
  给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

• 例如：

示例 1：

输入： nums = [-4,-1,0,3,10]
输出： [0,1,9,16,100]
解释： 平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入： nums = [-7,-3,2,3,11]
输出： [4,9,9,49,121]

限定：

• \(1 \leqslant nums.length \leqslant 10^4\)
• \(-10^4 \leqslant nums[i] \leqslant 10^4\)
• \(nums\) 已按 非递减顺序 排序

问题分析与求解：

最简单直接的方法就是将数组 \(nums\) 中的元素平方后，再排序：

C++实现如下：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        for(int i=0; i<nums.size(); i++){
            nums[i] = nums[i]*nums[i];
        }
        sort(nums.begin(), nums.end());
        return nums;
    }
};

由于给出的数组是有一定规律的，直接平方然后排序的方法固然简单，运行效率貌似也不错，但是我们尚且可以再提高一下运行效率。

那就是采用双指针的方法：

图1.977.1 双指针

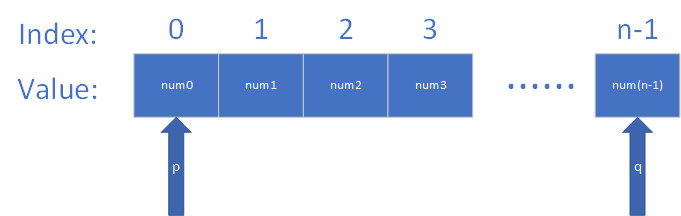
• 首先，我们要新建两个指针 \(p\) 和 \(q\) 让它们分别指向问题给出的数组 \(num\) 的首尾位置，\(p\) 和 \(q\) 都是不断的向数组中间方向迭代的，当 \(p < q\) 的时候说明迭代结束。
• 再新建一个用于存储结果数组 \(res\)
• 然后通过比较 \(p\) 和 \(q\) 分别指向元素的平方大小，比较大的就插入到结果数组 \(res\) 前面，平方数相等的话就同时插入。
• 让 \(p\) 或 \(q\) 指向下一个元素（当 \(p\) 和 \(q\) 指向的元素的平方数相等时，\(p\) 和 \(q\) 同时分别指向下一元素）

C++代码实现如下：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        //存储结果的返回数组
        vector<int> res;
        //双指针，分别指向给定数组的首尾
        int p, q;
        p=0;
        q=nums.size()-1;
        //当p<q的时候说明已经已经全部迭代完了
        while(p < q){
            int t1 = nums[p]*nums[p];
            int t2 = nums[q]*nums[q];
            //t1>t2说明p指向的元素平方后比q的大
            if(t1>t2){
                res.insert(res.begin(), t1);
                p++;
            }
            //t1<t2说明p指向的元素平方后比q的小
            else if(t1<t2){
                res.insert(res.begin(), t2);
                q--;
            }
            //t1==t2说明p指向的元素平方后和q的一样
            else{
                res.insert(res.begin(), t1);
                res.insert(res.begin(), t2);
                p++;
                q--;
            }
        }
        //如果跳出循环后，发现双指针指向同一个元素，说明还有一个元素没有插入
        if(p==q){res.insert(res.begin(), nums[p]*nums[p]);}
        return res;
    }
};

怎么回事？不是说好的提升效率吗？怎么反而时间效率更低了？

经过查询后，发现原来问题出现在vector容器：

• vector容器的底层实际上是一段连续的内存空间，并且起始地址是不变的，所以它能非常好的支持随机存取。但是当我们在中间进行插入和删除操作时，会造成内存块的拷贝，另外，当该数组的内存空间不够时，需要重新申请一块足够大的内存并进行内存拷贝，这些都大大的影响了vector的效率。
• 同时，在vector容器中，对头部和中间的元素进行插入删除需要移动内存，如果元素是结构体或者类，那么移动时还会进行析构和构造操作，所以性能不高
• 所以vector容器对末尾的元素的操作最快，此时一般不需要移动内存，只有剩余内存不够时才需要。

vector容器一些操作的时间复杂度：

• 头部插入删除：\(O(N)\)
• 尾部插入删除：\(O(1)\)
• 中间插入删除：\(O(N)\)
• 查找：\(O(N)\)

所以，我们使用双指针实现的程序，不仅效率没有提高，反而更低了，所以进行了如下改进：

• 增加一个 \(cur\) 指针，让它指向返回结果数组 \(res\) 的末尾（问题给定数组的大小是已知的，所以返回数组大小也可以确定）。
• 当 \(p\) 和 \(q\) 指针比较两个元素后，就把符合条件的数值存储在 \(res\) 中索引为 \(cur\) 位置上，然后移动 \(cur\) 指针。

那么修改后的C++代码如下：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> res(nums.size());
        int p, q, cur;
        cur=nums.size()-1;      //指向返回数组的末尾
        p=0;
        q=nums.size()-1;
        while(p < q){
            int t1 = nums[p]*nums[p];
            int t2 = nums[q]*nums[q];
            if(t1>t2){
                res[cur] = t1;
                cur--;
                p++;
            }
            else if(t1<t2){
                res[cur] = t2;
                cur--;
                q--;
            }
            else{
                res[cur] = t1;
                cur--;
                res[cur] = t2;
                cur--;
                p++;
                q--;
            }
        }
        if(p==q){res[cur] = nums[p]*nums[p];}
        return res;
    }
};

总结：

• 采用直接平方再排序的方法，程序的时间复杂度取决于排序算法的选取，此处采用了标准库的排序函数，时间复杂度为 \(O(nlogn)\) ，其中 \(n\) 是数组 \(nums\) 的长度；此处用时为\(36ms\)。
• 采用双指针的方法，并且采用在vector容器的begin位置插入的方式，那么运行效率不仅没有提高，反而降低了不少。此处用时为 \(1328ms\)。
• 如果采用双指针的方法，并且采用在vector容器的end位置向begin方向迭代方式，那么效率便会提高。时间复杂度为 \(O(n)\) ，其中 \(n\) 是数组 \(nums\) 的长度。此处用时为 \(24ms\)。比直接排序的方法快了一点。
• 使用vector容器的时候要注意在各个位置插入元素的时间复杂度。