AT/CF 记录

AT ARC197

赛时只想了 \(B, C, D\)，但是 \(A\) 也是简单题就不写了。

B - Greater Than Average

• 标签： 贪心

• 难度： 下位绿

• 赛时： 思考 \(< 1min\)，代码 \(< 10min\)

首先对 \(a\) 排序，容易发现若选择集合 \(S\) 不是一个 \(a\) 中的区间，那么把扣掉的点加入一定是不劣的。证明：设 \(S\) 的平均值为 \(x\)，那么选择 \(< x\) 的数显然变优，若选择 \(> x\) 的数这个数一定是大于新的最小值，所以答案要么 \(+1\)，要么不变。进一步的，可以发现答案一定来自 \(a\) 中的一个前缀。双指针 \(O(n)\) 即可。

C - Removal of Multiples

• 标签： 简单 \(\rm DS\)

• 难度： 上位绿 ~ 下位蓝

• 赛时： 思考 \(20min\)，代码 \(? min\)

注意到答案不会太大，所以考虑关于答案大小的做法。然后发现若去重 \(b\) 之后枚举量就是调和级数，使用 \(\rm BIT\) 上二分维护即可，时间复杂度 \(O(V \log n + V \log V)\)。

D - Ancestor Relation

• 标签： 计数，结构刻画

• 难度： 下位紫 ~ 上位蓝

• 赛时： 思考 \(40min\)，代码赛后补了。

首先把 \(a\) 作为邻接矩阵建出图 \(G\)，考虑如何在 \(G\) 上刻画树 \(T\) 的形态。注意到点集 \(S\) 在 \(T\) 上若是一条直上直下的链，那么 \(G\) 上 \(S\) 应该构成一个团。进一步的，考察下面分叉在 \(G\) 上的形态。

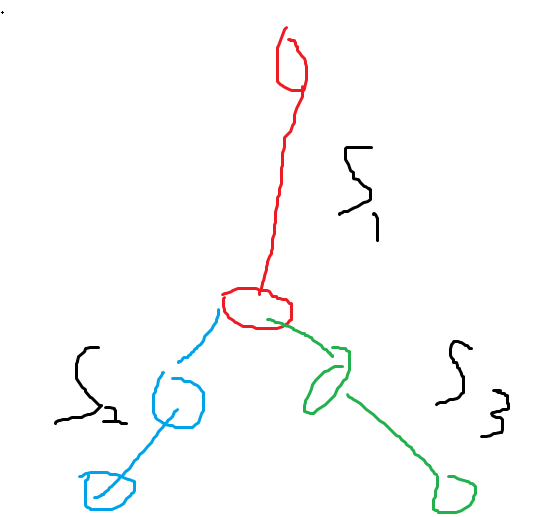
在 \(G\) 上，\(S_1, S_2, S_3, S_1 \cup S_2, S_1 \cup S_3\) 应该都是完全图，而且 \(S_2\) 与 \(S_3\) 应该互相没有任何连边，即 \(S_1\) 与 \(S_2\) 两者独立，一般化的，对于有多个分叉的情况也是适用的。考虑一个点 \(u\) 是否可以在 \(S_1\) 中，那么相当于 \(u\) 是否可以到达当前子图的所有点。每次把 \(S_1\) 从图中删去，则问题递归为若干个子图，且子图的结构与原图相同，即划分成若干个子问题。

具体的，考虑原图中的某个连通块 \(G\)，找到 \(G\) 中可以到达 \(G\) 中所有点的点集 \(S\)，根据分析这个点集就是上述的 \(S_1\)，若 \(S_1\) 为空，则给出的 \(G\) 不合法。不难发现 \(S_1\) 中的点可以任意重排，于是方案数为 \(|S_1|!\)。然后把 \(S_1\) 删去，递归为若干个互不相交的子问题。注意，由于 \(1\) 必须是根，所以 \(1\) 所在的 \(S\) 所代表的链的头部已经确定，要少乘个 \(|S|\)。

代码实现上，可以每次只删去 \(S\) 中的一个点，并乘上当前 \(S\) 的大小。时间复杂度 \(O(n^3)\)，比较好写。

qwq

#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;

const int N = 400 + 10, M = 2e5 + 10;
const ll mod = 998244353;

il ll qpow(ll& x, ll y){
  ll ret = 1;
  for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
  return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
//#define int long long

int n, a[N][N], del[N], deg[N], vis[N], ndc;

void dfs(int u){
  //cerr << "DDD:" << u << "\n";
  vis[u] = 1; ndc++;
  for(int i = 1; i <= n; i++){
    if((!del[i]) && a[u][i]){
      //cerr << i << " " << u << "\n";
      deg[i]++; deg[u]++;
      if(!vis[i]) dfs(i);
    }
  }
}

void solve(){
  cin >> n;
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= n; j++)
      cin >> a[i][j];
  int cnt = 0; ll ans = 1;
  while(cnt < n){
    int p = 1;
    for(; p <= n; p++) if(!del[p]) break;
    for(int i = 1; i <= n; i++) vis[i] = deg[i] = 0; ndc = 0;
    dfs(p); ll res = 0, delp = 0;
    for(int i = 1; i <= n; i++){
      if(vis[i] && deg[i] == ndc * 2){
        res++;
        if(!delp) delp = i;
      }
    }
    if(((!cnt) && delp != 1) || delp == 0){cout << 0 << "\n"; return;}
    if(delp != 1) MUL(ans, res);
    else if(deg[1] != n * 2){cout << 0 << "\n"; return;}
    /*cerr << p << " " << res << " " << deg[p] << " " << ndc << "\n";*/ del[delp] = 1; cnt++;
  } cout << ans << "\n";
}

void clr(){
  for(int i = 1; i <= n; i++) del[i] = 0;
}

signed main(){
  ios::sync_with_stdio(0);
  cin.tie(0); cout.tie(0);
  int T; cin >> T; while(T--) solve(), clr();

  return 0;
}

AT ARC202

口胡的。

A - Merge and Increment

从小到大贪心，每次将一个连续段向两侧合并，使用 \(\rm set\) 维护一下即可。

C - Repunits

首先有 \(R_i = \frac{10^{i + 1} - 1}{9}\)，通过观察可以得到 \((R_i, R_j) = (10^{i - j} R_{i - j}, R_j) = (R_{i - j}, R_j)\)。通过辗转相除法可以得到 \((R_i, R_j) = R_{(i, j)}\)。从而有 \(\gcd_{i \in S} R_{a_i} = R_{\gcd_{i \in S} a_i}\)。那么考虑如何把 \(\gcd\) 转成 \(\operatorname{LCM}\)，那么考虑 \(\operatorname{LCM}_{i = 1}^n a_i = \prod_{S \in \{1, 2, ..., n\}} (\gcd_{i \in S} a_i)^{(-1)^{|S| + 1}}\)。那么此时可以每次加入新数然后暴力枚举因数做到 \(O(n\sqrt n)\)。但是我们有一个更加技巧性的做法。即考虑令 \(R_i = \prod_{d | i} F_d\)，我们可以通过筛法在 \(O(n \log n)\) 的时间求出所有的 \(F_n\)。然后通过上面的结论，不难得到 \(\operatorname{LCM}\{S\} = \prod_{d, \exists a \in S, d | a} F_d\)。那么这样就可以做到 \(O(n \log n)\) 了。