图论进阶
Dilworth 定理
考虑一个偏序集 \(G\)。那么有如下定理:
- \(G\) 的最长反链等于 \(G\) 的最小可重链覆盖
以及对偶形式,
- \(G\) 的最长链等于 \(G\) 的最小可重反链覆盖。
其中 可重 指的是路径可交。
-
Proof: 考虑证明原形式,那么对偶形式也可以推出来。首先欲让可重链覆盖达到最小值,那么假如某一个链没有向两边拓展到(入度或出度为 \(0\) )叶子,那么就可以向两边拓展。那么在方案中任意两条链肯定都会至少有一个点没有偏序关系,但是很难直接说明选出的点 \((u,v)\) 没有偏序关系时,剩下的某个链选出的 \(w\) 与这两个都没有关系。
那么考虑分讨:(令初始选的链为 \(A, B\),加入的链为 \(C\))
-
假设 \(A, B\) 没有相交之处:那么此时 \(C\) 中随便选一个都可以。
-
假设 \(A, B\) 有相交之处:继续分讨:
-
\(A, B\) 的起点(终点)相同,并在某一段进行了分叉(最后汇合不管,没有影响):那么 \(C\) 与 \(A, B\) 的起点(终点) 相同 / 是不需要考虑的,那么直接考虑 \(C\) 与 \(A, B\) 有一段相交的情况即可。显然 \(C\) 不可能覆盖 \(A, B\) 中任意一条的整个链,考虑只覆盖了一段区间的情况(最后汇合不影响)。如下图:
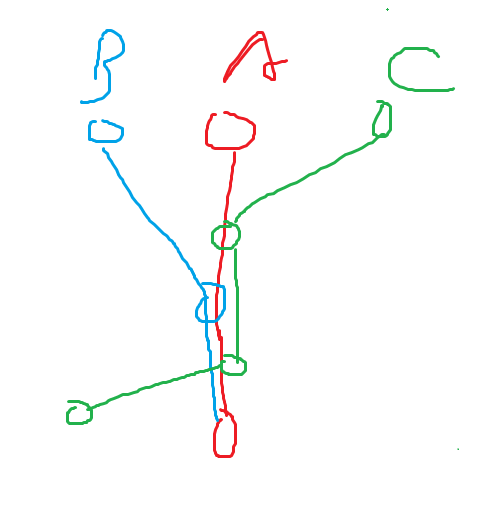
不难发现只要 \(A, B, C\) 都取链头即可满足条件。
但是你注意到并不需要 \(A\) 整条链被覆盖就无解,只需 \(A \to b\)(\(b\) 是蓝点)完全被覆盖即可。所以有这个情况:
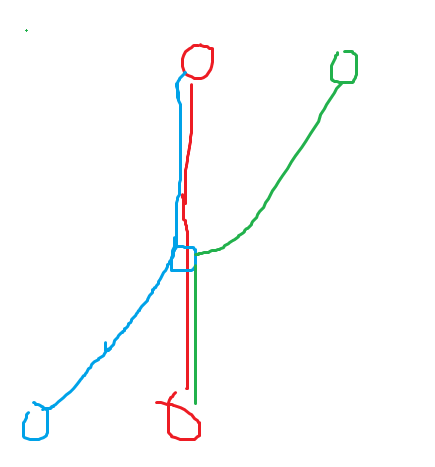
但是这个东西根本不要三条链,两条链就可以覆盖了。所以这个情况不存在啊。
-
\(A, B\) 的起点和终点都不相同,中间只有某段区间是相同的:容易发现此时 \(C\) 不可能接到 \(A\) 的上面,所以 \(A\) 的链顶不可能被覆盖。于是与上面的构造差不多的可以证明出来。然后 \(A\) 下面跟着 \(B\) 的部分也是不可能的,否则可以拓展。
-
于是证明了随便三个链都存在点可以构造出反链。那么再次加入一个链也是可以同理证明的,手玩可以发现这些本质相同。于是就证完了。
-
P4298 CTSC2008 祭祀
首先转化成最小可重链覆盖。那么对原图做传递闭包跑出另一个图,然后这个时候就可以转化成最小路径覆盖了。这个是经典问题,拆点后答案就等于 \(n\) - 二分图匹配。考虑第三问,考虑什么样的点是不可以被选择的,若不可以被选择,说明它选择之后,会使得某两个反链无法选择某个点,即存在某两条选择的反链,这个点在两链分叉处。于是考虑随便选择一个点并且把他的所有相连的点删去,如果答案变小小 \(1\),那么说明这个点是可以选择的,否则不能。感性理解就是删除之后的减小量 \(> 1\),那么说明没有任何一种方案满足它被选择。
那么对于第二问,考虑维护一个选择集合 \(S\),然后每次从第二问所求出来的点中选择一个点,且这个点与 \(S\) 没有关系,然后一直做下去即可。时间复杂度 \(O(n^4)\) - \(O(n^2 \sqrt n)\)。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 100 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
int n, m, con[N][N], kil[N], mat[N], vis[N];
int ans1[N], ans2[N];
bool dfs(int u, int fr){
if(vis[u] == fr) return false;
vis[u] = fr;
for(int v = 1; v <= n; v++){
if(kil[v] || (!con[u][v])) continue;
if(!mat[v] || dfs(mat[v], fr)) return mat[v] = u, true;
} return false;
}
int getans(){
int ret = 0;
for(int i = 1; i <= n; i++) if(!kil[i]) ret -= dfs(i, i) - 1;
return ret;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) con[i][i] = 1;
for(int i = 1; i <= m; i++){
int x, y; cin >> x >> y;
con[x][y] = 1;
}
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++) con[i][j] |= (con[i][k] && con[k][j]);
for(int i = 1; i <= n; i++) con[i][i] = 0;
int ans = getans();
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++) kil[j] = mat[j] = vis[j] = 0;
for(int j = 1; j <= n; j++) if(con[i][j] || con[j][i] || i == j) kil[j] = 1;
int now = getans(); ans2[i] = (ans == now + 1);
}
for(int i = 1; i <= n; i++) kil[i] = 0;
for(int i = 1; i <= n; i++) if(ans2[i] && (!kil[i])){
ans1[i] = 1;
for(int j = 1; j <= n; j++) if(con[i][j] || con[j][i] || i == j) kil[j] = 1;//, cerr << j << "\n";
} cout << ans << "\n";
for(int i = 1; i <= n; i++) cout << ans1[i]; cout << "\n";
for(int i = 1; i <= n; i++) cout << ans2[i]; cout << "\n";
return 0;
}
CF1738G Anti-Increasing Addicts
首先考虑转化,可以把题目所述条件看作一个偏序集,那么相当于要求不存在长度为 \(k\) 的链,根据 \(\rm Dilworth\) 定理,即存在大小为 \(k - 1\) 的最小反链覆盖。那考虑 \(k - 1\) 条链最多可以覆盖多少个点,不难发现,第一条链的长度至多为 \(2n - 1\),第二条至多为 \(2n - 3\),第 \(k - 1\) 条链至多为 \(2n - 2k + 3\)。其实就是除了网格右下角边长为 \(n - k + 1\) 的正方形没有被覆盖。即删除了 \((n - k + 1) ^ 2\) 个格子,恰好满足了题目要求的数量。
那么现在的问题就变成了如何刻画这些链的形态,那么不难发现,这 \(k - 1\) 条链要取满,起点必须在 \((n, i), i \in [1 \dots k - 1]\),且若确定了 \(i\),那么终点也一定得是对应的 \((i, n)\)。前者容易理解,后者是由于若取 \((x, n), x \neq i\),那么一定会存在某一条链的某一个格子与其有交,那么就不能取满了。于是不妨令第 \(i\) 条链是从 \((n, i)\) 到 \((i, n)\),现在就是要使得这 \(k - 1\) 条链完全覆盖所有不能被删除的点(称为关键点)。考虑从 \(k - 1\) 从大到小考虑每条链应该怎么走。若当前在的位置右边还有关键点,那么必须前往,否则会被这条链的轮廓所框住,以后也无法覆盖这个关键点。若右侧没有关键点,那么向上走,这样可以尽量覆盖更多的点。
最后判断是否所有关键点都被覆盖即可,时间复杂度为 \(O(n^2)\)。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
using namespace std;
const int N = 1000 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
//#define int long long
int n, k, cnt[N][N], del[N], chosen[N][N], los[N][N];
void solve(){
cin >> n >> k;
for(int i = 1; i <= n; i++){
string str; cin >> str; str = "*" + str;
for(int j = 1; j <= n; j++) los[i][j] = cnt[i][j] = ((str[j] - '0') ? 0 : 1);//, cerr << los[i][j];
for(int j = n - 1; j; j--) cnt[i][j] += cnt[i][j + 1];
}
for(int i = k - 1; i; i--){
int y = i;
for(int x = n; x >= i; x--){
int dell = 0; chosen[x][y] = 1; dell += los[x][y];
while(cnt[x][y + 1] - del[x] > 0) y++, chosen[x][y] = 1, dell += los[x][y];
//cerr << x << " " << y << " " << cnt[x][y + 1] << "\n";
del[x] += dell;
}
while(y < n) chosen[i][++y] = 1;
}
bool ans = 1;
//for(int i = 1; i <= n; i++) cerr << cnt[i][1] << " " << del[i] << "\n";
for(int i = 1; i <= n; i++) if(cnt[i][1] > del[i]) ans = 0;
if(!ans){cout << "NO" << "\n"; return;}
else{
cout << "YES" << "\n";
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cout << chosen[i][j];
} cout << "\n";
}
}
}
void clr(){
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) chosen[i][j] = cnt[i][j] = del[i] = 0;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int T; cin >> T; while(T--) solve(), clr();
return 0;
}
广义串并联图
定义一个图 \(G\) 为广义串并联图,当且仅当 \(G\) 中不含与 \(\rm K4\) 同胚的子图。即不存在 \(4\) 个节点两两之间有 \(6\) 条不交的路径。那么这样的图可以由以下三种操作变成一个点:
-
删一度点(删断路)
-
缩二度点(缩串联):即若 \(u\) 节点为二度点,并存在 \(x - u - y\),那么删去 \(u\),连接 \((x, y)\)。
-
删重边(缩并联)
我们称上面的缩图方式为 广义串并联图方法,不难发现这样简化后的图不存在度数 \(\le 2\) 的点,于是有 \(3n \ge 2m\)。那么假若 \(m - n \le k\),则这样的按这个规则缩图之后就会满足 \(n \le 2k\),\(m \le 3k\)。即图会变成 \(O(k)\) 级别的。值得一提的是,缩图之后 每条边 实际上是原图的某一个 子图,因此一般在缩边的过程中对边进行 \(\rm DP\)。
在代码实现上,一般来说会把 缩二度点 和 删重边 放在一起写,并使用队列维护度数 \(\le 2\) 的点,用 \(\mathrm {map}\) 维护边集,这是由于若原图中没有重边,那么后面的重边只有可能是由缩二度点产生的。
P6790 SNOI2020 生成树
首先注意到仙人掌不会出现同胚于杏仁图的子图,因此加一条边后也不会出现同胚于 \(\rm K4\) 的子图,即这个图是 广义串并联图,考虑在上述的缩图方法中计算方案数 \(ans\)。设 \(f_e\) 是 \(e\) 这条边所代表的子图中两端的点连通的生成树个数,\(g_e\) 是子图中两端的点不连通,但是两端的点所在的生成树覆盖了所有节点的方案数。
-
删掉一度点 \(u\):考虑与其相连的边 \(e\),那么 \(u - e\) 相当于是独立的一个 子图,于是直接让 \(ans \gets {ans \times f_e}\) 即可。
-
缩二度点 \(u\) 所在的链 \(x - u - y\):设 \(e_1 = (x, u), e_2 = (u, y)\),\(e\) 为新建的边 \((x, y)\),那么由于 \(u\) 至少与 \(x, y\) 中的一者连通,所以 \(g_e = f_{e_1} g_{e_2} + f_{e_2}g_{e_1}, f_e = f_{e_1}f_{e_2}\)。
-
删重边 \(e_1, e_2 = (x, y)\):那么两条边不能都选,且两条边任选一条就可以连通 \((x, y)\),因此 \(f_e = f_{e_1}g_{e_2} + f_{e_2}g_{e_1}, g_e = g_{e_1} g_{e_2}\)。
时间复杂度 \(O(n \log n)\)。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 4e5 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
map<int, int> G[N];
ll f[N], g[N], ans = 1;
int n, m, tot, deg[N];
//#define int long long
queue<int> Q;
void upd(int u){
if(deg[u] <= 2) Q.push(u);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= m; i++){
int x, y; cin >> x >> y;
if(!G[x][y]) G[x][y] = G[y][x] = ++tot, f[tot] = g[tot] = 1, deg[x]++, deg[y]++;
else f[G[x][y]]++;
}
for(int i = 1; i <= n; i++) if(deg[i] <= 2) Q.push(i);
while(!Q.empty()){
int u = Q.front(); Q.pop();
if(deg[u] == 0) continue;
if(deg[u] == 1){
int v = (*G[u].begin()).first, cv = (*G[u].begin()).second;
G[v].erase(u); G[u].erase(v); deg[u]--; deg[v]--; upd(v);
MUL(ans, f[cv]);
} else{
int x = (*G[u].begin()).first, cx = (*G[u].begin()).second; G[u].erase(x); G[x].erase(u); deg[x]--, deg[u]--;
int y = (*G[u].begin()).first, cy = (*G[u].begin()).second; G[u].erase(y); G[y].erase(u); deg[y]--; deg[u]--;
ll nf = f[cx] * f[cy] % mod, ng = ((f[cx] * g[cy] % mod) + (f[cy] * g[cx] % mod)) % mod;
int nc;
if(G[x].find(y) != G[x].end()){
nc = G[x][y];
f[nc] = (f[nc] * ng % mod + nf * g[nc] % mod) % mod;
g[nc] = g[nc] * ng % mod;
} else{
G[x][y] = G[y][x] = nc = ++tot; deg[x]++; deg[y]++;
f[nc] = nf; g[nc] = ng;
} upd(x); upd(y);
}
} cout << ans;
return 0;
}
Pakencamp2018 DAY2 G Grand Graph
首先注意到 \(n - m \le 3\),于是考虑 广义串并联图方法,根据结论,这样缩点之后的图至多有 \(6\) 个点,\(9\) 条边,直接爆搜即可。那么考虑在缩图的过程中 \(\rm DP\) 算出方案数。设 \(f_e/g_e\) 为满足边 \(e\) 两端点颜色不同/相同这个子图的方案数 且 不考虑 两端具体的颜色是什么。初始 \(f_e = 1, g_e = 0\)。
-
删一度点 \(u\):设相邻的点为 \(v\),且 \(e = (u, v)\)。那么加入 \(u, v\) 颜色不同,\(u\) 就有 \(k - 1\) 种选择,否则已经确定。于是 \(ans \gets ans \times ((k - 1)f_e + g_e)\)。
-
缩二度点 \(u\) 以及链 \(x - u - y\):
令 \(e_1 = (x, u), e_2 = (u, y), e = (x, y)\),这个地方的系数只需要从 \(u\) 贡献即可,剩下 \(x, y\) 以后考虑。-
\(f_e\) 的转移:若 \(c_x = c_u\),则 \(c_x \neq c_y\) 等价于 \(c_y \neq c_u\),方案数即 \(f_{e_1} g_{e_2}\),以及对称的 \(f_{e_2}g_{e_1}\)。若 \(c_x \neq c_u\),那么若 \(x, y\) 确定,\(u\) 就只有 \(k - 2\) 中选择,方案数就是 \((k - 2)f_{e_1}f_{e_2}\)。
-
\(g_e\) 的转移:首先可以 \(c_x = c_u = c_y\),方案数为 \(g_{e_1}g_{e_2}\),也可以 \(c_u \neq c_x, c_u \neq c_y\),此时若 \(x, y\) 确定,\(u\) 有 \(k - 1\) 种选择,方案数为 \((k - 1)f_{e_1}f_{e_2}\)
-
-
删重边:对应相乘即可。
时间复杂度 \(O(n \log n + 6^6 \times 9)\)。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
const ll mod = 1e9 + 7;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
//#define int long long
map<int, int> G[N];
queue<int> Q;
ll f[M], g[M], k, res;
int n, m, deg[N], tot, col[N], nd[N], pos[N];
void upd(int u){
if(deg[u] <= 2) Q.push(u);
}
void addans(ll ret){
for(int i = 1; i <= nd[0]; i++){
int u = nd[i];
for(auto it : G[u]){
int v = it.first, cv = it.second;
if(v > u) continue;
if(col[pos[u]] == col[pos[v]]) MUL(ret, g[cv]);
else MUL(ret, f[cv]);
}
} ADD(res, ret);
}
void dfs(int step, int cnt, ll mul){
if(step == nd[0] + 1){addans(mul); return;}
for(int i = 1; i <= cnt; i++) col[step] = i, dfs(step + 1, cnt, mul);
if(cnt < k) col[step] = ++cnt, dfs(step + 1, cnt, mul * (k - cnt + 1) % mod);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m >> k; ll ans = 1;
for(int i = 1; i <= m; i++){
int x, y; cin >> x >> y;
if(!G[x][y]) G[x][y] = G[y][x] = ++tot, f[tot] = 1, deg[x]++, deg[y]++;
}
for(int i = 1; i <= n; i++) if(deg[i] <= 2) Q.push(i);
while(!Q.empty()){
int u = Q.front(); Q.pop();
if(deg[u] == 0) continue;
if(deg[u] == 1){
int v = (*G[u].begin()).first, cv = (*G[u].begin()).second;
G[u].erase(v); deg[u]--; G[v].erase(u); deg[v]--;
MUL(ans, ((k - 1) % mod * f[cv] % mod + g[cv]) % mod);
//cerr << f[cv] << " " << ans << "\n";
upd(v);
}
if(deg[u] == 2){
int x = (*G[u].begin()).first, cx = (*G[u].begin()).second; G[u].erase(x); G[x].erase(u); deg[x]--; deg[u]--;
int y = (*G[u].begin()).first, cy = (*G[u].begin()).second; G[u].erase(y); G[y].erase(u); deg[y]--; deg[u]--;
ll nf = ((f[cx] * g[cy] % mod + f[cy] * g[cx] % mod) % mod + (k - 2) % mod * f[cx] % mod * f[cy] % mod) % mod, ng = (g[cx] * g[cy] % mod + f[cx] * f[cy] % mod * (k - 1) % mod) % mod;
if(G[x].find(y) != G[x].end()) MUL(f[G[x][y]], nf), MUL(g[G[x][y]], ng), upd(x), upd(y);
else{
int nc = ++tot; G[x][y] = G[y][x] = nc; deg[x]++; deg[y]++;
f[nc] = nf; g[nc] = ng; upd(x); upd(y);
}
}
//cerr << u << " " << ans << "\n";
}
for(int i = 1; i <= n; i++) if(deg[i] >= 3) nd[++nd[0]] = i, pos[i] = nd[0];
dfs(1, 0, 1);
if(!nd[0]) cout << k * ans % mod;
else cout << res * ans % mod;
return 0;
}
P4426 HNOI/AHOI2018 毒瘤
- 题意:给一张 \(n \le 10^5, m - n \le 10\) 的无向图,问其独立集方案数对 \(998244353\) 取模后的值。
还是像上面那样考虑在缩边的时候计数,设 \(f_{e, c_0, c_1}\) 为边 \(e\) 两端的选择情况是 \((c_0, c_1)\) 中间子图独立集的方案数,缩重边直接乘起来,缩二度点暴力卷积,但是删一度点并不能直接算进答案里,原因是这个一度点的贡献并不是固定的。那么考虑记录一个点 \(u\) 选 / 不选时,该点所代表的一度点子图的方案数为 \(g_{u, 0 / 1}\)。
考虑如何转移:
-
删一度点 \(u\):令 \(e = (u, v)\),\(g_u\) 的转移暴力卷积即可,即 \(g_{v, c_v} = \sum_{c_u \in \{0, 1\}} {g_{u, c_u} \times f_{e, c_u, c_v}}\)。
-
缩二度点 \(u\):还是直接暴力卷积即可,但是 \(u\) 还带一个 \(g_{u, c_u}\) 的系数。
-
缩重边:依次乘起来即可。
最后再使用 \(O(d2^{2d}), d = m - n\) 的枚举即可。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 2e5 + 10, M = 4e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
//#define int long long
map<int, int> G[N];
queue<int> Q;
int n, m, deg[N], tot, nd[N], pos[N], del[N];
ll f[M][2][2], g[N][2];
void upd(int u){if(deg[u] <= 2) Q.push(u);}
void add_edge(int x, int y, ll a, ll b, ll c, ll d){
if(!G[x][y]) G[x][y] = ++tot, deg[x]++, f[tot][0][0] = a, f[tot][0][1] = b, f[tot][1][0] = c, f[tot][1][1] = d;
else{
int nc = G[x][y];
MUL(f[nc][0][0], a); MUL(f[nc][0][1], b); MUL(f[nc][1][0], c); MUL(f[nc][1][1], d);
}
}
void deledge(int x, int y){
G[x].erase(y); G[y].erase(x); deg[x]--; deg[y]--;
}
bool ex(int S, int i){return (S & (1ll << i));}
vector<pir> newG[N];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= m; i++){
int x, y; cin >> x >> y;
add_edge(x, y, 1, 1, 1, 0);
add_edge(y, x, 1, 1, 1, 0);
}
for(int i = 1; i <= n; i++) upd(i), g[i][0] = g[i][1] = 1;
while(!Q.empty()){
int u = Q.front(); Q.pop();
if(deg[u] == 0) continue;
if(deg[u] == 1){
int v = (*G[u].begin()).first, cv = (*G[u].begin()).second;
deledge(u, v);
for(int c0 = 0; c0 < 2; c0++){
ll ret = 0;
for(int c1 = 0; c1 < 2; c1++) ADD(ret, g[u][c1] * f[cv][c1][c0] % mod);
MUL(g[v][c0], ret);
}
upd(v); del[u] = 1;
}
if(deg[u] == 2){
int x = (*G[u].begin()).first, cx = (*G[u].begin()).second; deledge(u, x);
int y = (*G[u].begin()).first, cy = (*G[u].begin()).second; deledge(u, y);
ll tmp[2][2]; memset(tmp, 0, sizeof tmp);
for(int cu = 0; cu < 2; cu++)
for(int c0 = 0; c0 < 2; c0++)
for(int c1 = 0; c1 < 2; c1++)
ADD(tmp[c0][c1], g[u][cu] * f[cx][cu][c0] % mod * f[cy][cu][c1] % mod);
add_edge(x, y, tmp[0][0], tmp[0][1], tmp[1][0], tmp[1][1]);
add_edge(y, x, tmp[0][0], tmp[1][0], tmp[0][1], tmp[1][1]);
upd(x); upd(y); del[u] = 1;
}
}
for(int i = 1; i <= n; i++) if(!del[i]) nd[++nd[0]] = i, pos[i] = nd[0];
for(int i = 1; i <= nd[0]; i++){
int u = nd[i];
for(auto it : G[u]){
int v = it.first; if(v < u) continue;
newG[i].pb(mkpir(pos[v], it.second));
}
}
ll ans = 0;
for(int S = 0; S < (1ll << nd[0]); S++){
ll res = 1;
for(int i = 1; i <= nd[0]; i++){
MUL(res, g[nd[i]][ex(S, i - 1)]);
for(auto p : newG[i]){
int v = p.first, cv = p.second;
MUL(res, f[cv][ex(S, i - 1)][ex(S, v - 1)]);
}
} ADD(ans, res);
} cout << ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号