多项式基础内容小记
0. 基础知识:
关于多项式的定义:
-
多项式:一个形如 \(f(x) = \sum_{i = 0} ^n a_i x^i\) 的有限和式被称为多项式。
-
系数:多项式第 \(i\) 项的系数在上面就表示为 \(a_i\)。
-
度(次数):多项式中最高次数的项的次数就被称为该多项式的度,也称次数。
多项式表示法:
多项式有两种表示法:分别是 系数表示法 和 点值表示法。其中系数表示法就形如上面给出的形式。
而点值表示法则是用不同的 \(n + 1\) 个点来表示一个 \(n\) 次多项式。其中 两点确定一条直线 就是一个很好的例子。如何快速的在两者中快速转化呢?这是我们要研究的问题。其中从点值表示法到系数表示法的过程叫插值,从系数表示法到点值表示法的过程叫求值。
1.拉格朗日插值:
这个东西的作用其实很大,可以用来优化在值域上很大,但是 转移与值域无关 或 转移都是简单加乘 的 \(\rm DP\),此时这个 \(\rm DP\) 值其实是关于值域的一个多项式,若可以归纳证明它是一个 有限次数且次数较小 的多项式,可以拉插优化。
接下来先研究一下如何快速插值。首先一个简单的想法是直接列出 \(n + 1\) 条方程式并使用高斯消元,但这样是 \(O(n^3)\) 的,能不能更快呢?
我们尝试换一种多项式的表现方式:考虑给每个 \(y_i\) 前面都加上一个系数 \(k_i\) 并求和,并当 \(x = x_i\) 时该 \(k_i\) 取到 \(1\),对于其他的情况取到 \(0\)。但这样还是比较困难的,注意到我们只关心该多项式的表达式在这 \(n + 1\) 的表现,于是考虑将 \(k_i\) 的定义变为:当 \(x\) 为任意 \(x_j(j \ne i)\) 时,\(k_i\) 取到 \(0\),其他情况取到 \(1\)。形式化的:令 \(f(x) = \sum_{i = 1} ^ {n + 1} k_iy_i\),其中 \(k_i = [\forall j(1 \le j \le n + 1, j \ne i), x \ne x_j]\)。
于是我们只需要构造出合适的 \(k_i\) 满足上述条件即可,显然 \(\prod_{j \ne i} (x - x_j)\) 会在 \(x\) 取到任意 \(x_j, j \ne i\) 时取到 \(0\),但是当 \(x = x_i\) 时,该式子不是 \(1\),那就把多出来的除掉即可。于是得到 \(k_i = \prod_{j \ne i} \frac{x-x_j}{x_i-x_j}\)。于是 \(f(x) = \sum_{i = 1}^{n + 1}y_i \prod_{j \ne i} \frac{x-x_j}{x_i-x_j}\)。算法时间复杂度降到了 \(O(n^2)\),这便是拉格朗日插值。
值得一提的是,若 \(x\) 值连续,如 \(x_i = i\),那么不难发现柿子上下都是某个阶乘扣掉一个数,预处理阶乘和逆元容易做到 \(O(n)\)。
P4781 【模板】拉格朗日插值
qwq
#include<bits/stdc++.h>
#define int long long
#define inv(x) qpow(x, mod - 2)
using namespace std;
const int N = 2e3 + 10, mod = 998244353;
int n, k, ans;
struct point{
int x, y;
}p[N];
int qpow(int x, int y){
int ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> p[i].x >> p[i].y;
for(int i = 1; i <= n; i++){
int sum1 = p[i].y, sum2 = 1;
for(int j = 1; j <= n; j++){
if(i == j) continue;
sum1 = (sum1 * ((k - p[j].x + mod)) % mod) % mod;
sum2 = (sum2 * ((p[i].x - p[j].x + mod) % mod)) % mod;
}
ans = (ans + sum1 * inv(sum2) % mod) % mod;
}
cout << ans;
// system("pause");
return 0;
}
2.快速傅里叶变换(FFT)
接下来研究如何快速对多项式做乘法,其实也就是如何快速对两个系数数列做卷积。首先暴力卷积显然是 \(O(n^2)\) 的,很不好,考虑如何优化这个过程。
两个多项式乘法是 \(O(n^2)\) 的,但是把两个多项式不同的 \(n\) 个点值乘起来是 \(O(n)\) 的。于是现在我们可以把乘法拆成三个步骤:
-
对于一个 \(n\) 次多项式 \(A\),找到任意 \(x_0, x_1 ..., x_n\), 求出 \(A(x_0), A(x_1) ..., A(x_n)\)。\(B\) 同理。\((\rm DFT)\)
-
求出 \(C_i = A(x_i) \times B(x_i)\)
-
通过 \(C_{0, 1, ..., n + m}\) 插值插出 \(C\) 的系数序列。\((\rm IDFT)\)
DFT
先考虑 \(\rm DFT\) 如何做。首先考虑分治划分子问题,我们把 \(F\) 奇偶拆半,即 \(F(x) = F_e(x^2) + xF_o(x^2)\),其中 \(F_e\) 含 \(F\) 中的偶次数项,\(F_o\) 含 \(F\) 中的奇数次数项。但是对于每个 \(x\) 如果每次都这样做一次,显然太慢了。我们希望在同一层的 \(F_e, F_o\) 每次都可以重复利用以减小时间复杂度,但这样就要求 \(x\) 序列有一些特殊的性质。
这个时候就需要单位根啦!定义 \(n\) 次单位根 \(\omega_n = \cos(\frac{2\pi}{n}) + i\sin(2\pi)\),其实就是复平面单位圆上 \(n\) 等分的结果,他的 \(k\) 次方就相当于在上面转了 \(\frac{2\pi k}{n}\) 的弧度。(这个是因为复数相乘,模长相乘,幅角相加,在单位圆上模长都是 \(1\))。因此有以下结论:
-
\(\omega_n^{2k} = \omega_{n / 2}^k\)
-
\(\omega_n^{n + k} = \omega_n^{k}\)
-
\(\omega_n^{\frac{n}{2} + k} = -\omega_n^{k}\),其中 \(2 | n\)
这些性质均可以通过在单位圆上旋转来理解。
于是我们考虑到单位根的特殊性质,不妨直接令 \(x_i = \omega_n^{i}\),其中 \(n\) 是不小于多项式次数的最小 \(2\) 的整数次幂。(原因下面会讲)
那么 \(F(\omega_n^i) = F_e(\omega_{\frac{n}{2}}^i) + \omega_n^i F_o(\omega_{\frac{n}{2}}^i)\)。
这里用到了第一个性质,每次都要满足 \(2 | n\),因此分治树上的每一层 \(n\) 都应该为偶数,那么 \(n\) 显然需要是一个 \(2\) 的整数次幂。然后不难发现,这里需要的分治下去的点值我们都已经求出来了,相当于一个子问题,时间复杂度 \(T(n) = 2T(n / 2) + O(n)\),即 \(T(n) = O(n \log n)\)。
优化
先不急着讲 \(\rm IDFT\),可以看到 \(\rm FFT\) 的常数是非常大的其中精度问题也有。那么接下来给出一个常见的优化:蝴蝶变换。
考虑 \(\rm DFT\) 的过程:
-
把 \(a_i\) 的贡献向两边分,即从上至下的建立分治树
-
从下往上的合并两个儿子的信息。
考虑画出这个分治树:
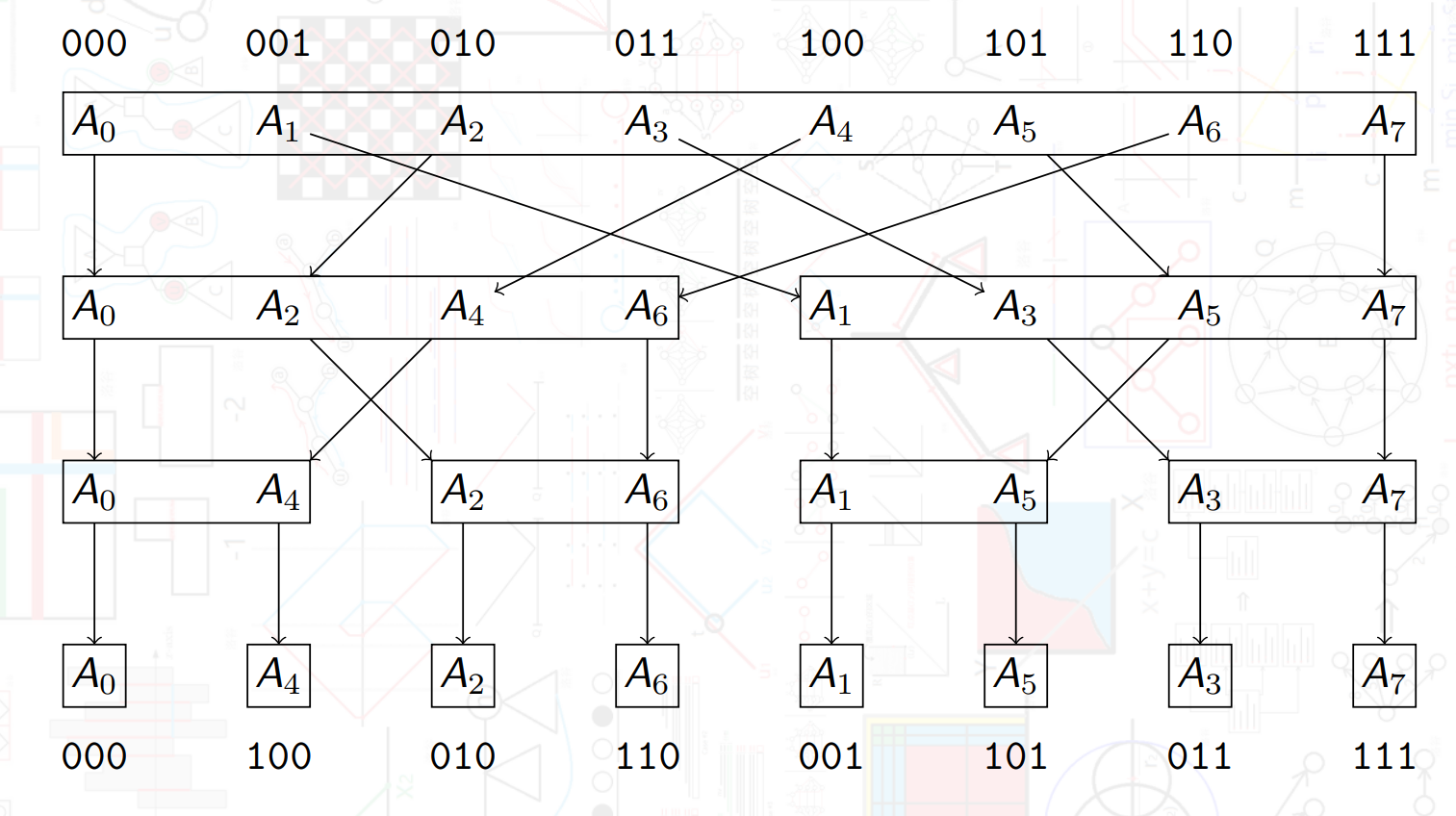
(不会画图就偷了一张/lh)
可以看到对于一个数 \(i\),最后在根节点上表现出来的位置是 \(rev(i)\),\(rev(i)\) 表示把 \(i\) 的二进制位翻转,比如 \(011\) 变为 \(110\)。那么不妨直接把这个东西提前交换过来。这样就不需要 \(O(n \log n)\) 的建树了,然后算答案时可以直接从下往上迭代,避免 \(\mathrm {vector}\) 传递带来的巨大开销。
IDFT
考虑 \(\rm DFT\) 的转移矩阵:
对其求逆可以得到:
那么 \(\rm IDFT\) 就相当于把一个点值组成的向量乘上这个逆矩阵,其实就是 \(\rm DFT\),只不过值不一样。但是由于 \(\omega_n^{-i} = \omega_n{n - i}\),那么只需要对求出来的点值序列先做一遍正常的 \(\rm DFT\),然后翻转一下就可以了。
至此,多项式乘法就可以在 \(O(n \log n)\) 时间解决了。
qwq
#include<bits/stdc++.h>
#define ll long long
#define db double
using namespace std;
const int N = 1 << 21 | 50;
const db pai = acos(-1);
struct CP{
db a, b; // a + bi
CP(db x = 0, db y = 0){a = x; b = y;}
CP operator +(CP x){return CP(a + x.a, b + x.b);}
CP operator -(CP x){return CP(a - x.a, b - x.b);}
CP operator *(CP x){return CP(a * x.a - b * x.b, a * x.b + b * x.a);}
CP operator /(int x){return CP(a / x, b / x);}
}w[N];
using Poly = vector<CP>;
int rev[N];
void init(int n){
for(int i = 2; i <= n; i <<= 1){
const int ls = i >> 1;
for(int k = 0; k < n / 2; k++)
w[ls + k] = CP(cos(2 * pai * k / i), sin(2 * pai * k / i));
}
const int mid = n >> 1;
for(int i = 1; i < n; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? mid : 0);
}
void DFT(Poly &F){
const int n = F.size();
for(int i = 0; i < n; i++) if(i < rev[i]) swap(F[i], F[rev[i]]);
for(int i = 2; i <= n; i <<= 1){
const int mi = i >> 1;
for(int j = 0; j < n; j += i){
for(int k = 0; k < mi; k++){
CP qwq = w[mi + k] * F[j + k + mi];
F[j + k + mi] = F[j + k] - qwq; F[j + k] = F[j + k] + qwq;
}
}
}
}
void IDFT(Poly &F){
DFT(F); int n = F.size();
reverse(&F[1], &F[n]);
for(int i = 0; i < n; i++) F[i] = F[i] / n;
}
Poly operator *(Poly A, Poly B){
int resiz = A.size() + B.size() - 1, n;
for(n = 1; n < resiz; n <<= 1);
A.resize(n); B.resize(n); init(n);
DFT(A); DFT(B);
for(int i = 0; i < n; i++) A[i] = A[i] * B[i];
IDFT(A); return A;
}
#define gc getchar()
int read(){
char c = gc; int x = 0;
while(c < '0' || c > '9') c = gc;
while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = gc;
return x;
}
void _out(int x){
if(!x) return;
_out(x / 10); putchar(x % 10 + '0');
}
void print(int x, char sp){
_out(x);
if(x == 0) putchar('0'); putchar(sp);
}
signed main(){
int n, m; n = read(); m = read();
Poly A(n + 1), B(m + 1);
for(int i = 0; i <= n; i++) A[i].a = read();
for(int i = 0; i <= m; i++) B[i].a = read();
Poly C = A * B;
for(int i = 0; i <= n + m; i++) print((int)(C[i].a + 0.1), ' ');
return 0;
}
3. FMT/FWT
我们拓展一下卷积的形式,变为位运算卷积。即 or, and, xor。即给出多项式 \(A = (a_0, a_1 \dots a_n), B = (b_0, b_1, \dots b_n)\),求出 \(C = (c_0, c_1, \dots c_n)\),其中 \(c_i = \sum_{j \oplus k} a_j \times a_k\)。\(\oplus\) 为 or, and, xor 中的一种。
我们类似 FFT 的思路,设计一个变换 \(F(A) \to B\),和其逆变换 \(iF(B) \to A\),满足 \(F, iF\) 都可以快速计算,同时还要满足 \(F(A) \times F(B) = F(A \oplus B)\)。
首先注意到 or 和 and 都是相类似的,从高维视角看,一个是集合的并集而一个是集合的交集。下文考虑 or,那么我们考虑类似容斥的东西,设计 \(F(A) = \sum_{S' \subseteq A} a_{S'}\),那么容易有 \(F(A) \times F(B) = F(C)\)。那么考虑 \(iF(A)\) 的求法,这个容易有 \(iF(A) = \sum_{S' \subseteq A} (-1)^{|A - S'|} a_{S’}\)。
考虑如何快速求出 \(F(A)\),我们从底到高依次考虑每一位 \(i\),那么此时对于 \(i - 1\) 位以下的卷积已经做好了,直接对第 \(i\) 位做卷积即可,那么此时只要让该位为 \(1\) 的加上对应的该位为 \(0\) 的即可。时间复杂度 \(O(n \log n)\)。
对于 \(iF\) 的话,这个就相当于每次加入一个 \(0\) 就要乘上 \(-1\),那么此时就相当于该位为 \(1\) 的减去该位为 \(0\) 的。其他都是一样的。
对于 and 来说也是一样的,只不过换成后缀和。
这上面的都是基于 \(F\) 是高维前/后缀和的变换,该变换叫做 \(\rm FMT\)(莫比乌斯变换)。而对于 xor 的形式比较特殊,会给出另一种形式的变换,叫做 \(\rm FWT\)(快速沃尔士变换)。
(可以跳过这段)
还是考虑如何构造一个函数,即考虑构造 \(F(A) \times F(B) = F(A \operatorname{xor} B)\)。这里有一个人类智慧。令 \(h(a) = \operatorname{popcnt}(a) \bmod 2\),则有 \(h(a \operatorname{and} c) \operatorname{xor} h(b \operatorname{and} c) = h((a \operatorname{xor} b) \operatorname{and} c)\),这是因为 \(a \operatorname{xor} b\) 只会让原来有贡献的位要么贡献 -2 要么不变。也就是假设 \(g(a, b) = (\operatorname{popcnt}(a \operatorname{and} b) \bmod 2)\),则 \((g, \operatorname{xor})\) 具有结合律。那么对于 \(F\) 来说,我们要求的是 \((\times, \operatorname{xor})\) 具有交换律,我们该如何做一个 \(g(a, b) \to \times\) 的映射呢?可以考虑放到系数上。
具体的,我们构造 \(F(A) = \sum_{S} (-1)^{|S \cap A|} a_S\)。下面证明 \(F(A) \times F(B) = F(A \operatorname{xor} B)\)。(这里的 \(\operatorname{xor}\) 指的是异或卷积后的结果)。我们下面只考察某个集合 \(S\) 在 \(F(A \operatorname{and} B)\) 的表现。
那么最关键的构造就搞好了。还是类似 \(\rm FMT\) 的思路,考虑第 \(i\) 位如何合并答案,注意到当选择的两个集合该位都为 \(1\) 时 \(-1\) 才会产生贡献。于是相当于 \(0 = 0 + 1\), \(1 = 0 - 1\)。然后考虑 \(iF\) 的计算方式。对这个东西求逆还是比较抽象的,反正我不会,结论是乘上 \(\frac{1}{n}\) 就好了。
模板题代码
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define se second
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
#define ull unsigned long long
#define umap unordered_map
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10;
const ll mod = 998244353, iv2 = (mod + 1) / 2ll;
/*
struct edge{
int v, next;
}edges[M << 1];
int head[N], idx;
void add_edge(int u, int v){
edges[++idx] = {v, head[u]};
head[u] = idx;
}
*/
il ll qpow(ll x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void chkmod(ll& x){x = (x + mod) % mod;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
//#define int long long
struct Poly{
int n, K;
ll a[N]; // op = 1 : fmt/fwt, op = -1 : ifmt/ifwt
void fmt_or(ll op){
chkmod(op);
for(int k = 1; k < n; k <<= 1)
for(int i = 0; i < n; i += (k << 1))
for(int j = 0; j < k; j++)
ADD(a[i + j + k], a[i + j] * op % mod);
}
void fmt_and(ll op){
chkmod(op);
for(int k = 1; k < n; k <<= 1)
for(int i = 0; i < n; i += (k << 1))
for(int j = 0; j < k; j++)
ADD(a[i + j], a[i + j + k] * op % mod);
}
void fwt_xor(ll op){
if(op == -1) op = iv2;
for(int k = 1; k < n; k <<= 1)
for(int i = 0; i < n; i += (k << 1))
for(int j = 0; j < k; j++){
ll a0 = a[i + j], a1 = a[i + j + k];
a[i + j] = op * (a0 + a1) % mod;
a[i + j + k] = op * (a0 - a1 + mod) % mod;
}
}
};
Poly operator |(Poly P1, Poly P2){
//cerr << 1 << "\n";
P1.fmt_or(1); P2.fmt_or(1);
Poly ret; ret.n = P1.n;
for(int i = 0; i < ret.n; i++) ret.a[i] = P1.a[i] * P2.a[i] % mod;
ret.fmt_or(-1); return ret;
}
Poly operator &(Poly P1, Poly P2){
P1.fmt_and(1); P2.fmt_and(1);
Poly ret; ret.n = P1.n;
for(int i = 0; i < ret.n; i++) ret.a[i] = P1.a[i] * P2.a[i] % mod;
ret.fmt_and(-1); return ret;
}
Poly operator ^(Poly P1, Poly P2){
P1.fwt_xor(1); P2.fwt_xor(1);
Poly ret; ret.n = P1.n;
for(int i = 0; i < ret.n; i++) ret.a[i] = P1.a[i] * P2.a[i] % mod;
ret.fwt_xor(-1); return ret;
}
ostream& operator <<(ostream &out, Poly P){
for(int i = 0; i < P.n; i++) out << P.a[i] << " ";
out << "\n"; return out;
}
istream& operator >>(istream &in, Poly &P){
for(int i = 0; i < P.n; i++) in >> P.a[i];
return in;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
Poly A, B;
cin >> A.K; B.K = A.K; A.n = B.n = (1 << A.K);
cin >> A >> B;
cout << (A | B) << (A & B) << (A ^ B);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号