点分治复习笔记
1.Tree
Description:
求一棵树中长度不超过\(K\)的路径条数
Solution:
直接统计深度,由于深度的贡献具有单调性
考虑每次统计答案时先排序,然后双指针每次相减
这样就比\(n^2\)统计优秀多了,记得要减掉算重的
2.[模版]点分治1
Description:
求一棵树中是否存在长度为\(K\)的链,\(m\)组询问,\(m \le 100\)
Solution:
考虑每次用桶把路径长度标记,把所有询问在桶里查一遍,再清空桶
复杂度\(O(nmlog^2n)\)
#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1
#define rs p<<1|1
using namespace std;
typedef long long ll;
const int mxn=1e5+5,inf=1e7;
int n,m,s,rt,cnt,tot,sumsz,f[mxn],hd[mxn],sz[mxn],vis[mxn],dis[mxn],ask[mxn],ans[mxn],tag[mxn],dep[mxn],bac[inf+5];
inline int read() {
char c=getchar(); int x=0,f=1;
while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
return x*f;
}
inline void chkmax(int &x,int y) {if(x<y) x=y;}
inline void chkmin(int &x,int y) {if(x>y) x=y;}
struct ed {
int to,nxt,w;
}t[mxn<<1];
inline void add(int u,int v,int w) {
t[++cnt]=(ed) {v,hd[u],w}; hd[u]=cnt;
}
int getrt(int u,int fa) {
sz[u]=1; f[u]=0;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
getrt(v,u); sz[u]+=sz[v];
chkmax(f[u],sz[v]);
}
chkmax(f[u],sumsz-sz[u]);
if(f[u]<f[rt]) rt=u;
}
void getdis(int u,int fa) {
dis[++tot]=dep[u];
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
dep[v]=dep[u]+t[i].w; getdis(v,u);
}
}
void cal(int u) {
s=0;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(vis[v]) continue ;
dep[v]=t[i].w; tot=0; getdis(v,u);
for(int j=1;j<=m;++j) {
for(int k=1;k<=tot;++k) {
if(dis[k]>ask[j]) break ;
ans[j]|=bac[ask[j]-dis[k]];
}
}
for(int k=1;k<=tot;++k)
if(dis[k]<=inf) bac[dis[k]]=1,tag[++s]=dis[k];
}
for(int i=1;i<=s;++i) bac[tag[i]]=0; bac[0]=1;
}
void solve(int u) {
vis[u]=1; cal(u);
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(vis[v]) continue ;
sumsz=sz[v]; rt=0;
getrt(v,u); solve(rt);
}
}
int main()
{
n=read(); m=read(); int u,v,w; bac[0]=1;
for(int i=1;i<n;++i) {
u=read(); v=read(); w=read();
add(u,v,w); add(v,u,w);
}
for(int i=1;i<=m;++i) ask[i]=read();
rt=0; sumsz=f[0]=n; getrt(1,0); solve(rt);
for(int i=1;i<=m;++i)
if(ans[i]) puts("AYE"); else puts("NAY");
return 0;
}
3.聪聪可可
Description:
给你一棵树,询问有多少条路径满足边权和为3的倍数
Solution:
和Tree差不多......统计时开3个桶,乘法原理搞一下就行
4.Distance in Tree
Description:
给你一棵树,问路径长为K的条数
Solution:
方法同2,如果你无聊的话可以写个类似Tree的写法用<=k的减去<k的
居然跑了rk5?
#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1
#define rs p<<1|1
using namespace std;
typedef long long ll;
const int mxn=1e5+5;
int n,m,k,rt,cnt,tot,ans,sumsz,f[mxn],hd[mxn],sz[mxn],bac[mxn],dep[mxn],vis[mxn],dis[mxn];
inline int read() {
char c=getchar(); int x=0,f=1;
while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
return x*f;
}
inline void chkmax(register int &x,register int y) {if(x<y) x=y;}
inline void chkmin(register int &x,register int y) {if(x>y) x=y;}
struct ed {
int to,nxt,w;
}t[mxn<<1];
inline void add(register int u,register int v,register int w) {
t[++cnt]=(ed) {v,hd[u],w}; hd[u]=cnt;
}
int getrt(register int u,register int fa) {
f[u]=0; sz[u]=1;
for(register int i=hd[u];i;i=t[i].nxt) {
register int v=t[i].to;
if(v==fa||vis[v]) continue ;
getrt(v,u); sz[u]+=sz[v];
chkmax(f[u],sz[v]);
}
chkmax(f[u],sumsz-sz[u]);
if(f[rt]>f[u]) rt=u;
}
void getdis(register int u,register int fa) {
if(dep[u]<=k) ++dis[dep[u]],ans+=bac[k-dep[u]];
for(register int i=hd[u];i;i=t[i].nxt) {
register int v=t[i].to;
if(v==fa||vis[v]) continue ;
dep[v]=dep[u]+t[i].w; getdis(v,u);
}
}
void cal(register int u) {
tot=0;
for(register int i=hd[u];i;i=t[i].nxt) {
register int v=t[i].to;
if(vis[v]) continue ;
dep[v]=t[i].w; getdis(v,u);
for(register int j=1;j<=k;++j)
bac[j]+=dis[j],dis[j]=0;
}
for(register int i=1;i<=k;++i) bac[i]=0;
}
void solve(register int u) {
cal(u); vis[u]=1;
for(register int i=hd[u];i;i=t[i].nxt) {
register int v=t[i].to;
if(vis[v]) continue ;
rt=0; sumsz=sz[v];
getrt(v,u); solve(rt);
}
}
int main()
{
n=read(); k=read(); register int u,v,w; bac[0]=1;
for(register int i=1;i<n;++i) {
u=read(); v=read(); w=1;
add(u,v,w); add(v,u,w);
}
rt=0; sumsz=f[0]=n;
getrt(1,0); solve(rt);
printf("%d",ans);
return 0;
}
5.[IOI2011] Race
Description:
求树上的一条路径,长度为K且边最少
Solution:
其实也很简单,就用Tree的方法直接计数,然后减去
不同的是,要把答案扔到一个边数桶里
https://www.cnblogs.com/candy99/p/6270581.html
6.树上游戏
Description:
lrb有一棵树,树的每个节点有个颜色。给一个长度为n的颜色序列,定义s(i,j) 为i 到j 的颜色数量。以及
现在他想让你求出所有的sum[i]
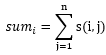
Solution:
毒瘤题,考虑第一次碰到一种颜色会产生该点子树的贡献
看代码吧:
#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1
#define rs p<<1|1
using namespace std;
typedef long long ll;
const int mxn=1e5+5;
int n,m,s,rt,cnt,sumsz,hd[mxn];
int f[mxn],val[mxn],sz[mxn],vis[mxn];
int num[mxn],fs[mxn],col[mxn],tot[mxn];
ll sum,ans[mxn];
inline int read() {
char c=getchar(); int x=0,f=1;
while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
return x*f;
}
inline void chkmax(int &x,int y) {if(x<y) x=y;}
inline void chkmin(int &x,int y) {if(x>y) x=y;}
struct ed {
int to,nxt;
}t[mxn<<1];
inline void add(int u,int v) {
t[++cnt]=(ed) {v,hd[u]}; hd[u]=cnt;
}
int getrt(int u,int fa) {
sz[u]=1; f[u]=0;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
getrt(v,u); sz[u]+=sz[v];
chkmax(f[u],sz[v]);
}
chkmax(f[u],sumsz-sz[u]);
if(f[u]<f[rt]) rt=u;
}
void dfs(int u,int fa,ll &res) {
sz[u]=1; ++num[val[u]];
if(num[val[u]]==1) fs[u]=1,++s;
else fs[u]=0;
tot[u]=s; res+=tot[u];
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
dfs(v,u,res); sz[u]+=sz[v];
}
if(fs[u]) col[val[u]]+=sz[u],sum+=sz[u],--s;
--num[val[u]];
} //单独计算根的答案
void change(int u,int fa,int x) {
if(fs[u]) col[val[u]]+=x*sz[u],sum+=x*sz[u];
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
change(v,u,x);
}
}
void cal(int u,int fa,int k) {
if(fs[u]) sum-=col[val[u]];
ans[u]+=1ll*tot[u]*k+sum; //前者是越过分治中心的贡献,后者是本身子树的
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
cal(v,u,k);
}
if(fs[u]) sum+=col[val[u]];
}
void clear(int u,int fa) {
col[val[u]]=0;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
clear(v,u);
}
}
void solve(int u) {
vis[u]=1; dfs(u,0,ans[u]); col[val[u]]-=sz[u]; sum-=sz[u]; //先减掉根的贡献
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(vis[v]) continue ;
change(v,0,-1); //去除该子树贡献
cal(v,0,sz[u]-sz[v]); //计算该子树答案
change(v,0,1);
}
clear(u,0); sum=0;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(vis[v]) continue ;
sumsz=sz[v]; rt=0;
getrt(v,u); solve(rt);
}
}
int main()
{
n=read(); int u,v;
for(int i=1;i<=n;++i) val[i]=read();
for(int i=1;i<n;++i) {
u=read(); v=read();
add(u,v); add(v,u);
}
f[0]=n; rt=0; sumsz=n;
getrt(1,0); solve(rt);
for(int i=1;i<=n;++i) printf("%lld\n",ans[i]);
return 0;
}
7.[BJOI2017]难题
Description:
每条边有颜色,路径的权值定义为连续颜色段权值的和,求一条长为[L,R]路径的最大权值
Solution:
本来可以直接开桶维护最大值
但是更新答案时要查询一段区间,很烦
考虑类似滑动窗口那题的单调队列优化
或者你也可以写个线段树合并
这题恶心的一点是你要考虑颜色相同时的合并
所以遍历儿子时要把相同颜色边的弄到一起,方便讨论
合并时注意还要按深度启发式合并,保证复杂度
#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1
#define rs p<<1|1
using namespace std;
typedef long long ll;
const int mxn=1e5+5,inf=1e9;
int n,m,L,R,rt,ans,cnt,sumsz,hd[mxn];
int sz[mxn],mx[mxn],dep[mxn],vis[mxn],col[mxn],colmx[mxn],T[mxn],dis[mxn],f[mxn],g[mxn];
inline int read() {
char c=getchar(); int x=0,f=1;
while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
return x*f;
}
inline void chkmax(int &x,int y) {if(x<y) x=y;}
inline void chkmin(int &x,int y) {if(x>y) x=y;}
struct ed {
int to,nxt,w;
}t[mxn<<1];
inline void add(int u,int v,int w) {
t[++cnt]=(ed) {v,hd[u],w}; hd[u]=cnt;
}
void getrt(int u,int fa) {
mx[u]=0; sz[u]=1;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
getrt(v,u); sz[u]+=sz[v];
chkmax(mx[u],sz[v]);
}
chkmax(mx[u],sumsz-sz[u]);
if(mx[rt]>mx[u]) rt=u;
}
void getdep(int u,int fa,int d) {
dep[u]=d;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
getdep(v,u,d+1); chkmax(dep[u],dep[v]);
}
}
void getval(int u,int fa,int val,int las,int d) {
if(d>R) return ;
chkmax(dis[d],val);
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(v==fa||vis[v]) continue ;
getval(v,u,val+(t[i].w!=las)*col[t[i].w],t[i].w,d+1);
}
}
struct Buc {
int col,deep,id;
friend bool operator < (Buc x,Buc y) {
if(x.col==y.col) return x.deep<y.deep;
return colmx[x.col]<colmx[y.col];
}
}A[mxn];
void merge(int *a,int &lena,int *b,int &lenb) {
for(int i=1;i<=max(lena,lenb);++i)
chkmax(a[i],b[i]),b[i]=-inf;
lena=lenb;
}
int cal(int *a,int lena,int *b,int lenb,int val,int flag) {
chkmin(lena,R),chkmin(lenb,R);
static int q[mxn]; int h=1,tl=0,res=-inf;
for(int i=lenb,j=0;i;--i) {
while(j<=lena&&i+j<=R) {
while(h<=tl&&a[q[tl]]<=a[j]) --tl;
q[++tl]=j; ++j;
}
while(h<=tl&&q[h]+i<L) ++h;
if(flag) chkmax(res,T[i]+b[i]);
//在和同色路径合并答案时同时与之前子树算答案
if(h<=tl&&q[h]+i<=R&&q[h]+i>=L)
if(flag) chkmax(res,a[q[h]]-val+b[i]);
else b[i]=a[q[h]]; //处理T数组,表示在i+len在[L,R]的f[i]的max
}
return res;
}
void solve(int u) {
vis[u]=1; int cnts=0;
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(vis[v]) continue ;
getdep(v,u,1); chkmax(colmx[t[i].w],dep[v]);
A[++cnts]=(Buc){t[i].w,dep[v],v};
}
sort(A+1,A+cnts+1); //排序
if(A[cnts].deep*2<L) return ;
int szf=0,szg=0;
for(int i=1;i<=cnts;++i) {
if(i!=1&&A[i].col!=A[i-1].col) {
merge(f,szf,g,szg),szg=0; //g表示同色的路径,f表示不同色的路径
cal(f,szf,T,colmx[A[i].col],0,0);
}
getval(A[i].id,0,col[A[i].col],A[i].col,1);
chkmax(ans,cal(g,szg,dis,A[i].deep,col[A[i].col],1));//多算的要减去
merge(g,szg,dis,A[i].deep);
}
for(int i=1;i<=cnts;++i) colmx[A[i].col]=0;
for(int i=1;i<=A[cnts].deep;++i) {
f[i]=g[i]=-inf;
T[i]=(L<=i&&i<=R)?0:-inf;
}
for(int i=hd[u];i;i=t[i].nxt) {
int v=t[i].to;
if(vis[v]) continue ;
rt=0; sumsz=sz[v];
getrt(v,u); solve(rt);
}
}
int main()
{
int u,v,w; ans=-inf;
n=read(); m=read(); L=read(); R=read();
for(int i=1;i<=m;++i) col[i]=read();
for(int i=1;i<n;++i) {
u=read(); v=read(); w=read();
add(u,v,w); add(v,u,w);
}
memset(f,0x80,sizeof(f));
memset(g,0x80,sizeof(g));
memset(T,0x80,sizeof(T));
memset(dis,0x80,sizeof(dis));
mx[0]=inf; sumsz=n; rt=0; getrt(1,0);
solve(rt); printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号