14.树状数组

14.树状数组

1.构建树状数组

• C[1] = A[1];
• C[2] = A[1] + A[2];
• C[3] = A[3];
• C[4] = A[1] + A[2] + A[3] + A[4];
• C[5] = A[5];
• C[6] = A[5] + A[6];
• C[7] = A[7];
• C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

$C[i]=A[i-2^k+1]+A[i-2^k+2]+...+A[i]$;//k为i的二进制中从最低位到高位连续0的长度

利用$2^k=i\&(-i)$,主要利用负数的存储特性

如下：

• 当x为0时，结果显然为0
• x为奇数，x的最后一个比特位为1，取反加1没有进位，故x和-x最后一位外前面的位正好相反，按位与结果为0.结果为1.
• x为偶数且是2的m次方，x的二进制表示中只有一位是1，且右边有m位0，取反加1后，从右到左m个0，第m+1位机器左边全是1，这样x&（-x）得到的就是x
• x为偶数且不是2的m次方，得到$2^k$

int lowbit(int x)
{
    return x&(-x);
}

2.单点更新

void update(int x,int y,int n)
{
    while(x<=n)
    {
        c[x]+=y;
        x+=lowbit(x);
    }
}

3.区间查询

int getsum(int x)//对1~x的区间求和
{
    int res=0;
    while(x>0)
    {
        res+=c[x];
        x-=lowbit(x);
    }
    return res;
}

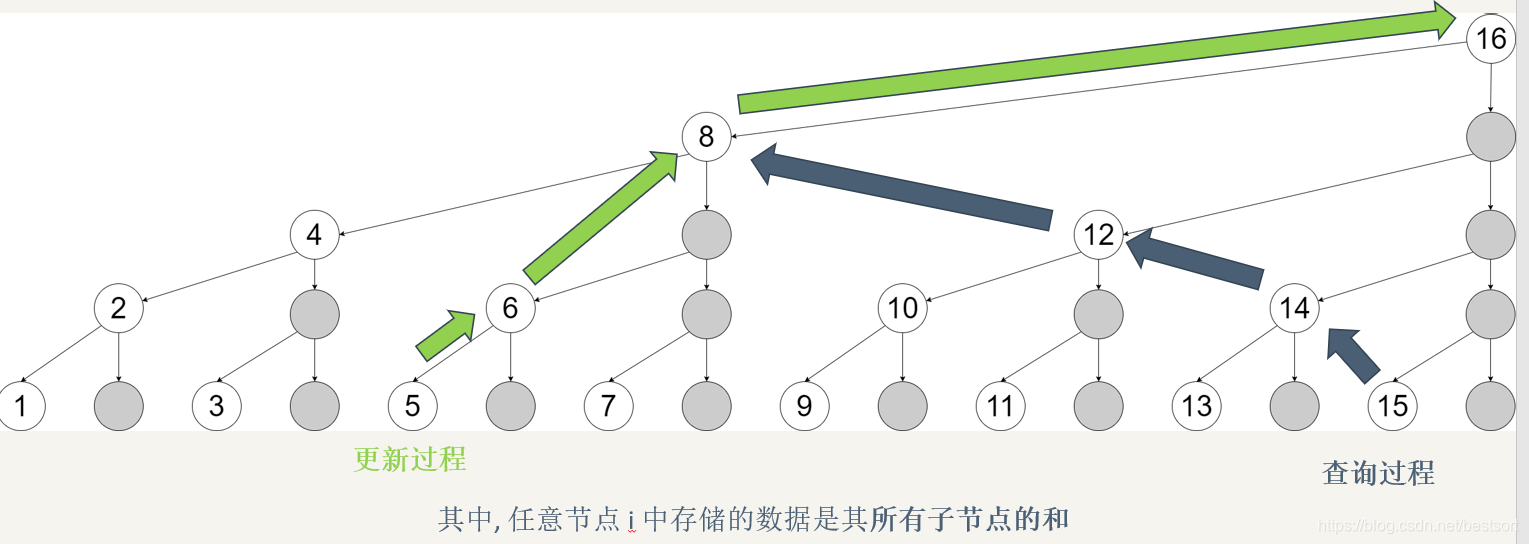
4.配图