数据结构总结

  • hash表：

散列表（Hash table，也叫哈希表），是根据关键码值 (Key value) ⽽直接进⾏访问的数据结构。 也就是说，它通过把关键码值映射到表中⼀个位置来访问记录， 以加快查找的速度。 这个映射函数叫做散列函数，存放记录的数组叫做散列表。

    • 哈希冲突

          哈希冲突是无可避免的，若想避免，必须新开空间，会导致空间增大

既然无法避免，就只能尽量减少冲突带来的损失，而一个好的哈希函数需要有以下特点：

 

　　1.尽量使关键字对应的记录均匀分配在哈希表里面

        2.关键字极小的变化可以引起哈希值极大的变化。

1 unsigned long hash(const char* key){
2     unsigned long hash=0;
3     for(int i=0;i<strlen(key);i++){
4         hash = hash*33+str[i];
5     }  
6     return hash;
7 }

 

    •  哈希冲突的解决办法

      1.开发定址法

      　　如果遇到冲突的时候怎么办呢？就找hash表剩下空余的空间，找到空余的空间然后插入。

                    2.链地址法

                       链地址法的原理时如果遇到冲突，他就会在原地址新建一个空间，然后以链表结点的形式插入到该空间

  • 并查集

      在一些有 N 个元素的集合应用问题中，我们通常是在开始时让 每个元素构成一个单元素的集合 然后按一定顺序将属于同一组的元素所在的集合合并，其间要反 复查找一个元素在哪个集合中 这一类问题数据量极大，若用正常的数据结构来描述的话，计算 机无法承受 只能采用一种全新的抽象的特殊数据结构——并查集来描述

    • 初始化 把每个点所在集合初始化为其自身 通常来说，这个步骤在每次使用该数据结构时只需要执一 次，无论何种实现形式，时间复杂度均为 O(n)
    •  查找 查找元素所在的集合，即根节点
    •  合并 将两个元素所在的集合合并为一个集合 通常来说，合并之前，应先判断两个元素是否属于同一集 合，这可用上面的“查找”操作实现
    • 路径压缩优化：
1 int find(int x) {
2     if (x != f[x]) f[x] = find(f[x]);
3     return f[x];
4 }
  • 线段树

线段树，是一种二叉搜索树。它将一段区间划分为若干单位区间，每一个节点都储存着一个区间。

线段树的每一个节点都储存着一段区间[L…R]的信息，其中叶子节点L=R。它的大致思想是：将一段大区间平均地划分成2个小区间，每一个小区间都再平均分成2个更小区间……以此类推，直到每一个区间的L等于R（这样这个区间仅包含一个节点的信息，无法被划分）。通过对这些区间进行修改、查询，来实现对大区间的修改、查询。

这样一来，每一次修改、查询的时间复杂度都只为O(log2n)

    • 初始化
 1 void build(int k,int l,int r)
 2 {
 3     a[k].l=l,a[k].r=r;
 4     if(l==r)//递归到叶节点
 5     {
 6         a[k].sum=number[l];//其中number数组为给定的初值
 7         return;
 8     }
 9     int mid=(l+r)/2;//计算左右子节点的边界
10     build(k*2,l,mid);//递归到左儿子
11     build(k*2+1,mid+1,r);//递归到右儿子
12     update(k);//记得要用左右子区间的值更新该区间的值
13 }
    • 单点修改
1 void change(int k,int x,int y)
2 {
3     if(a[k].l==a[k].r){a[k].sum=y;return;}
4     
5     int mid=(a[k].l+a[k].r)/2;//计算下一层子区间的左右边界
6     if(x<=mid) change(k*2,x,y);//递归到左儿子
7     else change(k*2+1,x,y);//递归到右儿子
8     update(k);
9 }
    • 区间修改

区间修改大体可以分为两步：

  1. 找到区间中全部都是要修改的点的线段树中的区间
  2. 修改这一段区间的所有点
    • 懒惰标记

标记的含义：本区间已经被更新过了，但是子区间却没有被更新过，被更新的信息是什么

我们区间修改时可以偷一下懒，先修改当前节点，然后直接把信息挂在节点上就可以了

下面是区间+x的代码：

 

void changeSegment(int k,int l,int r,int x)
//当前到了编号为k的节点，要把[l..r]区间中的所有元素的值+x
{
    if(a[k].l==l&&a[k].r==r)//如果找到了全部元素都要被修改的区间
    {
        a[k].sum+=(r-l+1)*x;
        //更新该区间的sum
        a[k].lazy+=x;return;
        //懒惰标记叠加
    }
    int mid=(a[k].l+a[k].r)/2;
    if(r<=mid) changeSegment(k*2,l,r,x);
    //如果被修改区间完全在左区间
    else if(l>mid) changeSegment(k*2+1,l,r,x);
    //如果被修改区间完全在右区间
    else changeSegment(k*2,l,mid,x),changeSegment(k*2+1,mid+1,r,x);
    //如果都不在，就要把修改区间分解成两块，分别往左右区间递归
    update(k);｝

 

 

 1 void pushdown(int k)//将点k的懒惰标记下传
 2 {
 3     if(a[k].l==a[k].r){a[k].lazy=0;return;}
 4     //如果节点k已经是叶节点了，没有子节点，那么标记就不用下传，直接删除就可以了
 5     a[k*2].sum+=(a[k*2].r-a[k*2].l+1)*a[k].lazy;
 6     a[k*2+1].sum+=(a[k*2+1].r-a[k*2+1].l+1)*a[k].lazy;
 7     //给k的子节点重新赋值
 8     a[k*2].lazy+=a[k].lazy;
 9     a[k*2+1].lazy+=a[k].lazy;
10     //下传点k的标记
11     a[k].lazy=0;//记得清空点k的标记
12 }

 

    • 区间查询
 1 int query(int k,int l,int r)
 2 
 3 {
 4     if(a[k].lazy) pushdown(k);
 5     if(a[k].l==l&&a[k].r==r) return a[k].sum;
 6     //如果当前区间就是询问区间，完全重合，那么显然可以直接返回
 7     int mid=(a[k].l+a[k].r)/2;
 8     if(r<=mid) return query(k*2,l,r);
 9     //如果询问区间包含在左子区间中
10     if(l>mid) return query(k*2+1,l,r);
11     //如果询问区间包含在右子区间中
12     return query(k*2,l,mid)+query(k*2+1,mid+1,r);
13     //如果询问区间跨越两个子区间
14 }
  •  树状数组

 

C[i]代表 子树的叶子结点的权值之和
如图可以知道
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
可以发现  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）
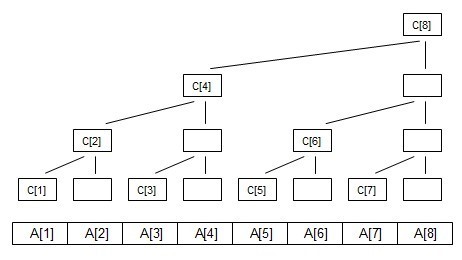
    • lowbit

lowbit(x) 其实就是取出x的最低位1  换言之  lowbit(x)=2^k 

int lowbit(int t)
{
return t&(-t);
}

 

    •  区间查询
举个例子 i=7;
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;   前i项和
C[4]=A[1]+A[2]+A[3]+A[4];   C[6]=A[5]+A[6];   C[7]=A[7];
可以推出:   sum[7]=C[4]+C[6]+C[7];
序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];
1 int getsum(int x)
2 {
3 int ans=0;
4 for(int i=x;i>0;i-=lowbit(i))
5 ans+=C[i];
6 return ans；
7 }

 

    • 单点更新

可以发现 更新过程是查询过程的逆过程

1 void add(int x,int y)
2 {
3 for(int i=x;i<=n;i+=lowbit(i))
4 tree[i]+=y;
5 }
  •  分块（思想：大段维护，局部朴素）

同样是类似于上面线段树和树状数组得问题

将数列分为若干个长度不超过sqrt（n）（向下取整）得段

另：sum和add数组分别表示第i段的区间和与增量标记

    • 区间修改

若lr处于同一段，则朴素更新

否则，将其中间的段add+=k（更新值）

然后剩下的朴素更新

    • 区间询问

同上：分类讨论

同一段，则原始值加上更新值

否则，将中间段累加，然后其余朴素累加

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<cmath>
 6 using namespace std;
 7 long long a[100010], sum[100010], add[100010];
 8 int L[100010], R[100010];
 9 int pos[100010];
10 int n, m, t;
11 
12 void change(int l, int r, long long d) {
13     int p = pos[l], q = pos[r];
14     if (p == q) {
15         for (int i = l; i <= r; i++) a[i] += d;
16         sum[p] += d*(r - l + 1);
17     }
18     else {
19         for (int i = p + 1; i <= q - 1; i++) add[i] += d;
20         for (int i = l; i <= R[p]; i++) a[i] += d;
21         sum[p] += d*(R[p] - l + 1);
22         for (int i = L[q]; i <= r; i++) a[i] += d;
23         sum[q] += d*(r - L[q] + 1);
24     }
25 }
26 
27 long long ask(int l, int r) {
28     int p = pos[l], q = pos[r];
29     long long ans = 0;
30     if (p == q) {
31         for (int i = l; i <= r; i++) ans += a[i];
32         ans += add[p] * (r - l + 1);
33     }
34     else {
35         for (int i = p + 1; i <= q - 1; i++)
36             ans += sum[i] + add[i] * (R[i] - L[i] + 1);
37         for (int i = l; i <= R[p]; i++) ans += a[i];
38         ans += add[p] * (R[p] - l + 1);
39         for (int i = L[q]; i <= r; i++) ans += a[i];
40         ans += add[q] * (r - L[q] + 1);
41     }
42     return ans;
43 }
44 
45 int main() {
46     cin >> n >> m;
47     for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
49     t = sqrt(n*1.0);
50     for (int i = 1; i <= t; i++) {
51         L[i] = (i - 1)*sqrt(n*1.0) + 1;
52         R[i] = i*sqrt(n*1.0);
53     }
54     if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
55 
56     for (int i = 1; i <= t; i++)
57         for (int j = L[i]; j <= R[i]; j++) {
58             pos[j] = i;
59             sum[i] += a[j];
60         }
61     while (m--) {
62         char op[3];
63         int l, r, d;
64         scanf("%s%d%d", op, &l, &r);
65         if (op[0] == 'C') {
66             scanf("%d", &d);
67             change(l, r, d);
68         }
69         else printf("%lld\n", ask(l, r));
70     }
71 }
  • 可持久化线段树

什么是可持久化线段树？

可持久化线段树最大的特点是：可以访问历史版本。

那么如何实现这样的一棵线段树呢？

想象一棵普通的线段树，我们要对它进行单点修改，需要修改logn个点。每次修改的时候，我们丝毫不修改原来的节点，而是在它旁边新建一个节点，把原来节点的信息（如左右儿子编号、区间和等）复制到新节点上，并对新节点进行修改。

那么如何查询历史版本呢？只需记录每一次修改对应的新根节点编号（根据上面描述的操作，根节点每次一定会新建一个的），每次询问从对应的根节点往下查询就好了。

 创建：

 

 1 struct SegmentTree {
 2     int lc, rc; 
 3     int dat;
 4 } tree[MAX_MLOGN];
 5 int tot, root[MAX_M]; 
 6 int n, a[MAX_N];
 7 
 8 int build(int l, int r) {
 9     int p = ++tot;
10     if (l == r) { tree[p].dat = a[l]; return p; }
11     int mid = (l + r) >> 1;
12     tree[p].lc = build(l, mid);
13     tree[p].rc = build(mid + 1, r);
14     tree[p].dat = max(tree[tree[p].lc].dat, tree[tree[p].rc].dat);
15     return p;
16 }
17 //在main中 
18 root[0] = build(1, n);

 

 单点修改

 

 1 int insert(int now, int l, int r, int x, int val) {
 2     int p = ++tot;
 3     tree[p] = tree[now]; 
 4     if (l == r) {
 5         tree[p].dat = val; 
 6         return p;
 7     }
 8     int mid = (l + r) >> 1;
 9     if (x <= mid) 
10 tree[p].lc = insert(tree[now].lc, l, mid, x, val);
11     else 
12 tree[p].rc = insert(tree[now].rc, mid + 1, r, x, val);
13     tree[p].dat = max(tree[tree[p].lc].dat, tree[tree[p].rc].dat);
14     return p;
15 }
16 // 在main中
17 root[i] = insert(root[i - 1], 1, n, x, val);

 

 

 

posted @ 2020-04-09 20:48  γδζ弱い  阅读(184)  评论(1)  编辑  收藏  举报