双重汉诺塔(白银-->黄金-->钻石)
汉诺塔作为递归经典例题为人熟知,在此介绍双重汉诺塔问题(《具体数学:计算机科学基础(第2版)》中的一道课后习题),结合数学逻辑推理和代码实现做一个小小总结,加入了一些自己对此的理解,主要参考资料来自贝神算法培训的课件(贝神yyds!!!)
1.经典汉诺塔回顾
1.1问题引入
问题来源:汉诺塔来源于印度传说的一个故事,上帝创造世界时作了三根金刚石柱子,在一根柱子上从上往下从小到大顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一回只能移动一个圆盘,只能移动在最顶端的圆盘。有预言说,这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。恩,当然这个传说并不可信,如今汉诺塔更多的是作为一个玩具存在。
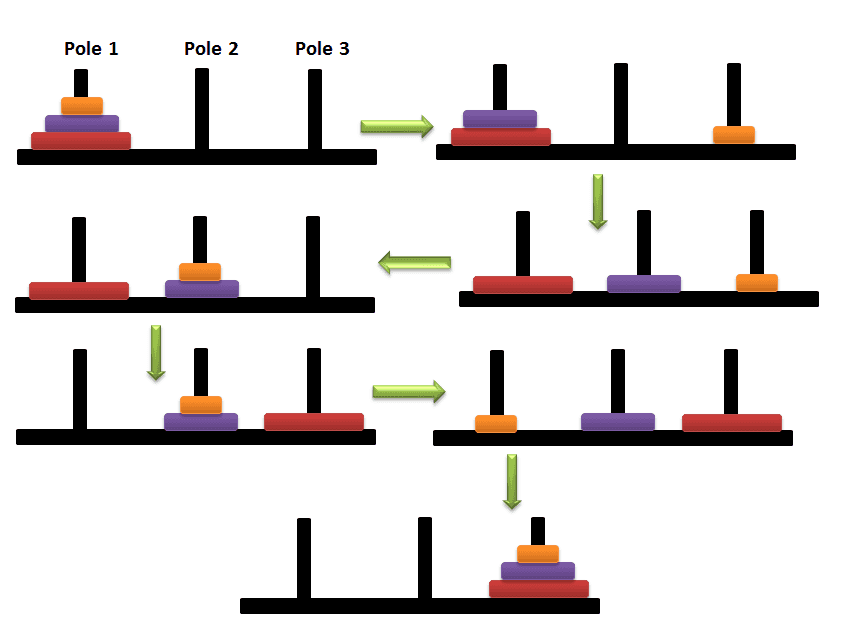
现在有n个圆盘从上往下从小到大叠在第一根柱子上,要把这些圆盘全部移动到第三根柱子要怎么移动呢?请找出需要步骤数最少的方案。
首先我们分析题目给出的的条件:
1.在小圆盘上不能放大圆盘。
2.一次只能移动一个在最顶端圆盘。
联系递归的要点:
1、明确递归终止条件(边界); 2、给出递归终止时的处理办法; 3、提取重复的逻辑,缩小问题规模。
递归就是有去(递去)有回(归来),如下图所示。“有去”是指:递归问题必须可以分解为若干个规模较小,与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决,就像上面例子中的钥匙可以打开后面所有门上的锁一样;“有回”是指 : 这些问题的演化过程是一个从大到小,由近及远的过程,并且会有一个明确的终点(临界点),一旦到达了这个临界点,就不用再往更小、更远的地方走下去。最后,从这个临界点开始,原路返回到原点,原问题解决。
首先我们考虑最简单的情况,再推导至n个盘子
正面思考这个问题比较复杂,但我们逆推,将问题转化为第n个和n-1个盘子的模型
那么我们把n个盘子从A柱移动至C柱的问题可以表示为:Hanio(n,A,B,C):
| 2个盘子 | 3个盘子 | n个盘子 |
|---|---|---|
| 第一步:将1个盘子从A柱移动至B柱(借助C柱为过渡柱) | 第一步:将2个盘子从A柱移动至B柱(借助C柱为过渡柱) | 第一步:将n-1个盘子从A柱移动至B柱(借助C柱为过渡柱) |
| 第二步:将A柱底下的盘子移动至C柱 | 第二步:将A柱底下最大的盘子移动至C柱 | 第二步:将A柱底下最大的盘子移动至C柱 |
| 第三步:将B柱的1个盘子移至C柱(借助A柱为过渡柱) | 第三步:将B柱的2个盘子移至C柱(借助A柱为过渡柱) | 第三步:将B柱的n-1个盘子移至C柱(借助A柱为过渡柱) |
1.2代码实现
1.3
总步数的计算(一个简单的数列计算)
经典汉诺塔有n个圆盘

2.双重汉诺塔--白银
2.1双重河内塔包含 2n 个圆盘,它们有 n 种不同的尺寸,每一种尺寸的圆盘有两个。如通常那样,要求每次只能移动一个圆盘,且不能把较大的圆盘放在较小的圆盘上面。
a.如果相同尺寸的圆盘是相互不可区分的,要把一个双重塔从一根桩柱移动到另一根桩柱需要移动多少次?
模仿上述思路
2*3个盘子
第一步:将2(3-1)个盘子从A柱移动至B柱(借助C柱为过渡柱)
第二步:将A柱底下的2个盘子移动至C柱
第三步:将B柱的2(3-1)个盘子移至C柱(借助A柱为过渡柱)
……
2n个盘子
那么我们把n个盘子从A柱移动至C柱的问题可以表示为: Hanio(n,A,B,C):
该问题可以分解成以下子问题: 第一步:将2(n-1)个盘子从A柱移动至B柱(借助C柱为过渡柱)
第二步:将A柱底下2个盘子移动至C柱
第三步:将B柱的2(n-1)个盘子移至C柱(借助A柱为过渡柱)
void Hanio(int n,char spos,char tpos,char epos){
if(n==1){
Move(n,spos,epos);
Move(n,spos,epos);
}
else{
Hanio(n-1,spos,epos,tpos);
Move(n,spos,epos);
Move(n,spos,epos);
Hanio(n-1,tpos,spos,epos);
}
}
3.双重汉诺塔--黄金
3.1*思考
双重河内塔包含 2n 个圆盘,它们有 n 种不同的尺寸,每一种尺寸的圆盘有两个。如通常那样,要求每次只能移动一个圆盘,且不能把较大的圆盘放在较小的圆盘上面。* b 如果在最后的排列中要把所有同样尺寸的圆盘恢复成原来的从上到下的次序,需要移动多少次

这个如何恢复顺序的问题一开始显得很难下手,但是我们依旧可以模仿上述思路
2*2个盘子
1.先将1-2圆盘挪到C柱
(为了简化问题,先不考虑它们的上下顺序是否改变
2.将3挪到B柱
3.将1-2号圆盘挪到B柱
4.将4移到C柱
5.将1-2号圆盘挪到A柱
6.将3挪到C柱 7.将1~2圆盘挪到C柱
……
2n个盘子
1.先将1~(2n-2)圆盘挪到C柱
2.将2n-1挪到B柱
3.将1~(2n-2)圆盘挪到B柱
4.将2n移到C柱
5.将1~(2n-2)圆盘挪到A柱
6.将2n-1挪到C柱
7.将1~(2n-2)圆盘挪到C柱 中间有四次An操作(函数Ahanoi)(即为将1~(2n-2)圆盘整体挪到C柱)
3.2难点
因为顺序要和初始的一样,第2n号圆盘应该,被放在第C柱的最低端然后再放上2n-1号盘子,最后再将1~(2n-2)号盘子全部移到C柱上。 但是我们怎么确定,移动1~(2n-2)号盘子就是顺序的呢?
因为执行一次An-1操作后只有最下面两个盘子的顺序会互换。则执行偶数倍次数的An-1操作后顺序不变。因为An中需要执行四次An-1操作,故1~(2n-2)个圆盘顺序不改变。
3.3详细证明
这个正证明可能有些难理解,建议画一画这个步骤实践一下。
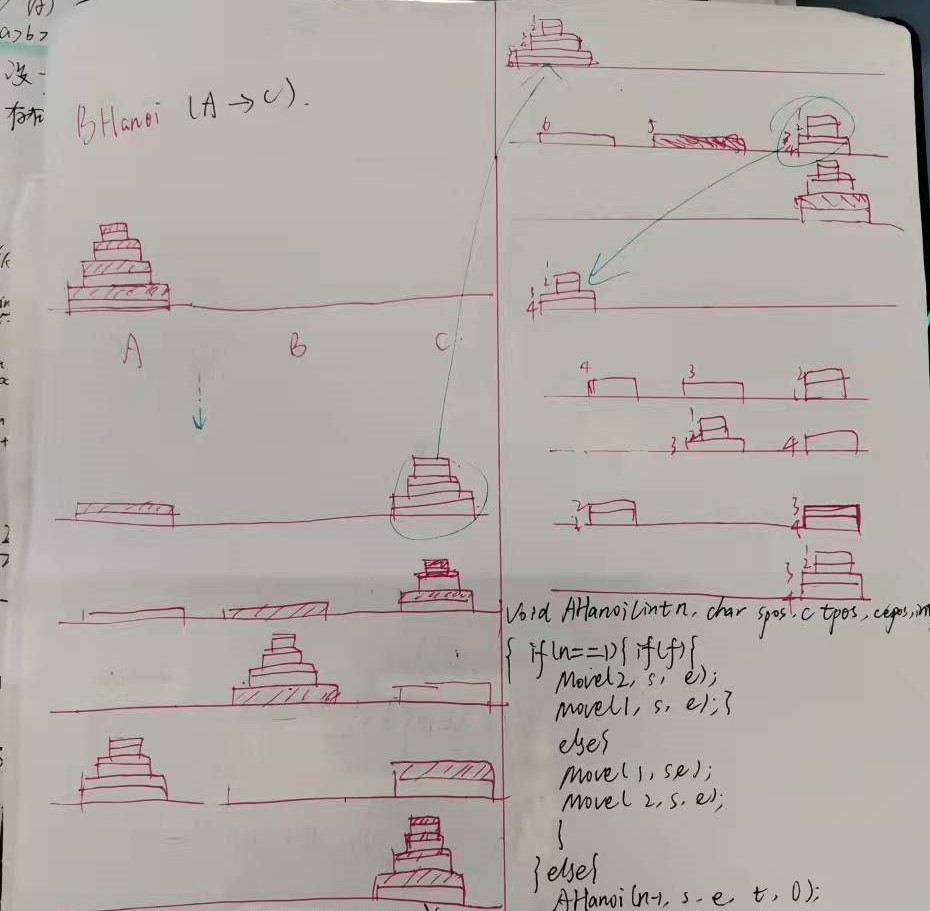


附上我一开始怎么都不能理解这个过程画的很多蛋糕(bushi)大家不懂的话也可以多画图去理解

4.双重汉诺塔--钻石
4.1思考
双重河内塔包含 2n 个圆盘,它们有 n 种不同的尺寸,每一种尺寸的圆盘有两个。如通常那样,要求每次只能移动一个圆盘,且不能把较大的圆盘放在较小的圆盘上面。
b 如果在最后的排列中要把所有同样尺寸的圆盘恢复成原来的从上到下的次序,需要移动多少次?
在上一题的基础上,编写一个中间输出区分2k-1和2k圆盘的程序。(即输出1-2n号盘子的编号
首先我们已经证明,AHanio函数执行后不会改变2(n-1)个盘子的顺序,故我们只需处理第2n和2n-1个盘子的顺序逆序问题。
考虑用f=0或1表示这两个盘子的正逆序状态。
4.2代码实现
#include <bits/stdc++.h>
using namespace std;
int n, step;
void Move(int id, char sPos, char ePos) {
step ++ ;
printf("第%d步:将%d号圆盘从%c柱移动到%c\n", step, id, sPos, ePos);
}
void AHanoi(int n, char sPos, char tPos, char ePos, bool f)
// f == 0 代表当前(未移动)2n-1 2n 正序
// f == 1 代表逆序
// 1~2n-2全部都是顺序,
{
if(n == 1) {
if(!f) { // 0 = false 非零 =true
//顺序
Move(1, sPos, ePos);
Move(2, sPos, ePos);
} else {
Move(2, sPos, ePos);
Move(1, sPos, ePos);
}
} else {
AHanoi(n - 1,sPos, ePos, tPos, 0);
if(!f) {
Move(2 * n - 1, sPos, ePos);
Move(2 * n, sPos, ePos);
} else {
Move(2 * n, sPos, ePos);
Move(2 * n - 1, sPos, ePos);
}
AHanoi(n - 1,tPos, sPos, ePos, 1);//1
}
}
void solve(int n, char sPos, char tPos, char ePos) {
if(n == 1) {
Move(1, sPos, tPos);
Move(2, sPos, ePos);
Move(1, tPos, ePos);
} else {
AHanoi(n - 1, sPos, tPos, ePos, 0);
Move(2 * n - 1, sPos, tPos);
AHanoi(n - 1, ePos, sPos, tPos, 1);
Move(2 * n, sPos, ePos);
AHanoi(n - 1, tPos, ePos, sPos, 0);
Move(2 * n - 1, tPos, ePos);
AHanoi(n - 1, sPos, tPos, ePos, 1);
}
}
int main() {
cin >> n;
solve(n, 'A', 'B', 'C');
cout << "总得步数为:" << step << endl;
}
5多柱汉诺塔(拓展)
引用一篇大牛的博客,有兴趣的同学可以继续看,难度较大。
**1.** 三柱汉诺塔**
三柱汉诺塔是经典的汉诺塔问题,在算法设计中是递归算法的典型问题。其算法是这样的: 首先把A 柱上面的n- 1 个碟子通过C 柱移到B 柱上【T(n-1)步】,然后把A 柱剩下的一个碟子移到C 柱上【1步】, 最后把B 柱上所有的碟子通过A 柱移到C 柱上【T(n-1)步】。很容易得到算法的递归方程为:T(n)=2*T(n-1)+1,因此,不难算出步数是T(n)=2^n-1。对于三柱汉诺塔的算法的正确性自然是毫无争议的,我们需要的是从三柱汉诺塔的设计中引申出多柱汉诺塔的设计方法。
**2.** 四柱汉诺塔**
四柱汉诺塔并不是仅仅是多了一根柱子那么简单,所以我们先尝试从正常的思维出发来探究如何使移动步数最少。
首先我们会想到,三柱汉诺塔需要借助另一个柱子存放前n-1个盘子,再把第n个盘子移动到目的位置。顺其自然的,四柱汉诺塔由于多了一个柱子,所以移动起来就更方便了,我们可以多留下一个盘子n-2,而不让它借位到其他柱子直接移动到目的位置。这样我们就得出算法的基本流程:
(1) 从A借助C、D将 n-2个盘子移动到B上。
(2) 将n-2移动到C上。
(3) 将n-1移动到D上。
(4) 将n-2移动到D上。
(5) 从B借助A、C将 n-2个盘子移动到D上。
另外,这么设计是符合正常思维原则的。以为随着柱子的个数增多,我们希望每次移动的时候盘子尽可能不发生折叠,也就是说我们希望除了需要借助存放n-2个盘子的柱子。那么剩下的两个柱子可以允许至多两个盘子不发生折叠就能直接移动到目的位置,这样才使得移动起来比较方便,步骤也会比较少。但事实真的是如此吗?(考虑到这里涉及的思维深度,不继续展开,有兴趣的同学可以看下方原博客)
参考博客:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号