两个有序数组的第 K 小乘积(第k小转化为二分)
这种题一个套路问题
https://www.cnblogs.com/lipu123/p/15435169.html
几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第 k 小的数字吗?
乘法表是大小为\(m x n\)的一个整数矩阵,其中\(mat[i][j] == i * j\)(下标从 1 开始)。
给你三个整数\(m、n 和 k\),请你在大小为\(m x n\)的乘法表中,找出并返回第\(k\)小的数字。
示例 1:
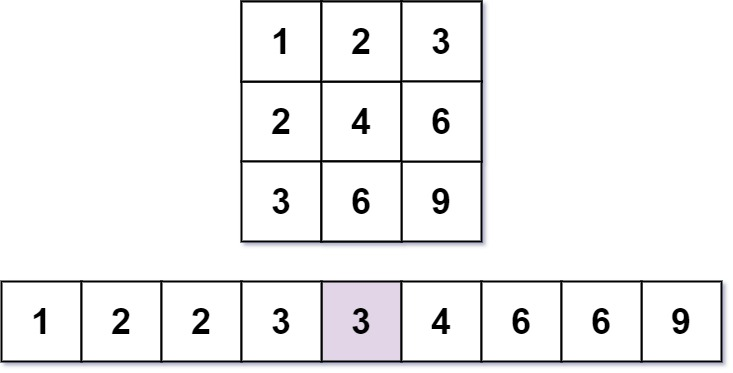
输入:m = 3, n = 3, k = 5
输出:3
解释:第 5 小的数字是 3 。
示例 2:
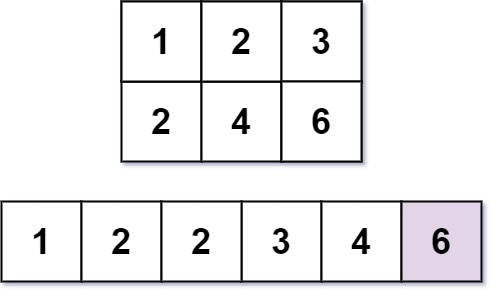
输入:m = 2, n = 3, k = 6
输出:6
解释:第 6 小的数字是 6 。
提示:
\(1 <= m, n <= 3 * 10^4\)
\(1 <= k <= m * n\)
这个题直接求得话,会超时,因为n和m都比较大。这种求个数得题可以转化为二分。然后judge得时候就是求有多少个数小于mid,然后求个数大于k得最小的一个就行。这也转化成了大于k的最小值,也是一个二分。
然后就是求有多少数字不超过 \(x\)。
我们可以遍历乘法表的每一行,对于乘法表的第 \(i\) 行,其数字均为 \(i\) 的倍数,因此不超过 \(x\) 的数字有 \(\min(\Big\lfloor\dfrac{x}{i}\Big\rfloor,n)\)个,所以整个乘法表不超过 \(x\) 的数字个数为
由于$ i≤\lfloor\dfrac{x}{i}\rfloor$时 \(\lfloor\dfrac{x}{i}\rfloor ≥n\),上式可化简为
由于 \(x\) 越大上式越大,\(x\) 越小上式越小,因此我们可以二分 \(x\) 找到答案,二分的初始边界为乘法表的元素范围,即 \([1,mn]\)。
class Solution {
public:
int findKthNumber(int m, int n, int k) {
int l=1,r=m*n,ans=1;
while(r>=l){
int mid=(l+r)/2;
int cnt=mid/n*n;
for(int i=mid/n+1;i<=m;i++){
cnt+=mid/i;
}
if(cnt>=k){
ans=mid;
r=mid-1;
}
else{
l=mid+1;
}
}
return ans;
}
};
两个有序数组的第 K 小乘积&两个有序数组的第 K 大乘积
https://leetcode.cn/problems/kth-smallest-product-of-two-sorted-arrays/description/
https://codefun2000.com/p/P1052
第一个是第k小乘积,第二个是第k大乘积
通过二分查找第 \(k\) 小的乘积 \(p\),每次判定时枚举 nums1 中的数 \(a\),通过二分再次判断 nums2 中有几个数 bbb 满足 \(ab \le p\)。注意需要对 a>0,a<0 和a = 0三种情况分别讨论。复杂度 \(\mathcal{O}(n\log n\log A)\)。
#include<iostream>
#include<algorithm>
using namespace std;
//article
typedef long long ll;
const int maxn=5e5+100;
ll a[maxn],b[maxn];
ll n,m,k;
ll get(ll mid){//小于等于mid的个数
ll sum=0;
for(int i=1;i<=n;i++){
ll x=a[i];
if(x<0){
ll L=1,R=m,ans=m+1;//大->小
while(R>=L){
ll mid2=(R+L)/2;
if(x*b[mid2]<=mid){
R=mid2-1;
ans=mid2;
}
else{
L=mid2+1;
}
}
sum+=(m-ans+1);
}
else if(x==0){
if(mid>=0){
sum+=m;
}
}else if(x>0){
ll L=1,R=m,ans=0;//小->大
while(R>=L){
int mid2=(R+L)/2;
if(x*b[mid2]<=mid){
L=mid2+1;
ans=mid2;
}
else{
R=mid2-1;
}
}
sum+=ans;
}
}
return sum;
}
int main(){
//第k小
cin>>n>>m>>k;
//k=m*n-k+1;去掉这个注释就是第k大
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=m;i++)
cin>>b[i];
sort(b+1,b+m+1);
ll l=-1e13,r=1e13,ans=0;
while(r>=l){
ll mid=(l+r)/2;
ll sum=get(mid);
if(sum>=k){
ans=mid;
r=mid-1;
}else{
l=mid+1;
}
}
cout<<ans<<endl;
}
/*
3 4 5
5 -4 0
3 4 5 1
9
-20 -16 -12 -4 0 0 0 0 5 15 20 25
*/
/*
2 2 1
-100000 100000
-100000 100000
-10000000000 -10000000000 10000000000 10000000000
*/
typedef long long ll;
const int maxn=1e5+100;
class Solution {
int a[maxn],b[maxn],n,m;
public:
ll get(ll mid){//小于等于mid的个数
ll sum=0;
for(int i=1;i<=n;i++){
ll x=a[i];
if(x<0){
ll L=1,R=m,ans=m+1;//大->小
while(R>=L){
ll mid2=(R+L)/2;
if(x*b[mid2]<=mid){
R=mid2-1;
ans=mid2;
}
else{
L=mid2+1;
}
}
sum+=(m-ans+1);
}
else if(x==0){
if(mid>=0){
sum+=m;
}
}else if(x>0){
ll L=1,R=m,ans=0;//小->大
while(R>=L){
int mid2=(R+L)/2;
if(x*b[mid2]<=mid){
L=mid2+1;
ans=mid2;
}
else{
R=mid2-1;
}
}
sum+=ans;
}
}
return sum;
}
long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
n=nums1.size();
m=nums2.size();
for(int i=1;i<=n;i++){
a[i]=nums1[i-1];
}
for(int i=1;i<=m;i++){
b[i]=nums2[i-1];
}
sort(b+1,b+m+1);
ll l=-1e13,r=1e13,ans;
while(r>=l){
ll mid=(l+r)/2;
ll sum=get(mid);
if(sum>k){
ans=mid;
r=mid-1;
}else if(sum==k){
ans=mid;
r=mid-1;
}else{
l=mid+1;
}
}
return ans;
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号