访问消失节点最小的时间(堆优化的dijkstra)
给你一个二维数组 edges 表示一个 n 个点的无向图,其中\(edges[i] = [u_i, v_i, length_i]\)表示节点\(u_i\)和节点\(v_i\)之间有一条需要 lengthi 单位时间通过的无向边。
同时给你一个数组\(disappear\),其中\(disappear[i]\)表示节点 i 从图中消失的时间点,在那一刻及以后,你无法再访问这个节点。
注意,图有可能一开始是不连通的,两个节点之间也可能有多条边。
请你返回数组\(answer\),\(answer[i]\) 表示从节点 0 到节点 i 需要的 最少 单位时间。如果从节点 0 出发 无法 到达节点\(i\),那么\(answer[i]\)为 -1 。
示例 1:
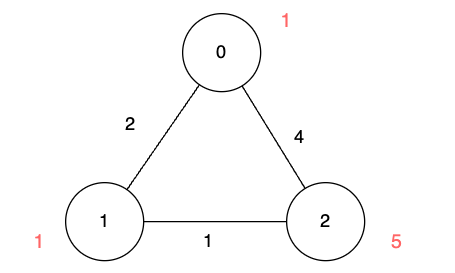
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]
输出:[0,-1,4]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
对于节点 1 ,我们需要至少 2 单位时间,通过 edges[0] 到达。但当我们到达的时候,它已经消失了,所以我们无法到达它。
对于节点 2 ,我们需要至少 4 单位时间,通过 edges[2] 到达。
示例 2:
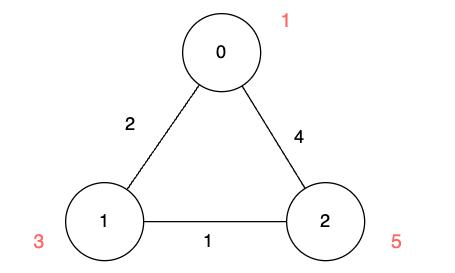
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]
输出:[0,2,3]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
对于节点 1 ,我们需要至少 2 单位时间,通过 edges[0] 到达。
对于节点 2 ,我们需要至少 3 单位时间,通过 edges[0] 和 edges[1] 到达。
示例 3:
输入:n = 2, edges = [[0,1,1]], disappear = [1,1]
输出:[0,-1]
解释:
当我们到达节点 1 的时候,它恰好消失,所以我们无法到达节点 1 。
提示:
\(1 <= n <= 5 * 10^4\)
\(0 <= edges.length <= 10^5\)
edges[i] == [ui, vi, lengthi]
0 <= ui, vi <= n - 1
\(1 <= lengthi <= 10^5\)
disappear.length == n
\(1 <= disappear[i] <= 10^5\)
class Solution {
public:
vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {
vector<pair<int, int>> e[n];
for (auto& ee : edges) {
int x = ee[0], y = ee[1], wt = ee[2];
e[x].emplace_back(y, wt);
e[y].emplace_back(x, wt);
}
vector<int>dis(n,0x3f3f3f3f);
dis[0]=0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> q;
q.emplace(0, 0);
vector<int>vis(n,0);
while(!q.empty()){
auto [x,u]=q.top();
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=0;i<e[u].size();i++){
auto [v,y]=e[u][i];
int new_dis=x+y;
if(new_dis<disappear[v]&&dis[v]>new_dis){
dis[v] = new_dis;
q.emplace(new_dis, v);
}
}
}
for(int i=0;i<dis.size();i++){
if(dis[i]==0x3f3f3f3f){
dis[i]=-1;
}
}
return dis;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号