leetcode中的并查集

省份数量

https://leetcode.cn/problems/number-of-provinces/description/
有$n$个城市，其中一些彼此相连，另一些没有相连。如果城市$a$与城市$b$直接相连，且城市$b$与城市$c$直接相连，那么城市$a$与城市$c$间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。
给你一个$n x n$的矩阵$isConnected$，其中$isConnected[i][j] = 1$表示第$i$个城市和第$j$个城市直接相连，而$isConnected[i][j] = 0$表示二者不直接相连。
返回矩阵中省份的数量。

示例 1：

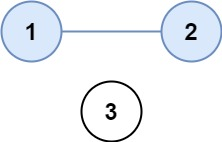
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

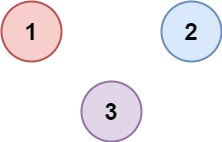
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：
1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

class Solution {
public:
    int pre[5000];
    int find(int x){
        if(pre[x]==x){
            return x;
        }
        return pre[x]=find(pre[x]);
    }
    void marge(int x,int y){
        int fx=find(x);
        int fy=find(y);
        if(fx!=fy){
            pre[fx]=fy;
        }
    }
    int findCircleNum(vector<vector<int>>& isConnected) {
        int n=isConnected.size();
        int m=isConnected[0].size();
        for(int i=0;i<=n;i++){
            pre[i]=i;
        }
        for(int i=1;i<=n;i++){
            for(int j=i+1;j<=n;j++){
                if(isConnected[i-1][j-1]==1){
                    marge(i,j);
                }
            }
        }
        int ans=0;
        for(int i=1;i<=n;i++){
            if(find(i)==i){
                ans++;
            }
        }
        return ans;
    }
};

冗余连接

https://leetcode.cn/problems/redundant-connection/
树可以看成是一个连通且无环的无向图。
给定往一棵$n$个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在$1$到$n $中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为$n$的二维数组$edges$，$edges[i] = [ai, bi]$ 表示图中在$ai$和$bi$之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着$n$个节点的树。如果有多个答案，则返回数组$edges$中最后出现的那个。

示例 1：

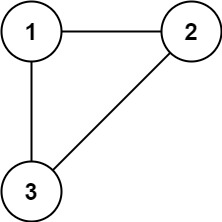
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

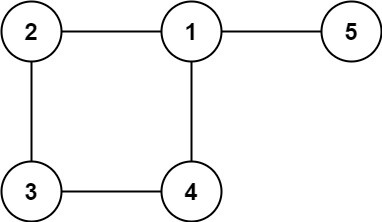
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

class Solution {
public:
    int pre[5000];
    int find(int x){
        if(pre[x]==x){
            return x;
        }
        return pre[x]=find(pre[x]);
    }
    void marge(int x,int y){
        int fx=find(x);
        int fy=find(y);
        if(fx!=fy){
            pre[fx]=fy;
        }
    }
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n=edges.size();
        for(int i=0;i<=n;i++){
            pre[i]=i;
        }
        vector<int> ans;
        for(int i=0;i<n;i++){
            int fx=find(edges[i][0]);
            int fy=find(edges[i][1]);
            if(fx==fy){
                ans.push_back(edges[i][0]);
                ans.push_back(edges[i][1]);
                break;
            }
            else{
                pre[fx]=fy;
            }
        }
        return ans;
    }
};

连通网络的操作次数

https://leetcode.cn/problems/number-of-operations-to-make-network-connected/description/
题目描述
用以太网线缆将$n$台计算机连接成一个网络，计算机的编号从$0$到$n-1$。线缆用connections表示，其中 $connections[i] = [a, b]$连接了计算机$a$和$b$。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线$connections$，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

示例 1：

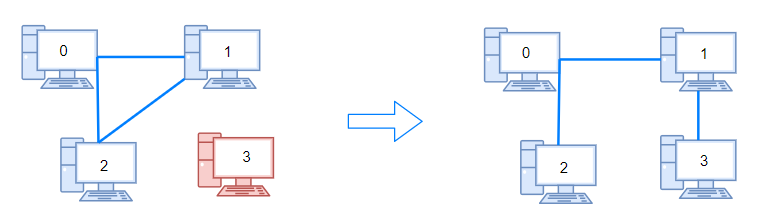
输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

示例 2：

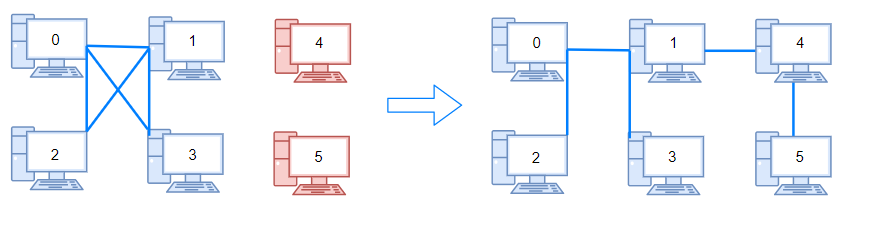
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

示例 3：
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]

输出：-1
解释：线缆数量不足。

示例 4：
输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]

输出：0

提示：
$1 <= n <= 10^5$
$1 <= connections.length <= min(n*(n-1)/2, 10^5)$
$connections[i].length == 2$
$0 <= connections[i][0], connections[i][1] < n$
$connections[i][0] != connections[i][1]$
没有重复的连接。
两台计算机不会通过多条线缆连接。

class Solution {
public:
    int pre[100100];
    int find(int x){
        if(pre[x]==x){
            return x;
        }
        return pre[x]=find(pre[x]);
    }
    void marge(int x,int y){
        int fx=find(x);
        int fy=find(y);
        if(fx!=fy){
            pre[fx]=fy;
        }
    }
    int makeConnected(int n, vector<vector<int>>& connections) {
        if (n - 1 > connections.size()) // 连通所有节点至少需要n-1条线缆, 少于n-1条线缆则无法连通所有节点，返回-1
            return -1;

        for(int i=0;i<=n;i++){
            pre[i]=i;
        }
        for(int i=0;i<connections.size();i++){
            marge(connections[i][0],connections[i][1]);
        }
        int ans=0;
        for(int i=0;i<n;i++){
            if(find(i)==i){
                ans++;
            }
        }
        return ans-1;
    }
};

最小体力消耗路径

你准备参加一场远足活动。给你一个二维$rows x columns$的地图$heights$，其中$heights[row][col]$表示格子$(row, col)$的高度。一开始你在最左上角的格子$(0, 0)$，且你希望去最右下角的格子$(rows-1, columns-1)$（注意下标从 0 开始编号）。你每次可以往上，下，左，右 四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小体力消耗值。

示例 1：

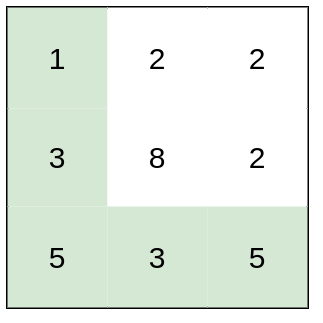
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

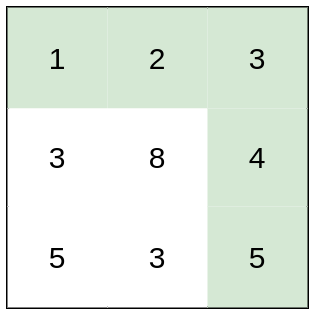
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

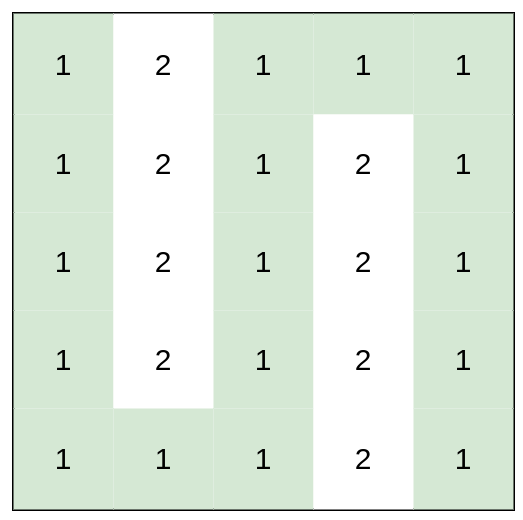
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
$1 <= heights[i][j] <= 10^6$

这个题可以用二分或者并查集

二分

二分就是先二分答案，然后再判断这个二分的答案可不可以

class Solution {
public:
    int dx[4]={0,0,-1,1};
    int dy[4]={-1,1,0,0};
    struct node{
        int x,y;
    };
    int minimumEffortPath(vector<vector<int>>& heights) {
        int n=heights.size();
        int m=heights[0].size();    
        int l=0,r=1e6,ans;
        while(r>=l){
            int mid=(l+r)/2;
            queue<node> q;
            q.push({0,0});
            vector<int> vis(n*m);
            vis[0]=1;
            while(!q.empty()){
                node now=q.front();
                q.pop();
                for(int i=0;i<4;i++){
                    int xx=now.x+dx[i];
                    int yy=now.y+dy[i];
                    if(xx>=0&&xx<n&&yy>=0&&yy<m&&!vis[xx*m+yy]&&abs(heights[now.x][now.y]-heights[xx][yy])<=mid){
                        q.push({xx, yy});
                        vis[xx * m + yy] = 1;
                    }
                }
                
            }
            if(vis[n*m-1]){
                ans=mid;
                r=mid-1;
            }
            else{
                l=mid+1;
            }
        } 
        return ans;  
    }
};

并查集

我们先将这$m \times n$个节点放入并查集中。
由于我们需要找到从左上角到右下角的最短路径，因此我们可以将图中的所有边按照权值从小到大进行排序，并依次加入并查集中。当我们加入一条权值为$x$的边之后，如果左上角和右下角从非连通状态变为连通状态，那么 $x$ 即为答案。

class Solution {
public:
    struct node{
        int dis,x,y;
    };
    int dx[2]={0,1};
    int dy[2]={1,0};
    int pre[200005];
    int find(int x){
        if(pre[x]==x){
            return pre[x];
        }
        return pre[x]=find(pre[x]);
    }
    void marge(int x,int y){
        int fx=find(x),fy=find(y);
        if(fx!=fy){
            pre[fx]=fy; 
        }
    }
    int minimumEffortPath(vector<vector<int>>& heights) {
        int n=heights.size(),m=heights[0].size();
        for(int i=0;i<=m*n;i++){
            pre[i]=i;
        }
        vector<node>edge;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                for(int k=0;k<2;k++){
                    int x=i+dx[k],y=j+dy[k];
                    if(x>=0&&x<n&&y>=0&&y<m){
                        edge.push_back({abs(heights[i][j]-heights[x][y]),i*m+j,x*m+y});    
                    }
                }
            }
        }
        sort(edge.begin(),edge.end(),[&](node a, node b){
            return a.dis<b.dis;
        });
        for(int i=0;i<edge.size();i++){
            node now=edge[i];
            marge(now.x,now.y);
            if(find(0)==find(m*n-1)){
                return now.dis;
            }
        }
        return 0;
    }
};

交换字符串中的元素

给你一个字符串$s$，以及该字符串中的一些「索引对」数组$pairs$，其中$pairs[i] = [a, b]$表示字符串中的两个索引（编号从 0 开始）。
你可以任意多次交换在$pairs$中任意一对索引处的字符。
返回在经过若干次交换后，$s$可以变成的按字典序最小的字符串。

示例 1:
输入：s = "dcab", pairs = [[0,3],[1,2]]
输出："bacd"
解释： 
交换 s[0] 和 s[3], s = "bcad"
交换 s[1] 和 s[2], s = "bacd"

示例 2：
输入：s = "dcab", pairs = [[0,3],[1,2],[0,2]]
输出："abcd"
解释：
交换 s[0] 和 s[3], s = "bcad"
交换 s[0] 和 s[2], s = "acbd"
交换 s[1] 和 s[2], s = "abcd"

示例 3：
输入：s = "cba", pairs = [[0,1],[1,2]]
输出："abc"
解释：
交换 s[0] 和 s[1], s = "bca"
交换 s[1] 和 s[2], s = "bac"
交换 s[0] 和 s[1], s = "abc"

提示：

$1 <= s.length <= 10^5$
$0 <= pairs.length <= 10^5$
$0 <= pairs[i][0], pairs[i][1] < s.length$
$s$ 中只含有小写英文字母

既然可以任意地交换通过「索引对」直接相连的字符，那么我们也任意地交换通过「索引对」间接相连的字符。我们利用这个性质将该字符串抽象：将每一个字符抽象为「点」，那么这些「索引对」即为「边」，我们只需要维护这个「图」的连通性即可。对于同属一个连通块（极大连通子图）内的字符，我们可以任意地交换它们。

这样我们的思路就很清晰了：利用并查集维护任意两点的连通性，将同属一个连通块内的点提取出来，直接排序后放置回其在字符串中的原位置即可。

这个是典型的并查集，就是将同一个根的进行排序，然后最后整合就行

class Solution {
public:
    int pre[100100];
    int find(int x){
        if(pre[x]==x){
            return pre[x];
        }
        return pre[x]=find(pre[x]);
    }
    string smallestStringWithSwaps(string s, vector<vector<int>>& pairs) {
        int n=s.size();
        for(int i=0;i<n;i++){
            pre[i]=i;
        }
        for(int i=0;i<pairs.size();i++){
            pre[find(pairs[i][0])]=find(pairs[i][1]);
        }
        vector<vector<char>>v(n);
        for(int i=0;i<n;i++){
            v[find(i)].push_back(s[i]);
        }
        string ans;
        for(int i=0;i<n;i++){
            sort(v[i].rbegin(),v[i].rend());//逆向排序
        }
        string res;
        for(int i=0;i<n;i++){
            res+=v[pre[i]].back();//倒着取
            v[pre[i]].pop_back();
        }
        return res;
    }
};

posted @ 2024-01-04 21:03 lipu123 阅读(60) 评论(0) 收藏举报

刷新页面返回顶部

lipu123