盛最多水的容器(双指针)

给定一个长度为$n$的整数数组$height$。有$n$条垂线，第$i$条线的两个端点是$(i,0)$和$(i,height[i])$。
找出其中的两条线，使得它们与$x$轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

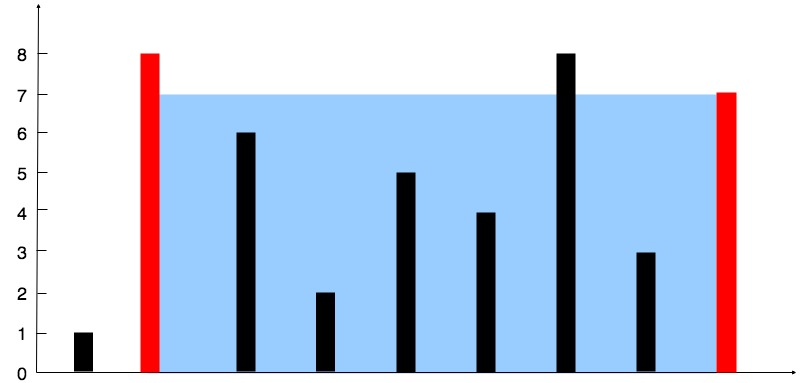
示例 1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
$2 <= n <= 10^5$
$0 <= height[i] <= 10^4$

这个题是典型的双指针问题，主要的问题就是这个指针怎么移动的问题。这个问题主要有这两个关键：

• 相同情况下两边距离越远越好
• 区域受限于较短边
  所以说我们一开始应该将指针置于两端，l=0,r=n-1。那该怎么移动指针呢，这个就利用第二个结论，区域受限于较短边，也就是先比较height[l]和height[r]的大小，如果height[l]>height[r],那么r--。如果height[l]<height[r],那么l++。
  其实就是每次固定较长的那条边，短边向内移动，然后判断面积是否有可能增大。

官方题解
代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n=height.size();
        int l=0,r=n-1,ma=0;
        while(r>l){
            ma=max(ma,min(height[l],height[r])*(r-l));
            if(height[r]>height[l]){
                l++;
            }
            else{
                r--;
            }
        }
        return ma;
    }
};