数论模板
试除法判定质数
bool is_prime(int x){
if(x<2) return false;
for(int i=2;i*i<=x;i++){
if(x%i==0){
return false;
}
}
return true;
}
筛素数
朴素筛法求素数(埃式筛)
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
线性筛法求素数(欧拉筛)
int prime[maxn],cnt;//prime[]存储所有素数
bool biaoji[maxn];//biaoji[x]存储是否筛掉
void get_prime(int n){
for(int i=2;i<=n;i++){
if(!biaoji[i]) prime[++cnt]=i;
for(int j=1;i*prime[j]<=n;j++){
biaoji[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
分解质因子
试除法分解质因数
bool divide(int x){
for(int i=2;i<=x/i;i++){
if(x%i==0){
int s=0;
while(s%i==0){
x/=i;
s++;
}
cout<<i<<" "<<s<<endl;
}
}
if(x>1){
cout<<x<<" "<<1<<endl;
}
}
素数分解质因子
void divide(int x){
for(int i=1;prime[i]*prime[i]<=x;i++){
int cnt=0;
while(x%prime[i]==0){
x/=prime[i];
cnt++;
}
if(cnt){
cout<<prime[i]<<" "<<cnt<<endl;
}
}
if(x!=1){
cout<<x<<" "<<1<<endl;
}
}
区间素数筛
做题的时候如果是多组查询,那么可以先把1~1e6的素数打表筛出来;
同时这个筛法不仅可以把素数的个数筛出来,也可以把区间素数和给求出来,以及每个素数是多少求出来
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e5+100;
#define MAX_L 1000007
#define MAX_SORT_B 1000007
typedef long long LL;
bool is_prime[MAX_L];
bool is_prime_small[MAX_SORT_B];
//对区间[a,b)内的整数执行筛法。isprime[i - a]=true <=> i是素数
void segment_sieve(LL a,LL b)
{
for(int i=0; (LL)i*i < b; i++)is_prime_small[i]=true;
for(int i=0; i<b-a; i++)is_prime[i]=true;
for(int i=2; (LL)i * i<b; i++)
{
if(is_prime_small[i])
{
for(int j=2*i; (LL)j * j < b; j += i)
{
is_prime_small[j]=false;//筛[2,sqrt(b))
}
for(LL j=max(2LL, (a+i-1)/i)*i ; j<b; j+=i) //(a+i-1)/i为[a,b)区间内的第一个数至少为i的多少倍.
{
is_prime[j - a] =false;//筛[a,b)
}
}
}
}
int main()
{
long long a,b;
while(~scanf("%lld %lld",&a,&b))
{
segment_sieve(a,b);
int cnt=0;
for(int j=0; j<b-a; j++)
{
if(is_prime[j])cnt++;
}
if(a==1)cnt--;
printf("%d\n",cnt);
}
return 0;
}
Min_25求1~n质数和
时间复杂度:\(\frac{O^{3/4}}{log(n)}\),复杂度比线性好多了,n=1e10时,大概是3e6的复杂度
const int N=1000010;
namespace Min25 {
int prime[N], id1[N], id2[N], flag[N], ncnt, m;
ll g[N], sum[N], a[N], T, n;
inline int ID(ll x) {
return x <= T ? id1[x] : id2[n / x];
}
inline ll calc(ll x) {
return x * (x + 1) / 2 - 1;
}
inline ll f(ll x) {
return x;
}
inline void init() {
//for(int i=0;i<=N;i++) prime[i]=id1[i]=id2[i]=flag[i]=g[i]=sum[i]=a[i]=0,ncnt=0,m=0;
ncnt=m=0;
T = sqrt(n + 0.5);
for (int i = 2; i <= T; i++) {
if (!flag[i]) prime[++ncnt] = i, sum[ncnt] = sum[ncnt - 1] + i;
for (int j = 1; j <= ncnt && i * prime[j] <= T; j++) {
flag[i * prime[j]] = 1;
if (i % prime[j] == 0) break;
}
}
for (ll l = 1; l <= n; l = n / (n / l) + 1) {
a[++m] = n / l;
if (a[m] <= T) id1[a[m]] = m; else id2[n / a[m]] = m;
g[m] = calc(a[m]);
}
for (int i = 1; i <= ncnt; i++)
for (int j = 1; j <= m && (ll)prime[i] * prime[i] <= a[j]; j++)
g[j] = g[j] - (ll)prime[i] * (g[ID(a[j] / prime[i])] - sum[i - 1]);
}
inline ll solve(ll x) {
if (x <= 1) return x;
return n = x, init(), g[ID(n)];
}
}
int main()
{
ll n;
cin >>n;
cout <<Min25::solve(n)<<endl;
}
试除法求约数(求一个数的所有因子)
vector<int> get_divisors(int x)
{
vector<int> res;//存放所有因子
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());//将所有因子从小到大进行排序
return res;
}
约数个数与约数之和
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
欧几里得算法(求GCD)
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
或者使用c++函数 __gcd();
求欧拉函数
1 ~ N 中与 N 互质的数的个数被称为欧拉函数,记为\(\phi(N)\);
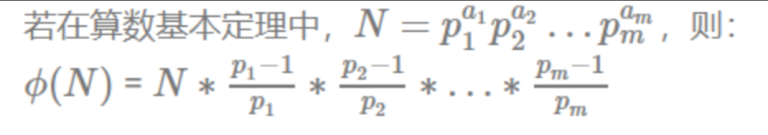
int phi(int x)
{
int res = x;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}
欧拉函数
筛法求欧拉函数
int primes[N], cnt; // primes[]存储所有素数
int euler[N]; // 存储每个数的欧拉函数
bool st[N]; // st[x]存储x是否被筛掉
void get_eulers(int n)
{
euler[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!st[i])
{
primes[cnt ++ ] = i;
euler[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j ++ )
{
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0)
{
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
求某一个数的欧拉函数
ll Eoula(int n) {//求φ(m/tmp)
ll res = n;
for (ll i = 2; i*i <= n; i++) {
if (n % i == 0) {
res = res / i * (i - 1);//先除防止数据溢出
while (n % i == 0)n /= i;
}
}
if (n > 1)res = res / n * (n - 1);
return res;
}
快速幂
求 m^k mod p,时间复杂度 O(logk)。
int qpow(int a,int b,int mod){
int ans=1;
while(b){
if(b&1){
ans=(ans*a)%mod;
}
a=(a*a)%mod;
b/=2;
}
return ans;
}
位运算处理大数相乘(1e18)
//0 < a,b,p < 1e18 ;
//求a * b % p
//原理把乘法变成加法
ll quick_add(ll a,ll b,ll p)
{
ll res=0;
while(b)
{
if(b&1) res=(res+a)%p;
a=(a+a)%p;
b>>=1;
}
return res;
}
扩展欧几里得算法
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1; y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= (a/b) * x;
return d;
}
应用的时候可以同时求最大公倍数和二元一次方程的解;
比如:ax+by=k;
如果这个方程组有解,那么k%gcd(a,b)==0;假设有解的情况下去解这个方程;
那么先用exgcd解方程 ax+by=gcd(a,b); 设解为x0,y0;
通解形式:
x=x0+b/gcd(a,b) * n (相当于 x 每次可以增减:b/gcd 的整数倍)
y=y0+a/gcd(a,b) * n (相当于 y 每次可以增减:a/gcd 的整数倍)
《注意:x 求出来后,y 通常由 x 代入方程求得》
最小整数解;
x=(x+b/gcd*n)%(b/gcd) = x%(b/gcd) (b/gcd(a,b) 应取正)
若 x<=0,则 x+=b/gcd
求组合数
打表法求组合数
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
封装预处理C(x,z) 0<=z<=y
void init(int x,int y)
{
C[0][0]=C[1][0] = C[1][1] = 1;
for (int i = 2; i <=x; i++)
{
C[i][0] = 1;
for (int j = 1; j <=y; j++)
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1])%mod;
}
}
逆元的方式求组合数(数据规模上万)
\(A_n^m=\frac{n!}{(n-m)!}\)
\(C_n^m=\frac{n!}{(n-m)!m!}\)
int j[maxn];
typedef long long ll;
ll qpow(ll a,ll b){
ll ans=1;
while(b){
if(b&1){
ans=(ans*a)%mod;
}
a=(a*a)%mod;
b/=2;
}
return ans;
}
void inint(){
j[1]=1;
for(ll i=2;i<maxn;i++){
j[i]=i*j[i-1]%mod;//阶乘打表
}
}
ll C(ll n,ll m){
ll ans=qpow(j[m],mod-2)%mod*qpow(j[n-m],mod-2)%mod;//这是求这两个的逆元
return j[n]*ans%mod;
}
或者先处理处理这些逆元
首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
如果取模的数是质数,可以用费马小定理求逆元
int qmi(int a, int k, int p) // 快速幂模板
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
之后按照公式算就行例如:\(C_n^m=((fact[n]*infact[m])%mod*infact[n-m])%mod\)
Lucas定理(数据规模上亿)
若p是质数,则对于任意整数 1 <= m <= n,有:
C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)
int qmi(int a, int k) // 快速幂模板
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b) // 通过定理求组合数C(a, b)
{
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2) % p;
}
return res;
}
int lucas(LL a, LL b)
{
if (a < p && b < p) return C(a, b);
return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号