优化算法-6.动量法

冲量法也是在实际应用中使用比较多的算法
冲量法使用平滑过的梯度对权重更新

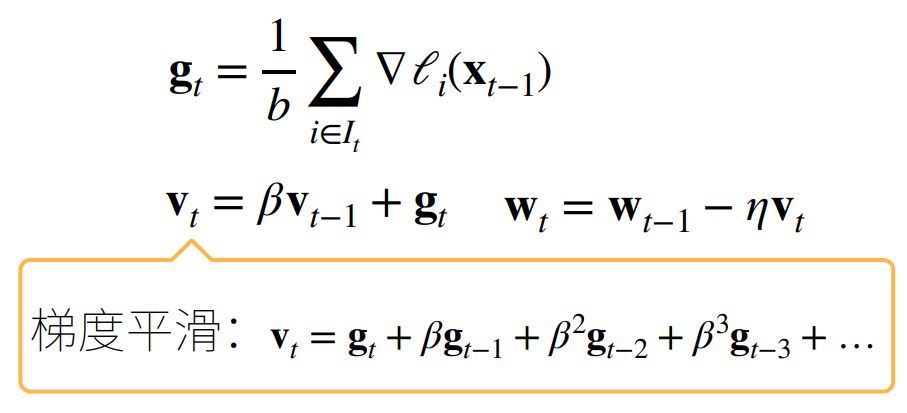
在小批量随机梯度下降的时候，梯度还是会有比较大的抖动，特别是当整个目标函数比较复杂的时候
真实数据的损失函数是不平滑的，在一个不那么平滑的平面上做优化的时候，梯度的变化趋势就有点类似于随机运动，噪音可能会带来一些不必要的抖动
冲量法中，它维护了一个惯性，使得梯度变化的方向不要变化太快，方向还是要改变的，这是变化起来比较平滑
\(v_t\)实际上是等于当前时刻的梯度+ \(\beta \times\)上一个时刻的梯度 + \(\beta \times \beta \times\)上上个时刻的梯度...
\(\beta\) 是一个小于 1 的值，所以\(v_t\)中历史时刻的梯度项随着时间的下降存在指数级的减少，时间越早的梯度项，最后的值就越小
通过这样的设计使得对整个权重更新的方向并不是完全取决于\(g_t\)，还要参考过去时间的梯度，如果当前时刻的\(g_t\)和上一时刻的\(g_{t-1}\)完全不同的话，使得\(g_{t-1}\)能够通过\(\beta\)对\(g_t\)变化的方向进行一定程度的抵消，使得更新不那么剧烈
\(\beta\)常见的取值：0.5、0.9、0.95、0.99。假设\(\beta\)取 0.5 的话，\(v_t\)中历史时刻的梯度项会衰减得特别快（大概是计算过去两三个时刻的梯度取平均）。假设\(\beta\)取 0.99 的话，\(v_t\)中历史时刻的梯度项会衰减得比较慢，可以认为\(g_t\)的变化会参考过去几十个时刻梯度的方向（大概是计算过去五十个时刻的梯度取平均，超过 50 个以外的那些梯度项就变得很小了，几乎可以忽略不计）
如果说样本数量比较大，β 取 0.99 也很正常
对比随机梯度下降(下)和冲量法(上)

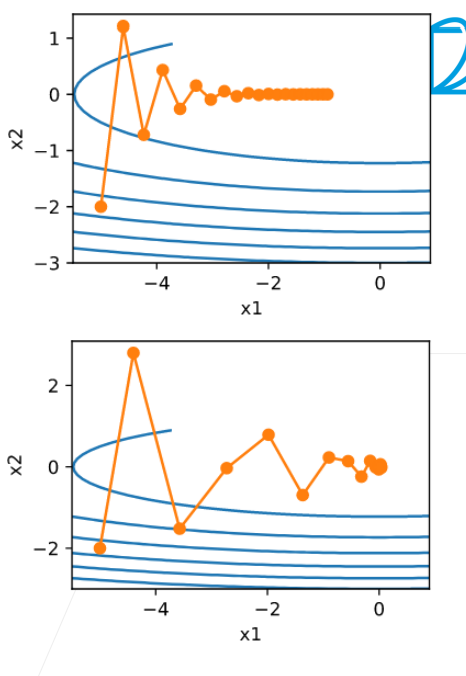
随机梯度下降上下振动的幅度比较大
冲量法是几个相互冲突的方向在慢慢相互抵消，使得梯度的变化尽量朝着正确的方向
通过框架中的 moment 这个超参数来设定冲量法，最简单的 sgd 都有 moment 的选项，只需要将 moment 设置成自己想要的值就可以了

我们详述了如何执行随机梯度下降，即在只有嘈杂的梯度可用的情况下执行优化时会发生什么。对于嘈杂的梯度，我们在选择学习率需要格外谨慎。如果衰减速度太快，收敛就会停滞。相反，如果太宽松，我们可能无法收敛到最优解。

基础

本节将探讨更有效的优化算法，尤其是针对实验中常见的某些类型的优化问题。

泄漏平均值

上一节中我们讨论了小批量随机梯度下降作为加速计算的手段。它也有很好的副作用，即平均梯度减小了方差。小批量随机梯度下降可以通过以下方式计算：

\[\mathbf{g}_{t, t-1} = \partial_{\mathbf{w}} \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} f(\mathbf{x}_{i}, \mathbf{w}_{t-1}) = \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} \mathbf{h}_{i, t-1}. \]

为了保持记法简单，在这里我们使用\(\mathbf{h}_{i, t-1} = \partial_{\mathbf{w}} f(\mathbf{x}_i, \mathbf{w}_{t-1})\)作为样本的随机梯度下降，使用时间\(t-1\)时更新的权重\(t-1\)。如果我们能够从方差减少的影响中受益，甚至超过小批量上的梯度平均值，那很不错。完成这项任务的一种选择是用泄漏平均值（leaky average）取代梯度计算：

\[\mathbf{v}_t = \beta \mathbf{v}_{t-1} + \mathbf{g}_{t, t-1} \]

其中\(\beta \in (0, 1)\)。这有效地将瞬时梯度替换为多个“过去”梯度的平均值。\(\mathbf{v}\)被称为动量（momentum），它累加了过去的梯度。为了更详细地解释，让我们递归地将\(\mathbf{v}_t\)扩展到

\[\begin{aligned} \mathbf{v}_t = \beta^2 \mathbf{v}_{t-2} + \beta \mathbf{g}_{t-1, t-2} + \mathbf{g}_{t, t-1} = \ldots, = \sum_{\tau = 0}^{t-1} \beta^{\tau} \mathbf{g}_{t-\tau, t-\tau-1}. \end{aligned}\]

其中，较大的\(\beta\)相当于长期平均值，而较小的\(\beta\)相对于梯度法只是略有修正。新的梯度替换不再指向特定实例下降最陡的方向，而是指向过去梯度的加权平均值的方向。这使我们能够实现对单批量计算平均值的大部分好处，而不产生实际计算其梯度的代价。

上述推理构成了“加速”梯度方法的基础，例如具有动量的梯度。在优化问题条件不佳的情况下（例如，有些方向的进展比其他方向慢得多，类似狭窄的峡谷），“加速”梯度还额外享受更有效的好处。此外，它们允许我们对随后的梯度计算平均值，以获得更稳定的下降方向。诚然，即使是对于无噪声凸问题，加速度这方面也是动量如此起效的关键原因之一。

正如人们所期望的，由于其功效，动量是深度学习及其后优化中一个深入研究的主题。

条件不佳的问题

为了更好地了解动量法的几何属性，我们复习一下梯度下降，尽管它的目标函数明显不那么令人愉快。对于这个函数\(f(\mathbf{x}) = x_1^2 + 2 x_2^2\)
，即中度扭曲的椭球目标。我们通过向\(x_1\)方向伸展它来进一步扭曲这个函数

\[f(\mathbf{x}) = 0.1 x_1^2 + 2 x_2^2. \]

与之前一样，\(f\)在\((0,0)\)有最小值，该函数在\(x_1\)的方向上非常平坦。让我们看看在这个新函数上执行梯度下降时会发生什么。

%matplotlib inline
import torch
from d2l import torch as d2l

eta = 0.4
def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

epoch 20, x1: -0.943467, x2: -0.000073

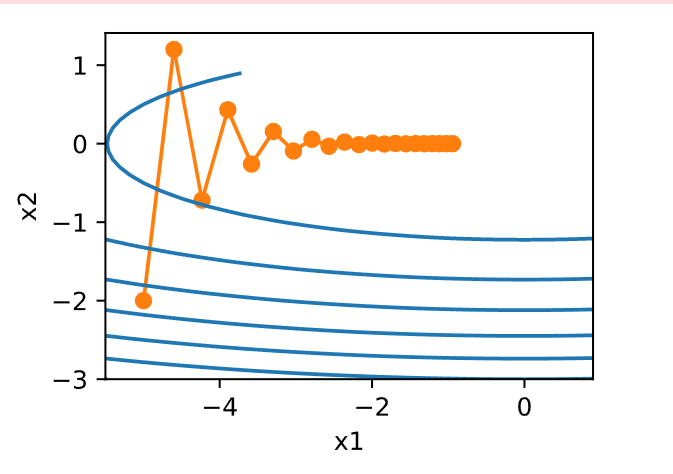
从构造来看，\(x_2\)方向的梯度比水平\(x_1\)方向的梯度大得多，变化也快得多。因此，我们陷入两难：如果选择较小的学习率，我们会确保解不会在方向\(x_2\)发散，但要承受在\(x_1\)方向的缓慢收敛。相反，如果学习率较高，我们在\(x_1\)方向上进展很快，但在\(x_2\)方向将会发散。下面的例子说明了即使学习率从\(0.4\)略微提高到\(0.6\)，也会发生变化。 \(x_1\)方向上的收敛有所改善，但整体来看解的质量更差了。

eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

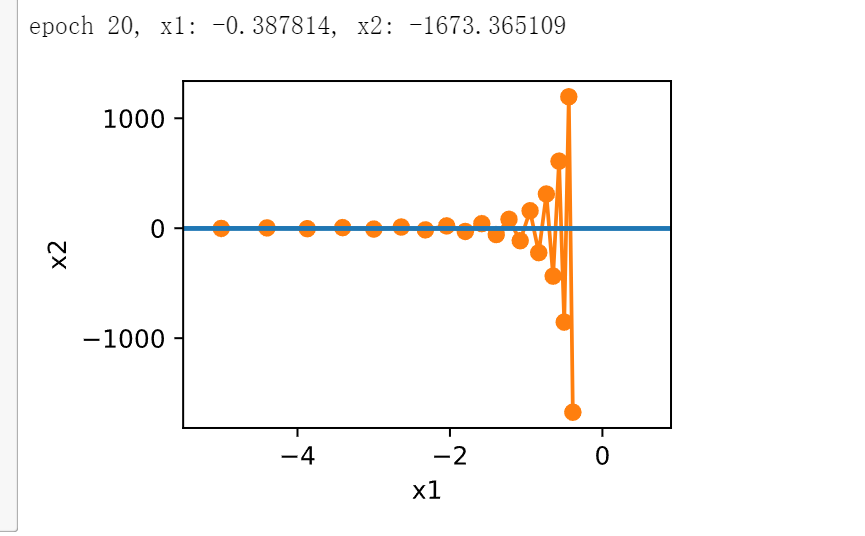
动量法

动量法（momentum）使我们能够解决上面描述的梯度下降问题。观察上面的优化轨迹，我们可能会直觉到计算过去的平均梯度效果会很好。毕竟，在\(x_1\)方向上，这将聚合非常对齐的梯度，从而增加我们在每一步中覆盖的距离。相反，在梯度振荡的\(x_2\)方向，由于相互抵消了对方的振荡，聚合梯度将减小步长大小。使用\(\mathbf{v}_t\)而不是梯度\(\mathbf{g}_t\)可以生成以下更新等式：

\[\begin{split}\begin{aligned} \mathbf{v}_t &\leftarrow \beta \mathbf{v}_{t-1} + \mathbf{g}_{t, t-1}, \\ \mathbf{x}_t &\leftarrow \mathbf{x}_{t-1} - \eta_t \mathbf{v}_t. \end{aligned}\end{split}\]

请注意，对于\(\beta = 0\)，我们恢复常规的梯度下降。在深入研究它的数学属性之前，让我们快速看一下算法在实验中的表现如何。

def momentum_2d(x1, x2, v1, v2):
    v1 = beta * v1 + 0.2 * x1
    v2 = beta * v2 + 4 * x2
    return x1 - eta * v1, x2 - eta * v2, v1, v2

eta, beta = 0.6, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

epoch 20, x1: 0.007188, x2: 0.002553

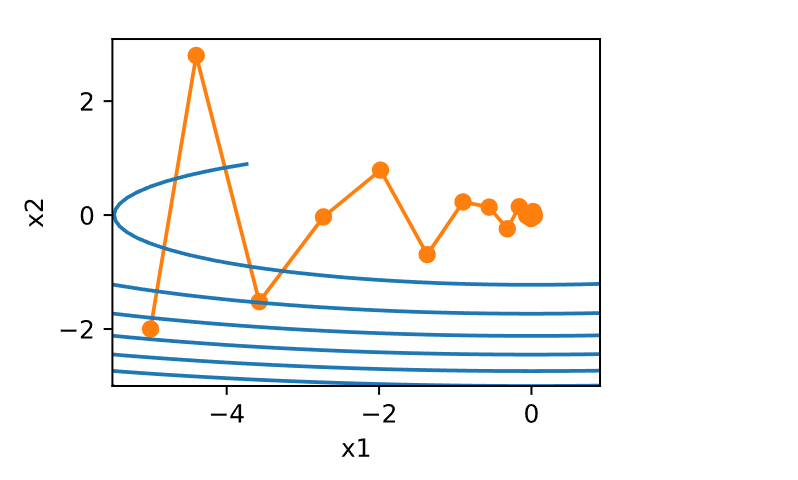
正如所见，尽管学习率与我们以前使用的相同，动量法仍然很好地收敛了。让我们看看当降低动量参数时会发生什么。将其减半至\(\beta = 0.25\)会导致一条几乎没有收敛的轨迹。尽管如此，它比没有动量时解将会发散要好得多。

eta, beta = 0.6, 0.25
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

epoch 20, x1: -0.126340, x2: -0.186632

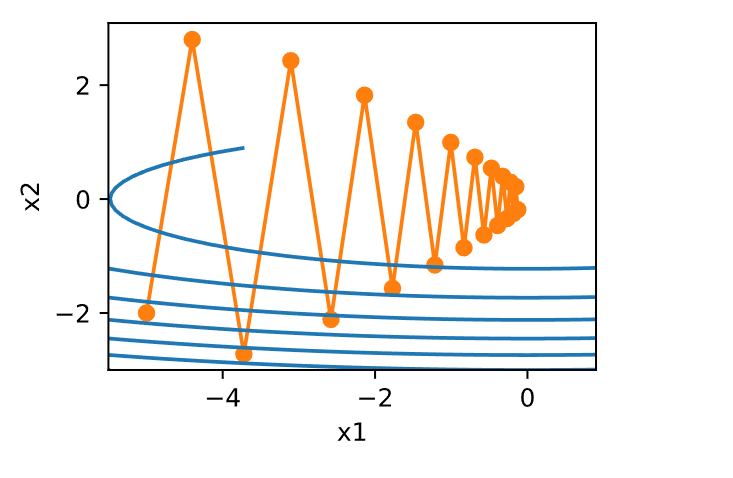
请注意，我们可以将动量法与随机梯度下降，特别是小批量随机梯度下降结合起来。唯一的变化是，在这种情况下，我们将梯度\(\mathbf{g}_{t, t-1}\)替换为\(g_t\)。为了方便起见，我们在时间\(t=0\)初始化\(v_0=0\)。

有效样本权重

回想一下\(\mathbf{v}_t = \sum_{\tau = 0}^{t-1} \beta^{\tau} \mathbf{g}_{t-\tau, t-\tau-1}\)。极限条件下，\(\sum_{\tau=0}^\infty \beta^\tau = \frac{1}{1-\beta}\)。换句话说，不同于在梯度下降或者随机梯度下降中取步长\(\eta\)，我们选取步长
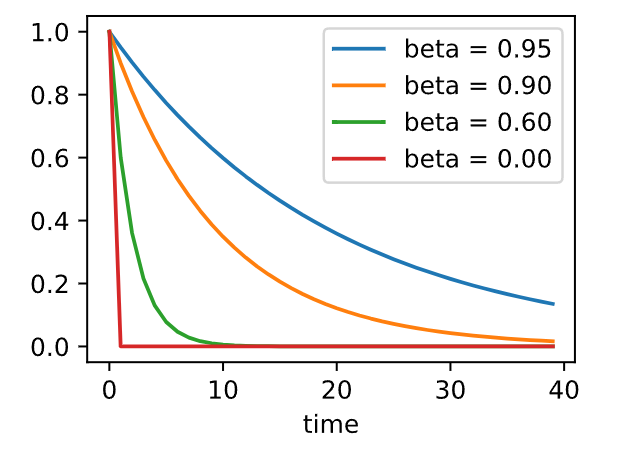
\(\frac{\eta}{1-\beta}\)，同时处理潜在表现可能会更好的下降方向。这是集两种好处于一身的做法。为了说明\(\beta\)的不同选择的权重效果如何，请参考下面的图表。

d2l.set_figsize()
betas = [0.95, 0.9, 0.6, 0]
for beta in betas:
    x = torch.arange(40).detach().numpy()
    d2l.plt.plot(x, beta ** x, label=f'beta = {beta:.2f}')
d2l.plt.xlabel('time')
d2l.plt.legend();

实际实验

让我们来看看动量法在实验中是如何运作的。为此，我们需要一个更加可扩展的实现。

从零开始实现

相比于小批量随机梯度下降，动量方法需要维护一组辅助变量，即速度。它与梯度以及优化问题的变量具有相同的形状。在下面的实现中，我们称这些变量为states。

def init_momentum_states(feature_dim):
    v_w = torch.zeros((feature_dim, 1))
    v_b = torch.zeros(1)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        with torch.no_grad():
            v[:] = hyperparams['momentum'] * v + p.grad
            p[:] -= hyperparams['lr'] * v
        p.grad.data.zero_()

让我们看看它在实验中是如何运作的。

def train_momentum(lr, momentum, num_epochs=2):
    d2l.train_ch11(sgd_momentum, init_momentum_states(feature_dim),
                   {'lr': lr, 'momentum': momentum}, data_iter,
                   feature_dim, num_epochs)

data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
train_momentum(0.02, 0.5)

loss: 0.246, 0.013 sec/epoch

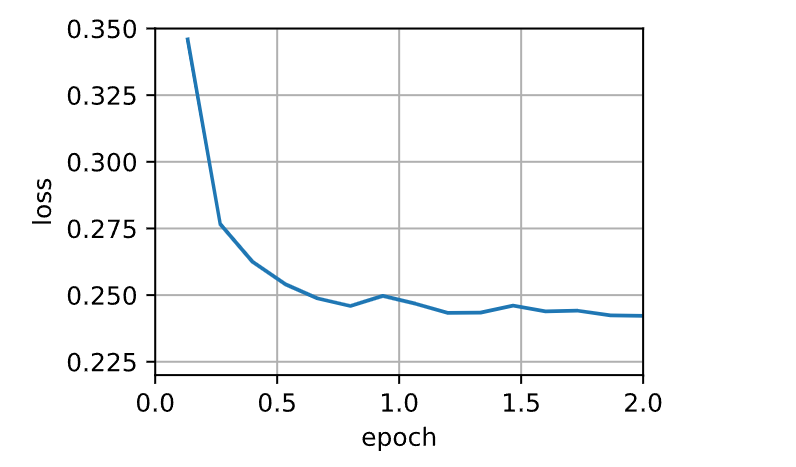
当我们将动量超参数momentum增加到0.9时，它相当于有效样本数量增加到
\(\frac{1}{1 - 0.9} = 10\)。我们将学习率略微降至\(0.01\)，以确保可控。

train_momentum(0.01, 0.9)

loss: 0.261, 0.013 sec/epoch

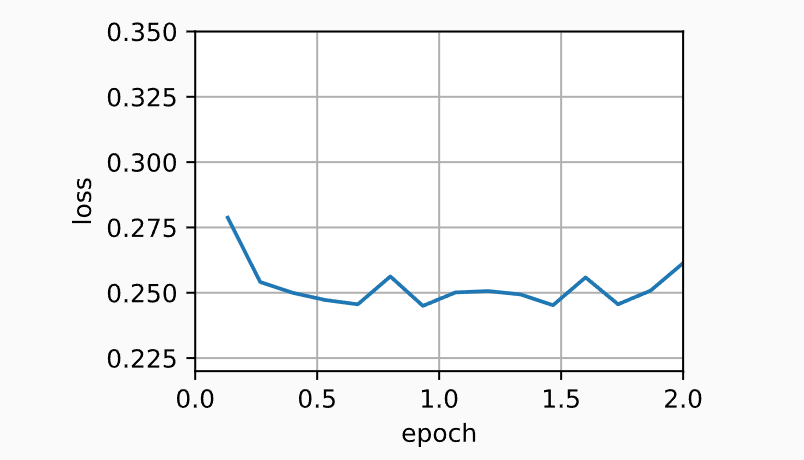
降低学习率进一步解决了任何非平滑优化问题的困难，将其设置为\(0.005\)会产生良好的收敛性能。

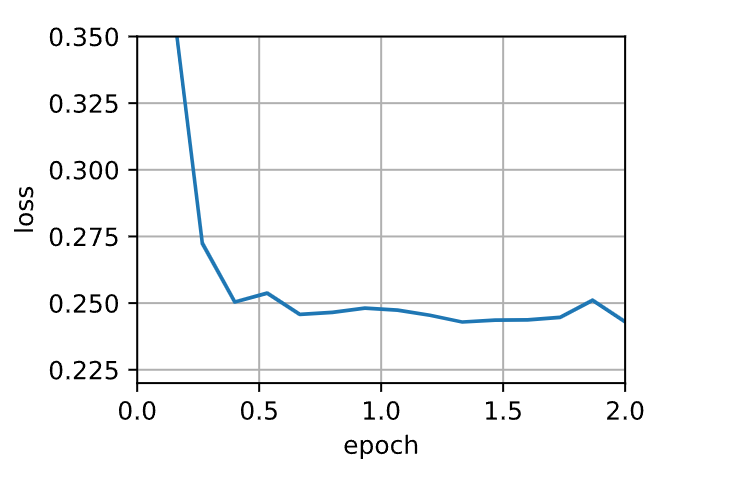
train_momentum(0.005, 0.9)

loss: 0.243, 0.008 sec/epoch

简洁实现

trainer = torch.optim.SGD
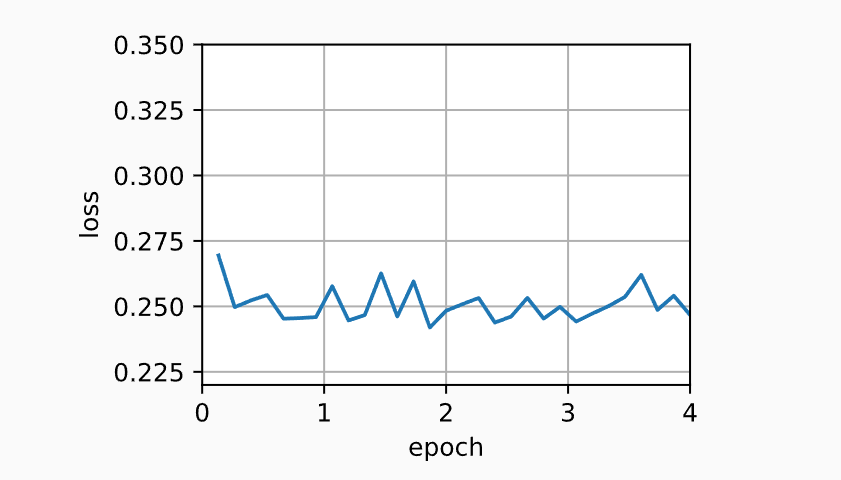
d2l.train_concise_ch11(trainer, {'lr': 0.005, 'momentum': 0.9}, data_iter)

loss: 0.247, 0.012 sec/epoch

posted @ 2023-10-05 15:12 lipu123 阅读(314) 评论(0) 收藏举报

刷新页面返回顶部

lipu123