优化算法-3.梯度下降

梯度下降法

尽管梯度下降（gradient descent）很少直接用于深度学习， 但了解它是理解下一节随机梯度下降算法的关键。 例如，由于学习率过大，优化问题可能会发散，这种现象早已在梯度下降中出现。 同样地，预处理（preconditioning）是梯度下降中的一种常用技术， 还被沿用到更高级的算法中。 让我们从简单的一维梯度下降开始。

一维梯度下降

梯度下降算法是最简单的迭代求解算法：

首先选取开始点\(x_0\),对\(t=1,...,T\)，我们有

\[x_t=x_{t-1}-\eta \nabla f(x_{t-1}) \]

其中\(\eta\)叫做学习率。\(\nabla f(x_{t-1})\)是f(x_{t-1})的梯度，它的梯度是朝着\(f(x)\)值增大的方向，所以这个是负的。

为什么梯度下降算法可以优化目标函数？ 一维中的梯度下降给我们很好的启发。 考虑一类连续可微实值函数\(f: \mathbb{R} \rightarrow \mathbb{R}\)， 利用泰勒展开，我们可以得到

\[f(x + \epsilon) = f(x) + \epsilon f'(x) + \mathcal{O}(\epsilon^2). \]

即在一阶近似中，\(f(x+\epsilon)\)可通过处的函数值\(f(x)\)和一阶导数\(f'(x)\)得出。 我们可以假设在负梯度方向上移动的\(\epsilon\)会减少\(f\)。 为了简单起见，我们选择固定步长\(\eta > 0\)，然后取\(\epsilon = -\eta f'(x)\)。 将其代入泰勒展开式我们可以得到

\[f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + \mathcal{O}(\eta^2 f'^2(x)). \]

如果其导数\(f'(x) \neq 0\)没有消失，我们就能继续展开，这是因为\(\eta f'^2(x)>0\)。 此外，我们总是可以令\(\eta\)小到足以使高阶项变得不相关。 因此，

\[f(x - \eta f'(x)) \lessapprox f(x). \]

这意味着，如果我们使用

\[x \leftarrow x - \eta f'(x) \]

来迭代\(x\)，函数\(f(x)\)的值可能会下降。 因此，在梯度下降中，我们首先选择初始值\(x\)和常数\(\eta > 0\)， 然后使用它们连续迭代\(x\)，直到停止条件达成。 例如，当梯度\(|f'(x)|\)的幅度足够小或迭代次数达到某个值时。
下面我们来展示如何实现梯度下降。为了简单起见，我们选用目标函数\(f(x)=x^2\)。 尽管我们知道\(x=0\)时\(f(x)\)能取得最小值， 但我们仍然使用这个简单的函数来观察\(x\)的变化

%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

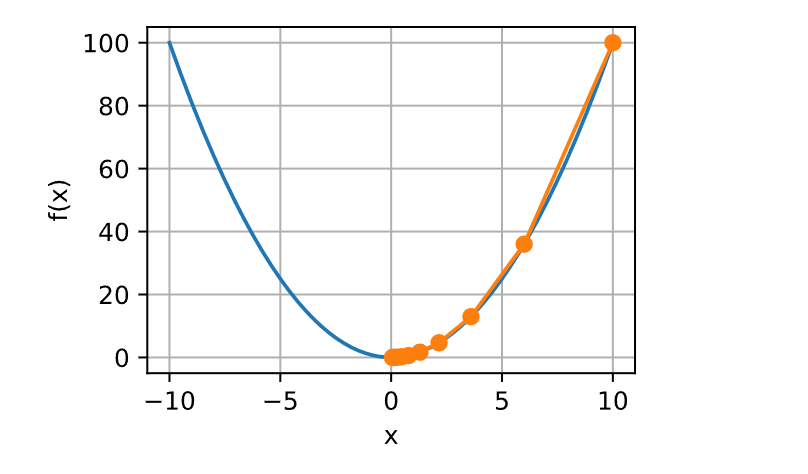
接下来，我们使用\(x=10\)作为初始值，并假设\(\eta=0.2\)。 使用梯度下降法迭代\(x\)共10次，我们可以看到，\(x\)的值最终将接近最优解。

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(float(x))
        print(f'epoch {i:d}, x: {x:f}')
    return results

results = gd(0.2, f_grad)

对\(x\)进行优化的过程可以绘制如下。

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = torch.arange(-n, n, 0.01)
    d2l.set_figsize()
    d2l.plot([f_line, results], [[f(x) for x in f_line], [
        f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])

show_trace(results, f)

学习率

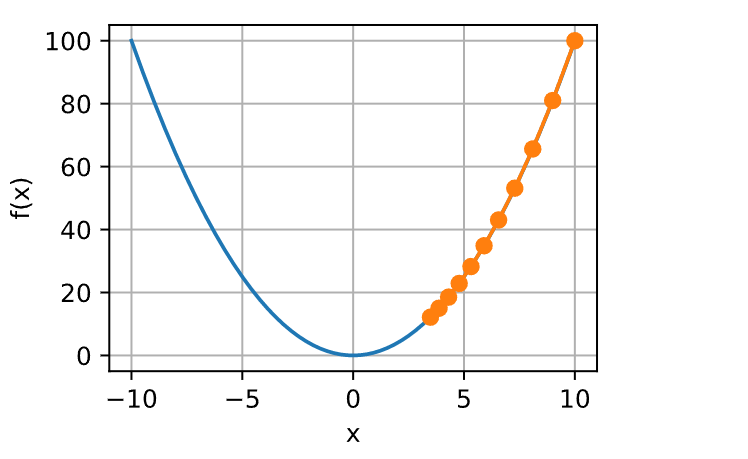
学习率（learning rate）决定目标函数能否收敛到局部最小值，以及何时收敛到最小值。 学习率\(\eta\)可由算法设计者设置。 请注意，如果我们使用的学习率太小，将导致\(x\)的更新非常缓慢，需要更多的迭代。 例如，考虑同一优化问题中\(\eta = 0.05\)的进度。 如下所示，尽管经过了10个步骤，我们仍然离最优解很远。

show_trace(gd(0.05, f_grad), f)

epoch 0, x: 9.000000
epoch 1, x: 8.100000
epoch 2, x: 7.290000
epoch 3, x: 6.561000
epoch 4, x: 5.904900
epoch 5, x: 5.314410
epoch 6, x: 4.782969
epoch 7, x: 4.304672
epoch 8, x: 3.874205
epoch 9, x: 3.486784

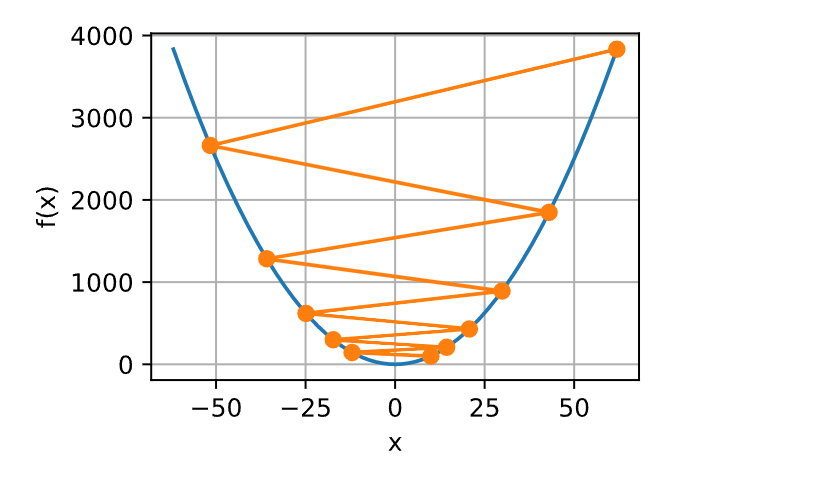
相反，如果我们使用过高的学习率，\(\left|\eta f'(x)\right|\)对于一阶泰勒展开式可能太大。 也就是说，\(\mathcal{O}(\eta^2 f'^2(x))\)可能变得显著了。 在这种情况下，\(x\)的迭代不能保证降低\(f(x)\)的值。 例如，当学习率为\(\eta=1.1\)时，\(x\)超出了最优解\(x=0\)并逐渐发散。

show_trace(gd(1.1, f_grad), f)

epoch 0, x: -12.000000
epoch 1, x: 14.400000
epoch 2, x: -17.280000
epoch 3, x: 20.736000
epoch 4, x: -24.883200
epoch 5, x: 29.859840
epoch 6, x: -35.831808
epoch 7, x: 42.998170
epoch 8, x: -51.597804
epoch 9, x: 61.917364

局部最小值

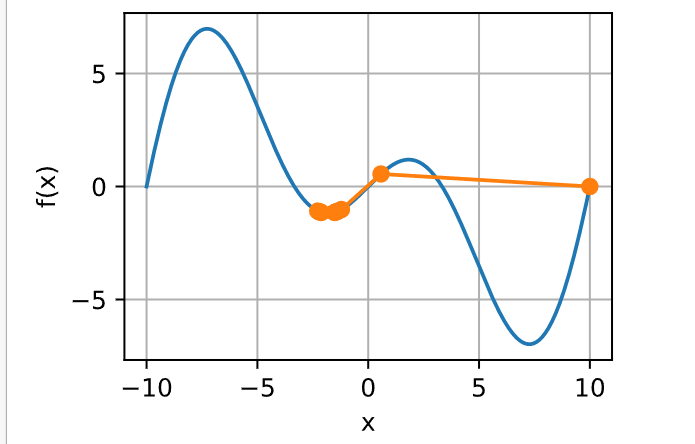
为了演示非凸函数的梯度下降，考虑函数\(f(x) = x \cdot \cos(cx)\)，其中\(c\)为某常数。 这个函数有无穷多个局部最小值。 根据我们选择的学习率，我们最终可能只会得到许多解的一个。 下面的例子说明了（不切实际的）高学习率如何导致较差的局部最小值。

c = torch.tensor(0.15 * np.pi)

def f(x):  # 目标函数
    return x * torch.cos(c * x)

def f_grad(x):  # 目标函数的梯度
    return torch.cos(c * x) - c * x * torch.sin(c * x)

show_trace(gd(2, f_grad), f)

epoch 0, x: 0.575222
epoch 1, x: -1.206588
epoch 2, x: -2.279598
epoch 3, x: -1.343416
epoch 4, x: -2.206769
epoch 5, x: -1.425789
epoch 6, x: -2.154634
epoch 7, x: -1.483876
epoch 8, x: -2.114354
epoch 9, x: -1.528166

多元梯度下降

现在我们对单变量的情况有了更好的理解，让我们考虑一下\(\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top\)的情况。 即目标函数\(f: \mathbb{R}^d \to \mathbb{R}\)将向量映射成标量。 相应地，它的梯度也是多元的，它是一个由\(d\)个偏导数组成的向量：

\[\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top. \]

梯度中的每个偏导数元素\(\partial f(\mathbf{x})/\partial x_i\)代表了当输入\(x_i\)时\(f\)在\(x\)处的变化率。 和先前单变量的情况一样，我们可以对多变量函数使用相应的泰勒近似来思考。 具体来说，

\[f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \mathbf{\boldsymbol{\epsilon}}^\top \nabla f(\mathbf{x}) + \mathcal{O}(\|\boldsymbol{\epsilon}\|^2). \]

换句话说，在\(\boldsymbol{\epsilon}\)的二阶项中， 最陡下降的方向由负梯度\(-\nabla f(\mathbf{x})\)得出。 选择合适的学习率\(\eta > 0\)来生成典型的梯度下降算法：

\[\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x}). \]

这个算法在实践中的表现如何呢？ 我们构造一个目标函数\(f(\mathbf{x})=x_1^2+2x_2^2\)， 并有二维向量\(\mathbf{x} = [x_1, x_2]^\top\)作为输入， 标量作为输出。 梯度由\(\nabla f(\mathbf{x}) = [2x_1, 4x_2]^\top\)给出。 我们将从初始位置\([-5, -2]\)通过梯度下降观察\(x\)的轨迹。
我们还需要两个辅助函数： 第一个是update函数，并将其应用于初始值20次； 第二个函数会显示\(x\)的轨迹。

def train_2d(trainer, steps=20, f_grad=None):  #@save
    """用定制的训练机优化2D目标函数"""
    # s1和s2是稍后将使用的内部状态变量
    x1, x2, s1, s2 = -5, -2, 0, 0
    results = [(x1, x2)]
    for i in range(steps):
        if f_grad:
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
        else:
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
    print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
    return results

def show_trace_2d(f, results):  #@save
    """显示优化过程中2D变量的轨迹"""
    d2l.set_figsize()
    d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = torch.meshgrid(torch.arange(-5.5, 1.0, 0.1),
                          torch.arange(-3.0, 1.0, 0.1), indexing='ij')
    d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')

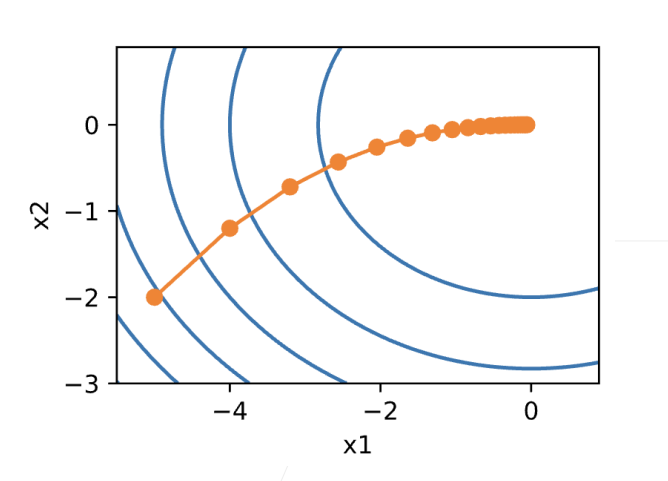
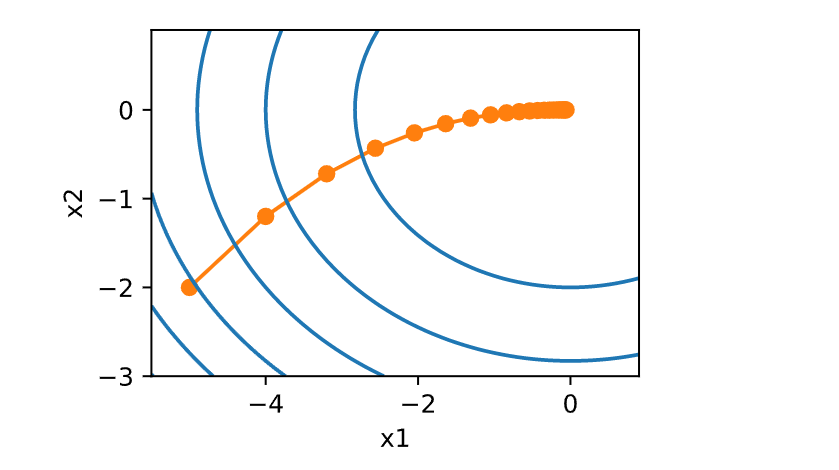
接下来，我们观察学习率\(\eta = 0.1\)时优化变量\(x\)的轨迹。 可以看到，经过20步之后，\(x\)的值接近其位于\([0, 0]\)的最小值。 虽然进展相当顺利，但相当缓慢。

def f_2d(x1, x2):  # 目标函数
    return x1 ** 2 + 2 * x2 ** 2

def f_2d_grad(x1, x2):  # 目标函数的梯度
    return (2 * x1, 4 * x2)

def gd_2d(x1, x2, s1, s2, f_grad):
    g1, g2 = f_grad(x1, x2)
    return (x1 - eta * g1, x2 - eta * g2, 0, 0)

eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))

epoch 1, x1: -4.000000, x2: -1.200000
epoch 2, x1: -3.200000, x2: -0.720000
epoch 3, x1: -2.560000, x2: -0.432000
epoch 4, x1: -2.048000, x2: -0.259200
epoch 5, x1: -1.638400, x2: -0.155520
epoch 6, x1: -1.310720, x2: -0.093312
epoch 7, x1: -1.048576, x2: -0.055987
epoch 8, x1: -0.838861, x2: -0.033592
epoch 9, x1: -0.671089, x2: -0.020155
epoch 10, x1: -0.536871, x2: -0.012093
epoch 11, x1: -0.429497, x2: -0.007256
epoch 12, x1: -0.343597, x2: -0.004354
epoch 13, x1: -0.274878, x2: -0.002612
epoch 14, x1: -0.219902, x2: -0.001567
epoch 15, x1: -0.175922, x2: -0.000940
epoch 16, x1: -0.140737, x2: -0.000564
epoch 17, x1: -0.112590, x2: -0.000339
epoch 18, x1: -0.090072, x2: -0.000203
epoch 19, x1: -0.072058, x2: -0.000122
epoch 20, x1: -0.057646, x2: -0.000073

自适应方法

选择"恰到好处"的学习率\(\eta\)是很棘手的。如果我们把它选得太小，就没有什么进展；如果太大，得到的解就会振荡，甚至可能发散。 如果我们可以自动确定\(\eta\)，或者完全不必选择学习率，会怎么样？ 除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法可以帮我们解决这个问题。 虽然由于计算代价的原因，这些方法不能直接应用于深度学习，但它们为如何设计高级优化算法提供了有用的思维直觉，这些算法可以模拟下面概述的算法的许多理想特性。

牛顿法

回顾一些函数\(f: \mathbb{R}^d \rightarrow \mathbb{R}\)的泰勒展开式，事实上我们可以把它写成

\[f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \boldsymbol{\epsilon}^\top \nabla f(\mathbf{x}) + \frac{1}{2} \boldsymbol{\epsilon}^\top \nabla^2 f(\mathbf{x}) \boldsymbol{\epsilon} + \mathcal{O}(\|\boldsymbol{\epsilon}\|^3). \]

为了避免繁琐的符号，我们将\(\mathbf{H} \stackrel{\mathrm{def}}{=} \nabla^2 f(\mathbf{x})\)定义为的Hessian，是\(d \times d\)矩阵。 当\(d\)的值很小且问题很简单时，\(\mathbf{H}\)很容易计算。 但是对于深度神经网络而言，考虑到\(\mathbf{H}\)可能非常大， \(\mathcal{O}(d^2)\)个条目的存储代价会很高， 此外通过反向传播进行计算可能雪上加霜。 然而，我们姑且先忽略这些考量，看看会得到什么算法。
毕竟，\(f\)的最小值满足\(\nabla f = 0\)。 遵循微积分规则， 通过取\(\boldsymbol{\epsilon}\)对上式的导数， 再忽略不重要的高阶项，我们便得到

\[\nabla f(\mathbf{x}) + \mathbf{H} \boldsymbol{\epsilon} = 0 \text{ and hence } \boldsymbol{\epsilon} = -\mathbf{H}^{-1} \nabla f(\mathbf{x}).\]

也就是说，作为优化问题的一部分，我们需要将Hessian矩阵\(\mathbf{H}\)求逆。
举一个简单的例子，对于\(f(x) = \frac{1}{2} x^2\)，我们有\(\nabla f(x) = x\)和\(\mathbf{H} = 1\)。 因此，对于任何\(x\)，我们可以获得\(\epsilon = -x\)。 换言之，单单一步就足以完美地收敛，而无须任何调整。 我们在这里比较幸运：泰勒展开式是确切的，因为\(f(x+\epsilon)= \frac{1}{2} x^2 + \epsilon x + \frac{1}{2} \epsilon^2\)。
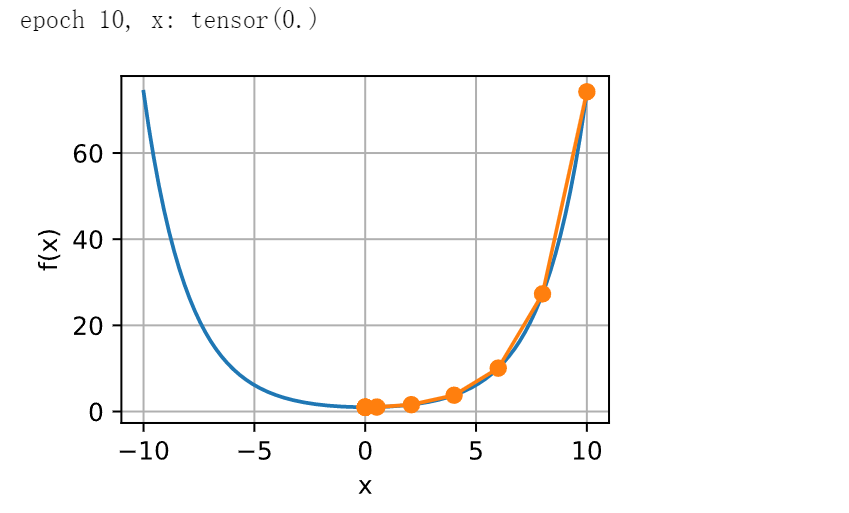
让我们看看其他问题。 给定一个凸双曲余弦函数\(c\)，其中\(c\)为某些常数， 我们可以看到经过几次迭代后，得到了\(x=0\)处的全局最小值。

c = torch.tensor(0.5)

def f(x):  # O目标函数
    return torch.cosh(c * x)

def f_grad(x):  # 目标函数的梯度
    return c * torch.sinh(c * x)

def f_hess(x):  # 目标函数的Hessian
    return c**2 * torch.cosh(c * x)

def newton(eta=1):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x) / f_hess(x)
        results.append(float(x))
    print('epoch 10, x:', x)
    return results

show_trace(newton(), f)

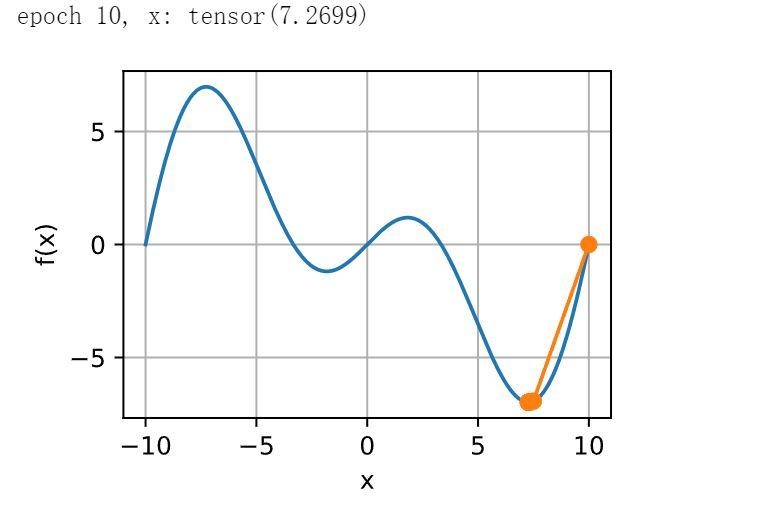
现在让我们考虑一个非凸函数，比如\(f(x) = x \cos(c x)\)，\(c\)为某些常数。 请注意在牛顿法中，我们最终将除以Hessian。 这意味着如果二阶导数是负的，的值可能会趋于增加。 这是这个算法的致命缺陷！ 让我们看看实践中会发生什么。

c = torch.tensor(0.15 * np.pi)

def f(x):  # 目标函数
    return x * torch.cos(c * x)

def f_grad(x):  # 目标函数的梯度
    return torch.cos(c * x) - c * x * torch.sin(c * x)

def f_hess(x):  # 目标函数的Hessian
    return - 2 * c * torch.sin(c * x) - x * c**2 * torch.cos(c * x)

show_trace(newton(), f)

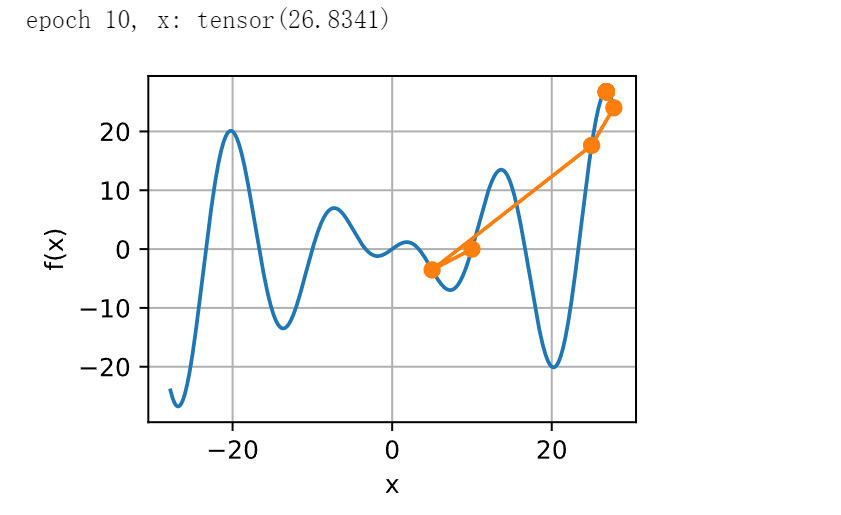
这发生了惊人的错误。我们怎样才能修正它？ 一种方法是用取Hessian的绝对值来修正，另一个策略是重新引入学习率。 这似乎违背了初衷，但不完全是——拥有二阶信息可以使我们在曲率较大时保持谨慎，而在目标函数较平坦时则采用较大的学习率。 让我们看看在学习率稍小的情况下它是如何生效的，比如\(\eta = 0.5\)。 如我们所见，我们有了一个相当高效的算法。

show_trace(newton(0.5), f)

收敛性分析

在此，我们以部分目标凸函数\(f\)为例，分析它们的牛顿法收敛速度。 这些目标凸函数三次可微，而且二阶导数不为零，即\(f'' > 0\)。 由于多变量情况下的证明是对以下一维参数情况证明的直接拓展，对我们理解这个问题不能提供更多帮助，因此我们省略了多变量情况的证明。
用\(x^{(k)}\)表示\(x\)在第\(k^\mathrm{th}\)次迭代时的值， 令$e^{(k)} \stackrel{\mathrm{def}}{=} x^{(k)} - x^* \(表示\)k^\mathrm{th}\(迭代时与最优性的距离。 通过泰勒展开，我们得到条件\)f'(x^*) = 0$可以写成

\[0 = f'(x^{(k)} - e^{(k)}) = f'(x^{(k)}) - e^{(k)} f''(x^{(k)}) + \frac{1}{2} (e^{(k)})^2 f'''(\xi^{(k)}), \]

这对某些\(\xi^{(k)} \in [x^{(k)} - e^{(k)}, x^{(k)}]\)成立。 将上述展开除以\(f''(x^{(k)})\)得到

\[e^{(k)} - \frac{f'(x^{(k)})}{f''(x^{(k)})} = \frac{1}{2} (e^{(k)})^2 \frac{f'''(\xi^{(k)})}{f''(x^{(k)})}. \]

回想之前的方程\(x^{(k+1)} = x^{(k)} - f'(x^{(k)}) / f''(x^{(k)})\)。 代入这个更新方程，取两边的绝对值，我们得到

\[\left|e^{(k+1)}\right| = \frac{1}{2}(e^{(k)})^2 \frac{\left|f'''(\xi^{(k)})\right|}{f''(x^{(k)})}. \]

因此，每当我们处于有界区域\(\left|f'''(\xi^{(k)})\right| / (2f''(x^{(k)})) \leq c\)， 我们就有一个二次递减误差

\[\left|e^{(k+1)}\right| \leq c (e^{(k)})^2. \]

另一方面，优化研究人员称之为“线性”收敛，而将\(\left|e^{(k+1)}\right| \leq \alpha \left|e^{(k)}\right|\)这样的条件称为“恒定”收敛速度。 请注意，我们无法估计整体收敛的速度，但是一旦我们接近极小值，收敛将变得非常快。 另外，这种分析\(f\)要求在高阶导数上表现良好，即确保\(f\)在如何变化它的值方面没有任何“超常”的特性。

预处理

计算和存储完整的Hessian非常昂贵，而改善这个问题的一种方法是“预处理”。 它回避了计算整个Hessian，而只计算“对角线”项，即如下的算法更新：

\[\mathbf{x} \leftarrow \mathbf{x} - \eta \mathrm{diag}(\mathbf{H})^{-1} \nabla f(\mathbf{x}). \]

虽然这不如完整的牛顿法精确，但它仍然比不使用要好得多。 为什么预处理有效呢？ 假设一个变量以毫米表示高度，另一个变量以公里表示高度的情况。 假设这两种自然尺度都以米为单位，那么我们的参数化就出现了严重的不匹配。 幸运的是，使用预处理可以消除这种情况。 梯度下降的有效预处理相当于为每个变量选择不同的学习率（矢量\(\mathbf{x}\)的坐标）。 我们将在后面一节看到，预处理推动了随机梯度下降优化算法的一些创新。

梯度下降和线搜索

梯度下降的一个关键问题是我们可能会超过目标或进展不足， 解决这一问题的简单方法是结合使用线搜索和梯度下降。 也就是说，我们使用\(\nabla f(\mathbf{x})\)给出的方向， 然后进行二分搜索，以确定哪个学习率\(\eta\)使\(f(\mathbf{x} - \eta \nabla f(\mathbf{x}))\)取最小值。

小结

• 学习率的大小很重要：学习率太大会使模型发散，学习率太小会没有进展。

• 梯度下降会可能陷入局部极小值，而得不到全局最小值。

• 在高维模型中，调整学习率是很复杂的。

• 预处理有助于调节比例。

• 牛顿法在凸问题中一旦开始正常工作，速度就会快得多。

• 对于非凸问题，不要不作任何调整就使用牛顿法。