注意力机制

生物学中的注意力提示

受试者基于非自主性提示和自主性提示有选择地引导注意力的焦点。
非自主性提示是基于环境中物体的突出性和易见性。想象一下，假如我们面前有五个物品：一份报纸、一篇研究论文、一杯咖啡、一本笔记本和一本书。所有纸制品都是黑白印刷的，但咖啡杯是红色的。换句话说，这个咖啡杯在这种视觉环境中是突出和显眼的，不由自主地引起人们的注意。所以我们会把视力最敏锐的地方放到咖啡上。
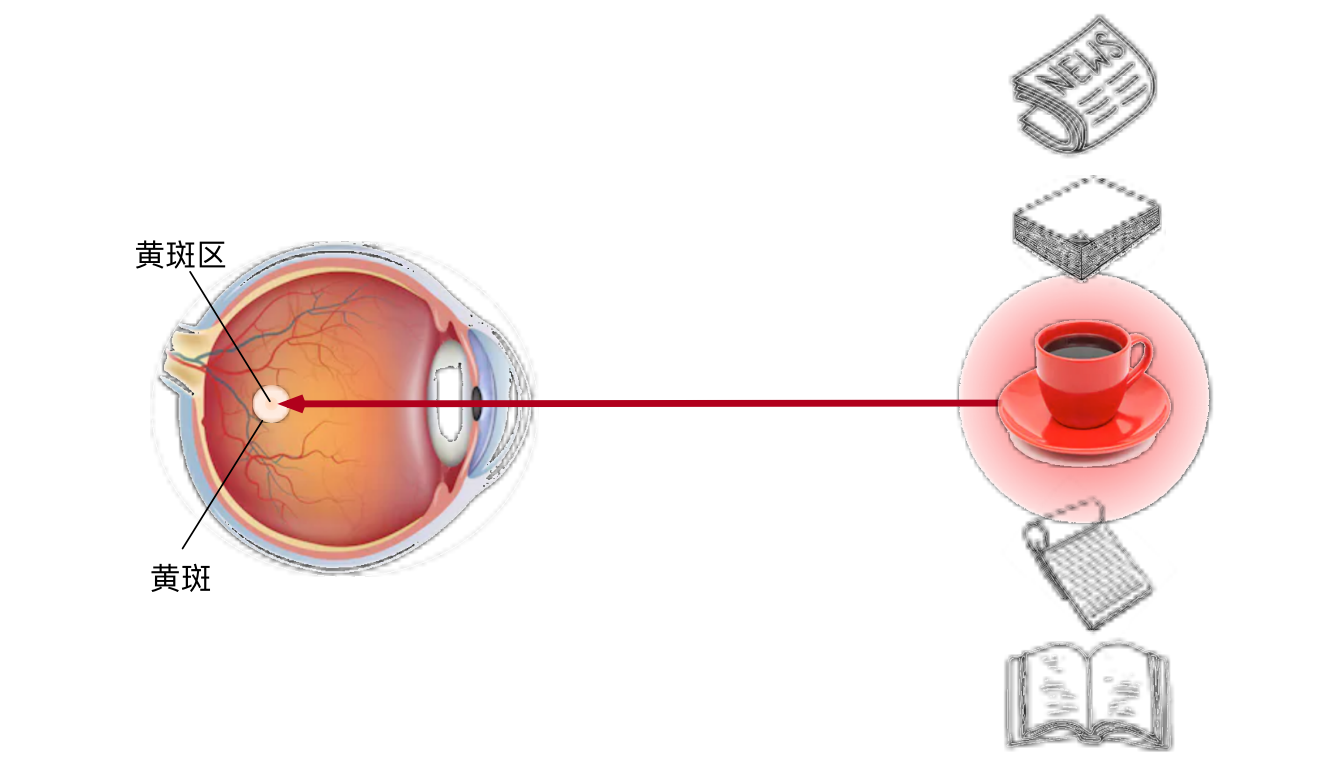
image
喝咖啡后，我们会变得兴奋并想读书，所以转过头，重新聚焦眼睛，然后看看书，就像下图中描述那样。与上图中由于突出性导致的选择不同，此时选择书是受到了认知和意识的控制，因此注意力在基于自主性提示去辅助选择时将更为谨慎。受试者的主观意愿推动，选择的力量也就更强大。
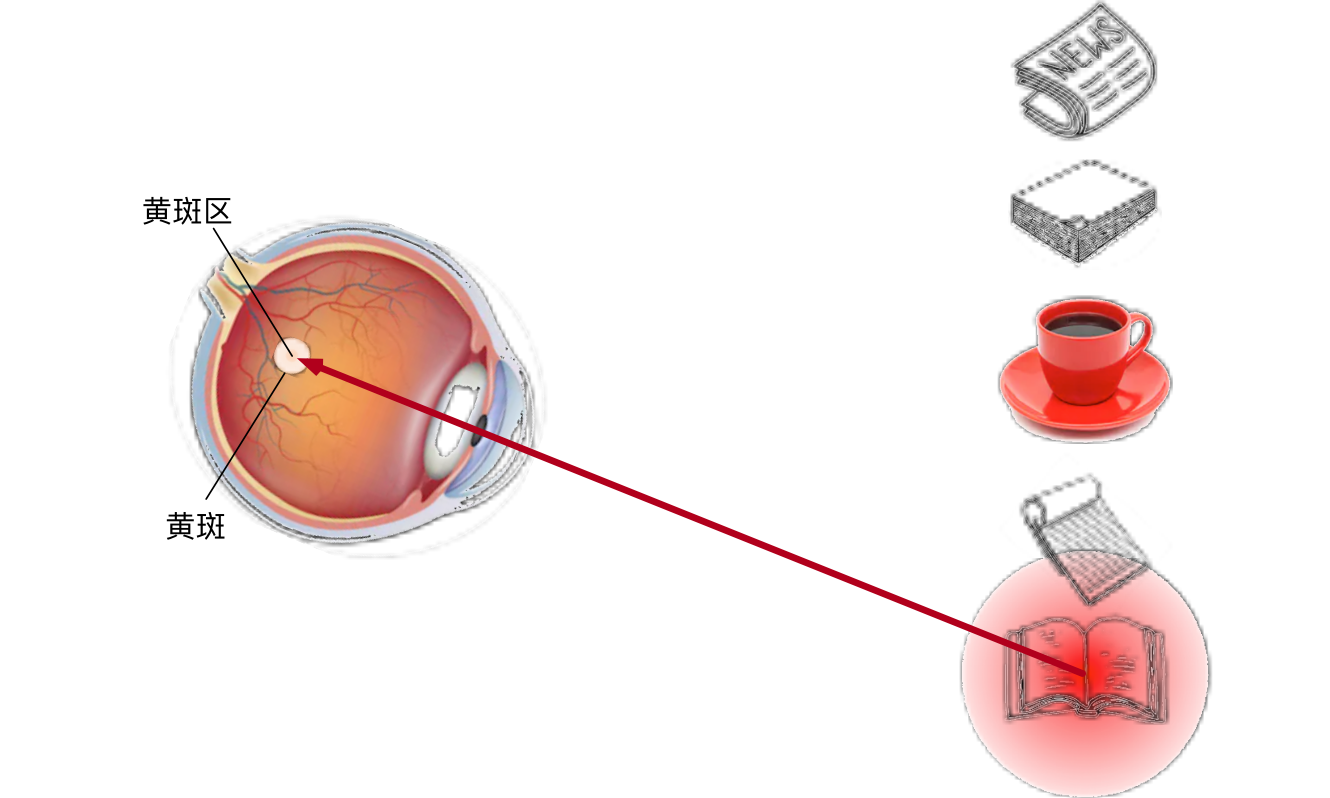
image
在当前计算机算力资源的限制下，注意力机制绝对是提高效率的一种必要手段，将注意力集中在有用的信息上，不要在噪声中花费时间

查询、键和值

自主性的与非自主性的注意力提示解释了人类的注意力的方式，下面来看看如何通过这两种注意力提示，用神经网络来设计注意力机制的框架。
首先，考虑一个相对简单的状况，即只使用非自主性提示。要想将选择偏向于感官输入，则可以简单地使用参数化的全连接层，甚至是非参数化的最大汇聚层或平均汇聚层。
因此，“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。在注意力机制的背景下，自主性提示被称为查询（query）。给定任何查询，注意力机制通过注意力汇聚（attention pooling）将选择引导至感官输入（sensory inputs，例如中间特征表示）。在注意力机制中，这些感官输入被称为值（value）。更通俗的解释，每个值都与一个键（key）配对，这可以想象为感官输入的非自主提示。如下图所示，可以通过设计注意力汇聚的方式，便于给定的查询（自主性提示）与键（非自主性提示）进行匹配，这将引导得出最匹配的值（感官输入）。
image
其中q代表这个query,后续会去和每一个k进行匹配，k代表这个key,后续会被每一个q匹配，v代表从中提取得到的信息。后续q和k匹配的过程可以理解成计算两者的相关性，相关性越大对应v的权重也就越大。
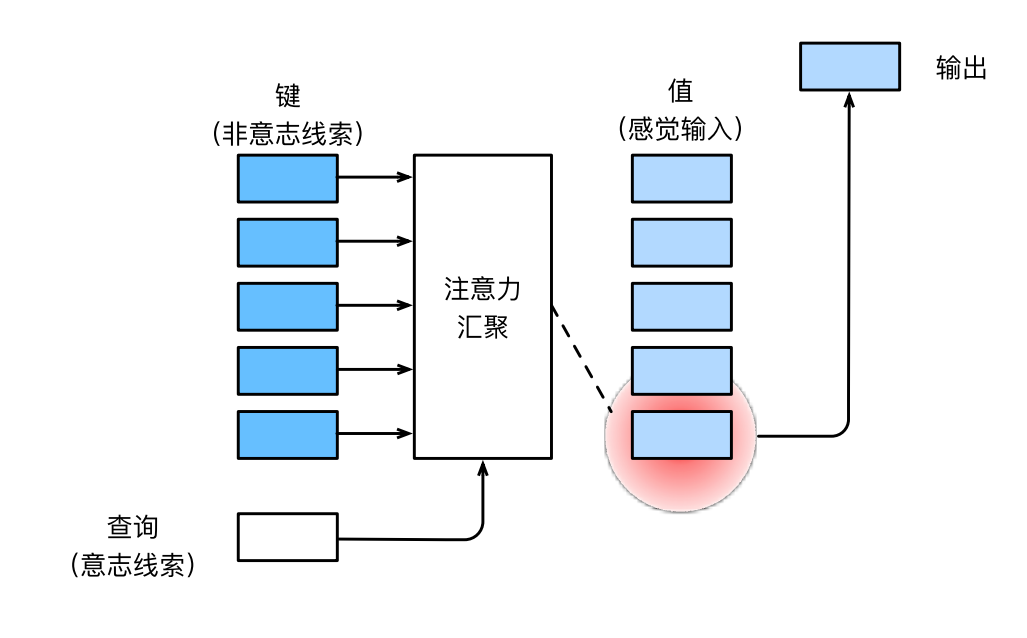
image
注意力机制就是从众多信息中选择出对当前任务目标更关键的信息将注意力放在这上面。

注意力汇聚：Nadaraya-Watson 核回归

上节介绍了框架下的注意力机制的主要成分：查询（自主提示）和键（非自主提示）之间的交互形成了注意力汇聚；注意力汇聚有选择地聚合了值（感官输入）以生成最终的输出。本节将介绍注意力汇聚的更多细节，以便从宏观上了解注意力机制在实践中的运作方式。具体来说，1964年提出Nadaraya‐Watson核回归模型是一个简单但完整的例子，可以用于演示具有注意力机制的机器学习。

import torch
from torch import nn
from d2l import torch as d2l

生成数据集

简单起见，考虑下面这个回归问题：给定的成对的“输入－输出”数据集 \({(x_1, y_1), . . . ,(x_n, y_n)}\)，如何学习\(f\)来预测任意新输入\(x\)的输出\(\widehat {y} = f(x)\)？
根据下面的非线性函数生成一个人工数据集，其中加入的噪声项为\(\varepsilon\)：

\[y_i = 2sin(x_i) + x^{0.8}_i + \varepsilon \]

其中\(\varepsilon\)服从均值为0和标准差为0.5的正态分布。在这里生成了50个训练样本和50个测试样本。为了更好地可视化之后的注意力模式，需要将训练样本进行排序。

n_train = 50 # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5) # 排序后的训练样本

def f(x):
    return 2 * torch.sin(x) + x**0.8

y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出
x_test = torch.arange(0, 5, 0.1) # 测试样本
y_truth = f(x_test)# 测试样本的真实输出
n_test = len(x_test)# 测试样本数
n_test

下面的函数将绘制所有的训练样本（样本由圆圈表示），不带噪声项的真实数据生成函数f（标记为“Truth”），以及学习得到的预测函数（标记为“Pred”）。

def plot_kernel_reg(y_hat):
    d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],
             xlim=[0, 5], ylim=[-1, 5])
    d2l.plt.plot(x_train, y_train, 'o', alpha=0.5);

平均汇聚

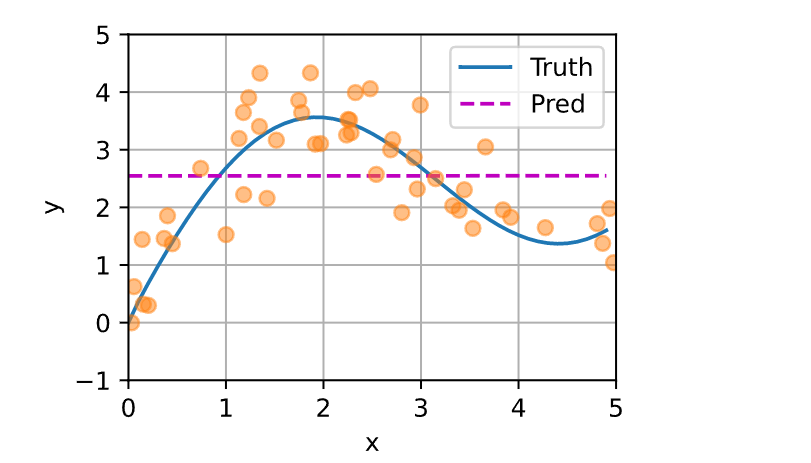
先使用最简单的估计器来解决回归问题。基于平均汇聚来计算所有训练样本输出值的平均值：

\[f(x) = \frac{1}{n}\sum_{i=1}^n{y_i} \]

y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)

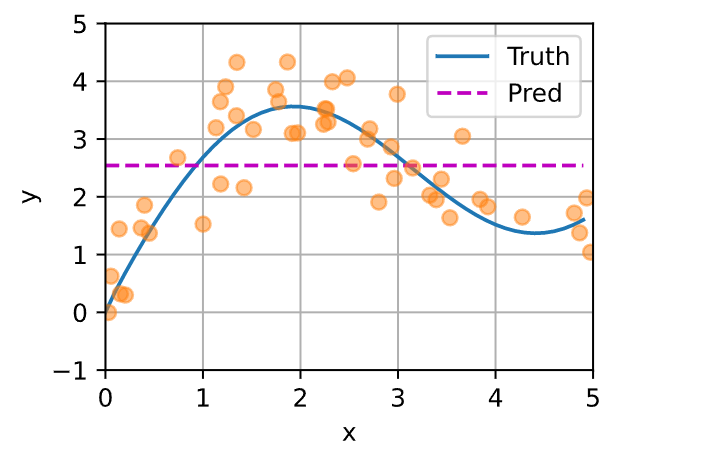
image

非参数注意力汇聚

显然，平均汇聚忽略了输入\(x_i\)。于是Nadaraya (Nadaraya, 1964)和 Watson (Watson, 1964)提出了一个更好的想法，根据输入的位置对输出\(y_i\)进行加权：

\[f(x) = \sum_{i=1}^n \frac{K(x − x_i)}{\sum_{j=1}^n K(x − x_j)}y_i \]

其中K是核（kernel）。公式所描述的估计器被称为 Nadaraya-Watson核回归。这里不会深入讨论核函数的细节，但受此启发，我们可以注意力机制框架的角度重写，成为一个更加通用的注意力汇聚公式：

\[f(x) = \sum_{i=1}^nα(x, x_i)y_i, \]

其中x是查询，\((x_i, y_i)\)是键值对。比较上面两个公式，注意力汇聚是\(y_i\)的加权平均。将查询\(x\)和键\(x_i\)之间的关系建模为注意力权重\(α(x, x_i)\)，如上面公式所示，这个权重将被分配给每一个对应值\(y_i\)。对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布：它们是非负的，并且总和为1。
为了更好地理解注意力汇聚，下面考虑一个高斯核（Gaussian kernel），其定义为：

\[K(u)=\frac{1}{\sqrt{2\pi}}exp(-\frac{u^2}{2}) \]

将高斯核代入：
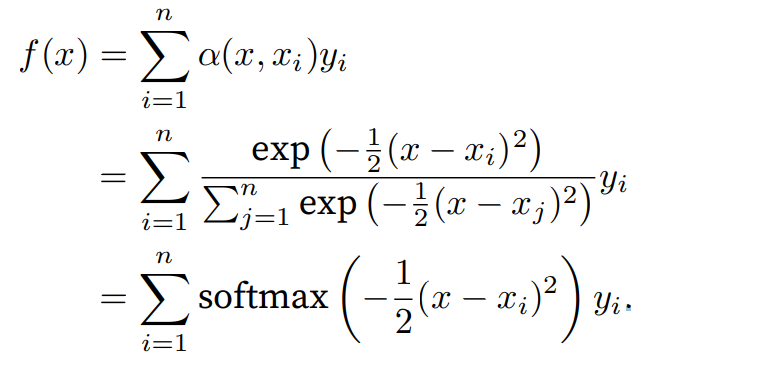
image
如果一个键\(x_i\)越是接近给定的查询\(x\)，那么分配给这个键对应值\(y_i\)的注意力权重就会越大，也就“获得了更多的注意力”。值得注意的是，Nadaraya‐Watson核回归是一个非参数模型。因此，是非参数的注意力汇聚模型。接下来，我们将基于这个非参数的注意力汇聚模型来绘制预测结果。从绘制的结果会发现新的模型预测线是平滑的，并且比平均汇聚的预测更接近真

# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入（例如：同样的查询）
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
# x_train包含着键。attention_weights的形状：(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值（y_train）之间分配的注意力权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值，其中的权重是注意力权重
y_hat = torch.matmul(attention_weights, y_train)
plot_kernel_reg(y_hat)

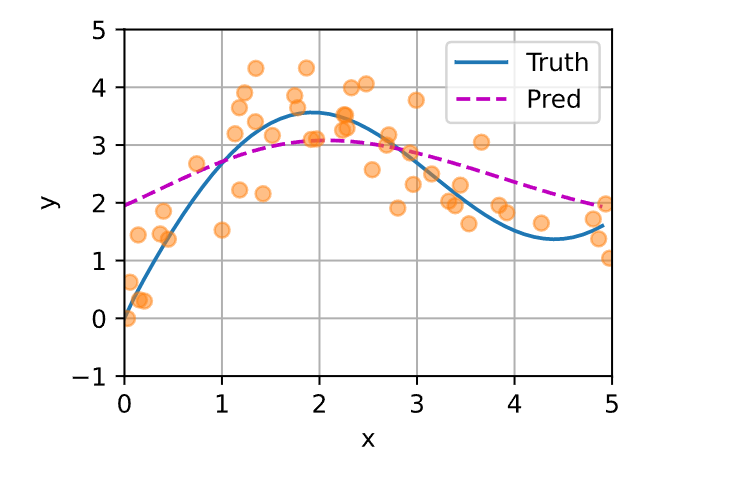
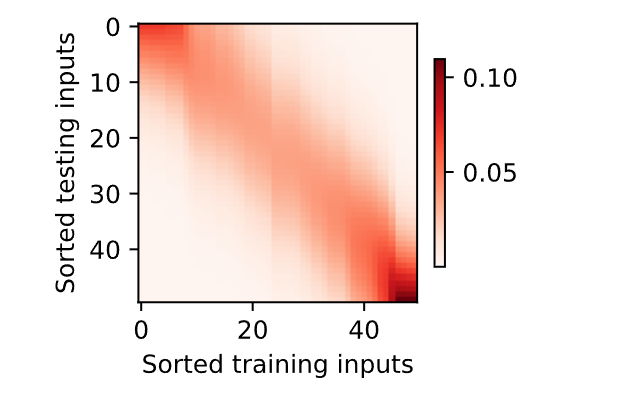
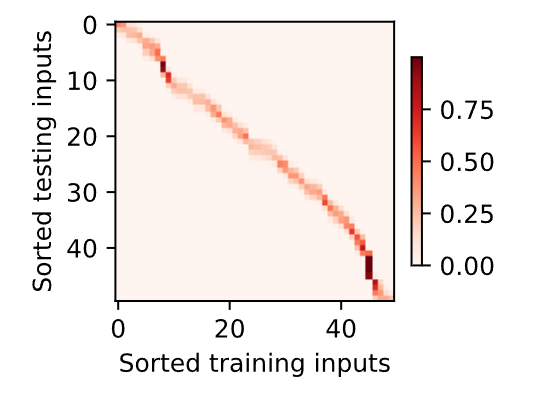
image
现在来观察注意力的权重。这里测试数据的输入相当于查询，而训练数据的输入相当于键。因为两个输入都是经过排序的，因此由观察可知“查询‐键”对越接近，注意力汇聚的注意力权重就越高。

d2l.show_heatmaps(
    attention_weights.unsqueeze(0).unsqueeze(0),
    xlabel='Sorted training inputs', ylabel='Sorted testing inputs')

image
非参数的Nadaraya‐Watson核回归具有一致性（consistency）的优点：如果有足够的数据，此模型会收敛到最优结果。尽管如此，我们还是可以轻松地将可学习的参数集成到注意力汇聚中。
例如，与上式略有不同，在下面的查询\(x\)和键\(x_i\)之间的距离乘以可学习参数\(w\)：
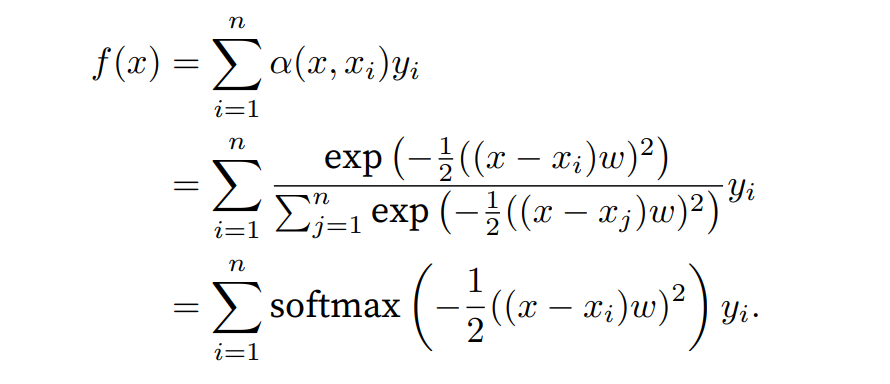
image
本节的余下部分将通过训练这个模型来学习注意力汇聚的参

批量矩阵乘法

为了更有效地计算小批量数据的注意力，我们可以利用深度学习开发框架中提供的批量矩阵乘法。假设第一个小批量数据包含\(n\)个矩阵\(X_1, . . . , X_n\)，形状为\(a × b\)，第二个小批量包含\(n\)个矩阵\(Y1, . . . , Yn\)，形状为\(b × c\)。它们的批量矩阵乘法得到n个矩阵\(X_1Y_1, . . . ,X_nY_n\)，形状为\(a × c\)。因此，假定两个张量的形状分别是(n, a, b)和(n, b, c)，它们的批量矩阵乘法输出的形状为(n, a, c)。

X = torch.ones((2, 1, 4))
Y = torch.ones((2, 4, 6))
torch.bmm(X, Y).shape

# torch.Size([2, 1, 6])

在注意力机制的背景中，我们可以使用小批量矩阵乘法来计算小批量数据中的加权平均值。

weights = torch.ones((2, 10)) * 0.1
values = torch.arange(20.0).reshape((2, 10))
torch.bmm(weights.unsqueeze(1), values.unsqueeze(-1))

# tensor([[[ 4.5000]],
#         [[14.5000]]])

weights,values

image

定义模型

基于带参数的注意力汇聚，使用小批量矩阵乘法，定义Nadaraya‐Watson核回归的带参数版本为：

class NWKernelRegression(nn.Module):
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.w = nn.Parameter(torch.rand((1,), requires_grad=True))

    def forward(self, queries, keys, values):
        # queries和attention_weights的形状为(查询个数，“键－值”对个数)
        queries = queries.repeat_interleave(keys.shape[1]).reshape(
            (-1, keys.shape[1]))
        self.attention_weights = nn.functional.softmax(
            -((queries - keys) * self.w)**2 / 2, dim=1)
        # values的形状为(查询个数，“键－值”对个数)
        return torch.bmm(self.attention_weights.unsqueeze(1),
                         values.unsqueeze(-1)).reshape(-1)

训练

接下来，将训练数据集变换为键和值用于训练注意力模型。在带参数的注意力汇聚模型中，任何一个训练样本的输入都会和除自己以外的所有训练样本的“键－值”对进行计算，从而得到其对应的预测输出。

net = NWKernelRegression()
loss = nn.MSELoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
#animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])

for epoch in range(5):
    trainer.zero_grad()
    l = loss(net(x_train, keys, values), y_train) / 2
    l.sum().backward()
    trainer.step()
   # animator.add(epoch + 1, float(l.sum()))
    print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')

epoch 1, loss 33.963810
epoch 2, loss 33.946701
epoch 3, loss 33.953354
epoch 4, loss 33.956551
epoch 5, loss 33.955387

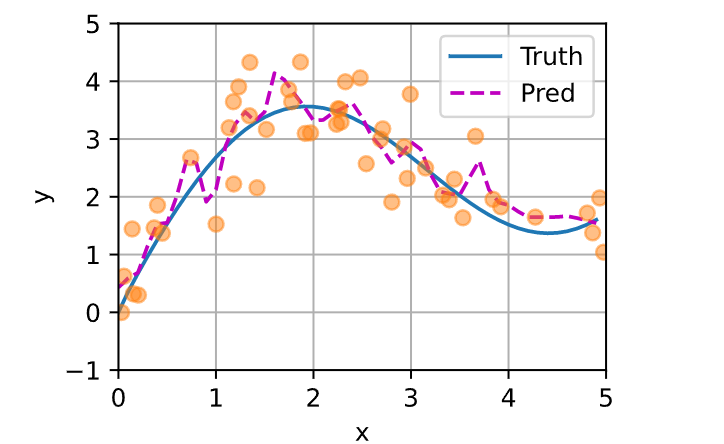
如下所示，训练完带参数的注意力汇聚模型后可以发现：在尝试拟合带噪声的训练数据时，预测结果绘制的线不如之前非参数模型的平滑。

# keys的形状:(n_test，n_train)，每一行包含着相同的训练输入（例如，相同的键）
keys = x_train.repeat((n_test, 1))
# value的形状:(n_test，n_train)
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
plot_kernel_reg(y_hat)

image
为什么新的模型更不平滑了呢？下面看一下输出结果的绘制图：与非参数的注意力汇聚模型相比，带参数的模型加入可学习的参数后，曲线在注意力权重较大的区域变得更不平滑。

# keys的形状:(n_test，n_train)，每一行包含着相同的训练输入（例如，相同的键）
keys = x_train.repeat((n_test, 1))
# value的形状:(n_test，n_train)
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
plot_kernel_reg(y_hat)

image
为什么新的模型更不平滑了呢？下面看一下输出结果的绘制图：与非参数的注意力汇聚模型相比，带参数的模型加入可学习的参数后，曲线在注意力权重较大的区域变得更不平滑。

d2l.show_heatmaps(
    net.attention_weights.unsqueeze(0).unsqueeze(0),
    xlabel='Sorted training inputs', ylabel='Sorted testing inputs')

image
• Nadaraya‐Watson核回归是具有注意力机制的机器学习范例。
• Nadaraya‐Watson核回归的注意力汇聚是对训练数据中输出的加权平均。从注意力的角度来看，分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。
• 注意力汇聚可以分为非参数型和带参数型。

Encoder-Decoder框架理解来理解注意力机制

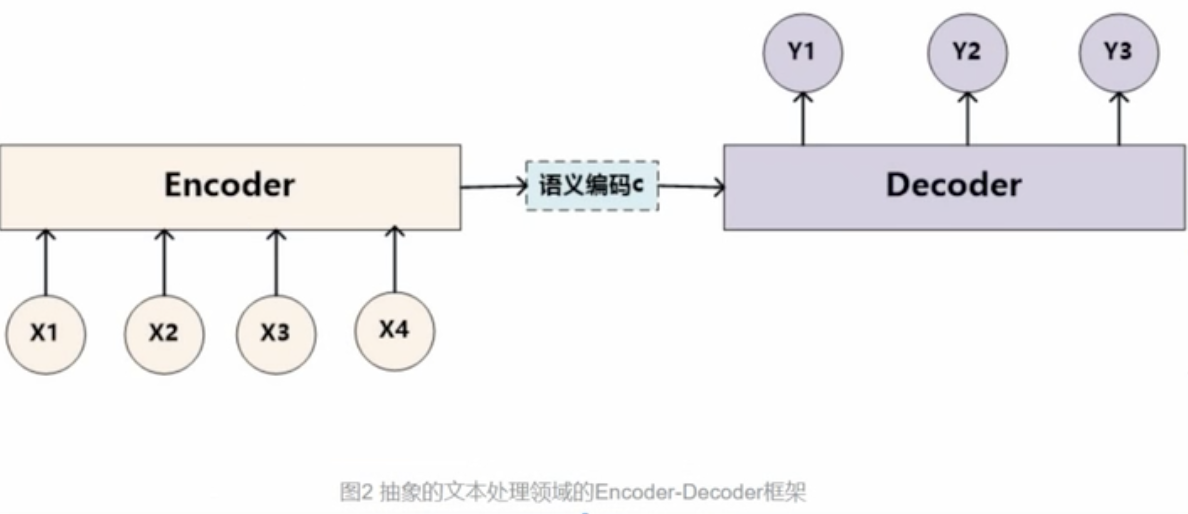
image
对于这个Encoder部分，这个文本处理和语音识别的Encoder部分通常采用RNN模型，图像处理的Encoder一般采用CNN模型。我们思考这样一个场景：输入的是英文句子：Tom chase Jerry翻译生成中文单词：“汤姆”，“追逐”，“杰瑞”。其中它的信息是"Tom chase Jerry"，每次生成一个目标单词，每个目标单词的有效信息都不一样，比如对于“杰瑞”，最重要的信息应该是“Jerry”。

分心模型

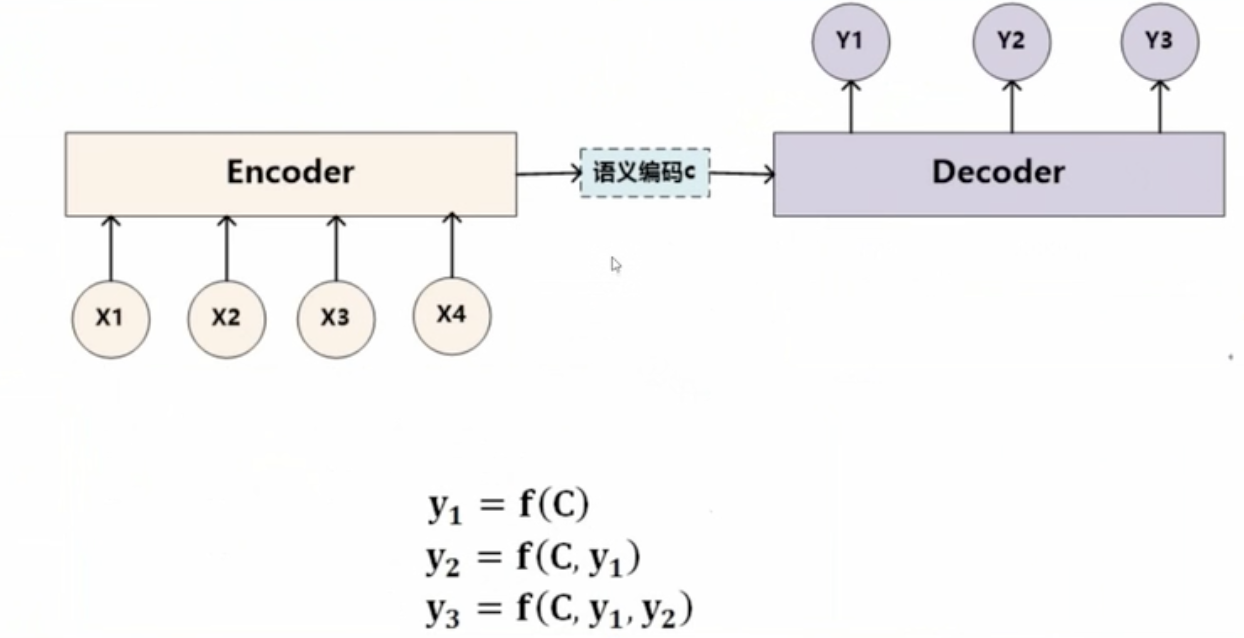
image
在翻译“杰瑞”时，“Tom”，“chase”，“Jerry”三者贡献的注意力是一样的。

注意力机制

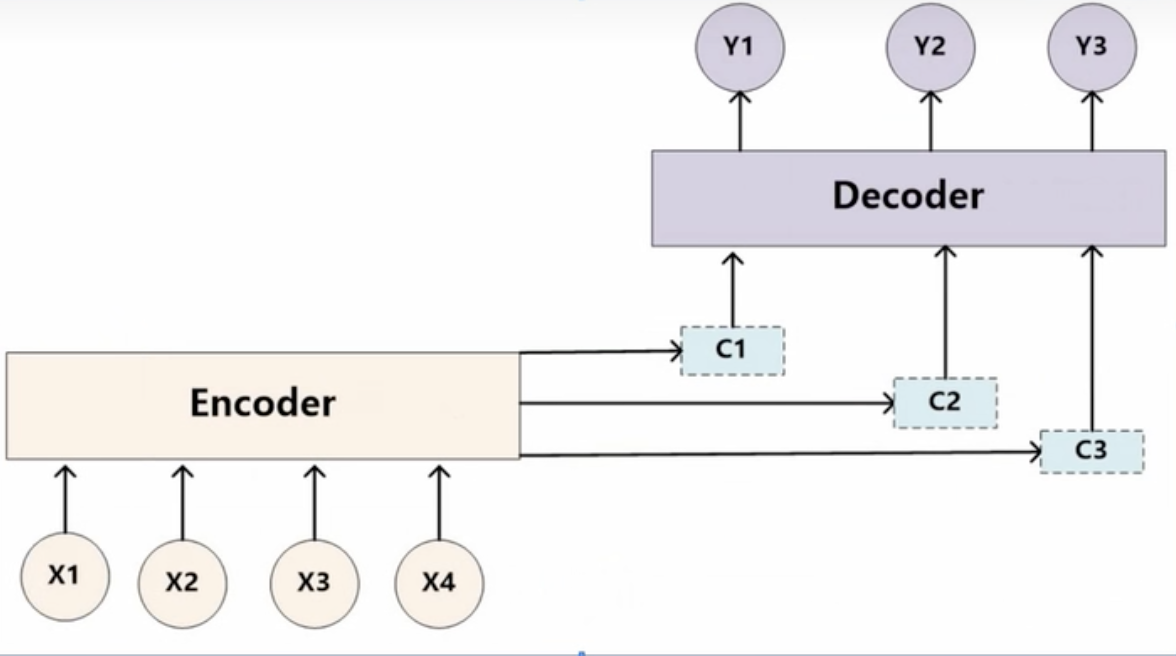
image
在引入注意力机制之后，语义编码\(c\)变成\(c_1\)，\(c_2\)，\(c_3\)，此时\(c\)的作用就是：如\(c_1\)，他的意思就是哪一个和\(Y_1\)（Tom）更相关。也就是来筛选掉有效的信息，也就是降低无效的信息的比重。然后就是他这个\(C_i\)是怎么生成的呢？
对于每个\(C\)可能对应这个不同的源语句子单词的注意力分配概率分布，比如对于上面的英汉翻译来说：其对应的信息如下：

\[C_{汤姆}=g(0.6*f_2(Tom),0.2*f_2(chase),0.2*f_2(Jerry)) \]

\[C_{追逐}=g(0.2*f_2(Tom),0.7*f_2(chase),0.1*f_2(Jerry)) \]

\[C_{杰瑞}=g(0.3*f_2(Tom),0.2*f_2(chase),0.5*f_2(Jerry)) \]

其中g函数就是对构成元素加权求和:\(C_i=\sum_{i=1}^{L_x}a_{ij}h_i\)
image

Attention机制的本质思想与具体计算过程

从概念上理解，把Attention仍然理解为从大量信息中有选择的筛选出少量重要信息并聚焦到这些重要信息上，忽略大多不重要的信息。
其实它的具体计算过程可以概况成这一幅图：
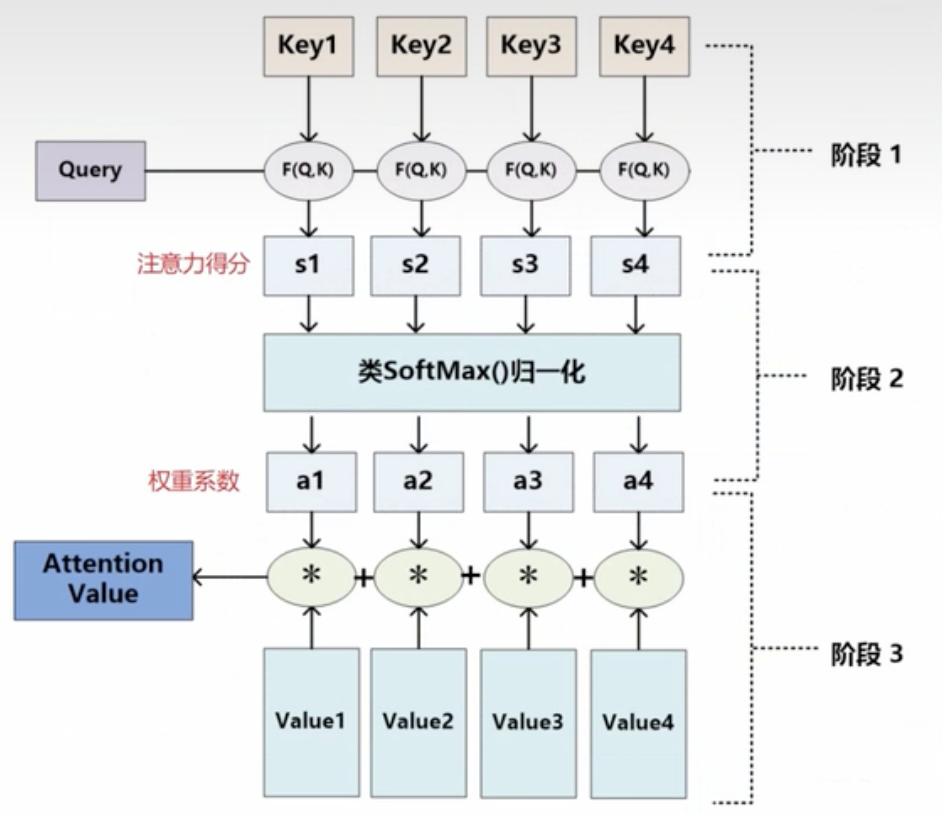
image
1.根据Query和Key计算两者的相似度或者相关
其中第一步就是先计算相关性：例如这个Query是Tom，然后我们分别计算Tom和“Tom”，“chase”，“Jerry”,这三个的相关性。在计算相似性的时候，我们可以引入不同的函数和计算机制，根据Query和某个key（这里，每一个q都需要和所有key计算），计算两者的相似度和相关性。其中常见的方法：
image
不同的计算函数\(F\)也就对应了不同的Attention。然后我们通过F函数计算，就得到了一个注意力得分，也就是它的相似度的得分。得分越高它的相似度也就越大。

2.对上一步进行softmax归一化处理
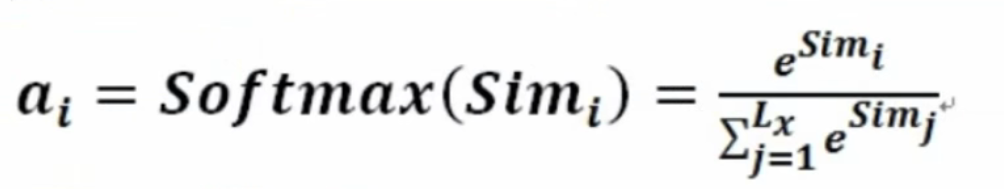
image
然后就得到了一个0到1之间的权重系数\(a_1\),\(a_2\),\(a_3\),\(a_4\)。

3.根据权重系数对value进行加权求和
也就是说\(a_1*value_1+a_2*value_2+a_3*value_3+a_4*value_4=>Attention Value\).
对于这里value和key其实是一个东西。
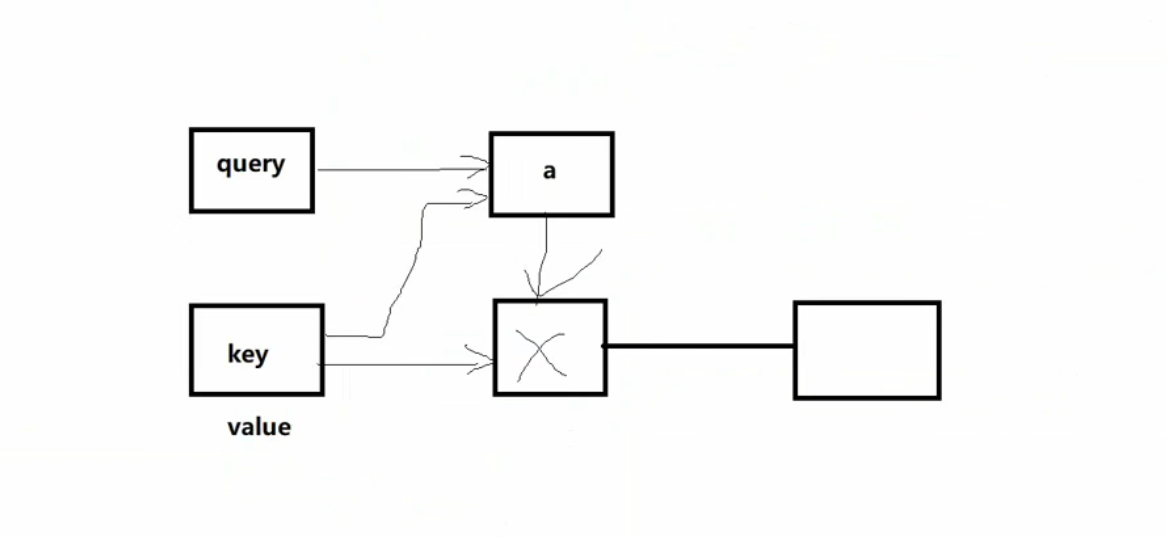
image
目前绝大多数具体的注意力机制计算方法，都符合上述的三阶段。

其实上面讲的核方法中的：
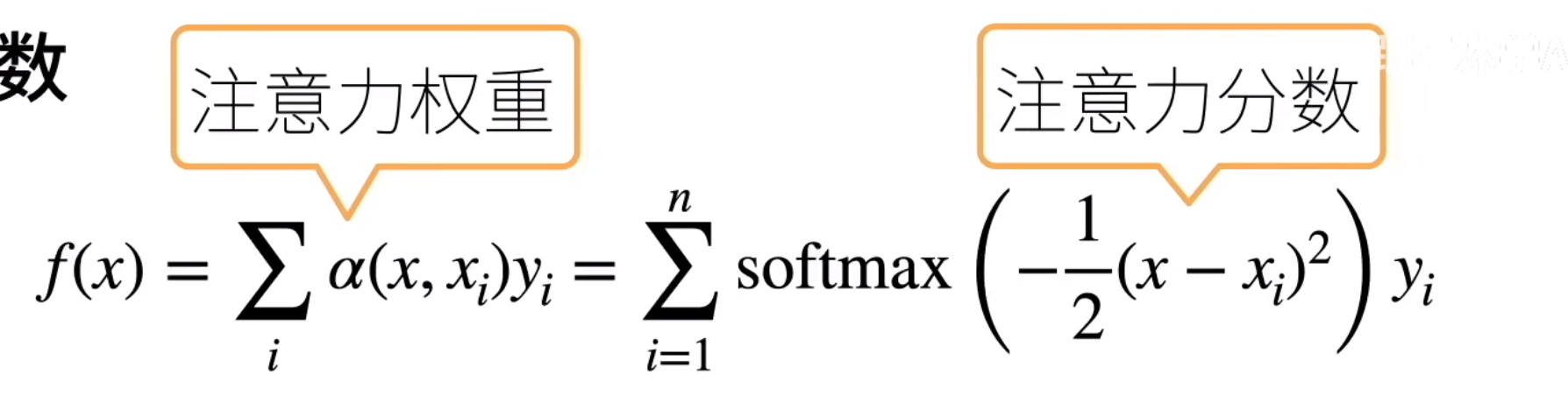
image
这个个f就是来算注意力得分的。其实这里面的注意力分数可以理解为相似度。

posted @ 2023-09-11 19:43  lipu123  阅读(244)  评论(0)    收藏  举报