深度循环神经网络

到目前为止，我们只讨论了具有⼀个单向隐藏层的循环神经网络。其中，隐变量和观测值与具体的函数形式的交互方式是相当随意的。只要交互类型建模具有足够的灵活性，这就不是⼀个大问题。然而，对⼀个单层来说，这可能具有相当的挑战性。之前在线性模型中，我们通过添加更多的层来解决这个问题。而在循环神经网络中，我们首先需要确定如何添加更多的层，以及在哪里添加额外的非线性，因此这个问题有点棘手。
事实上，我们可以将多层循环神经网络堆叠在⼀起，通过对几个简单层的组合，产生了⼀个灵活的机制。特别是，数据可能与不同层的堆叠有关。
下图描述了⼀个具有L个隐藏层的深度循环神经网络，每个隐状态都连续地传递到当前层的下⼀个时间步和下⼀层的当前时间步。其中输出是\(O_t\)。

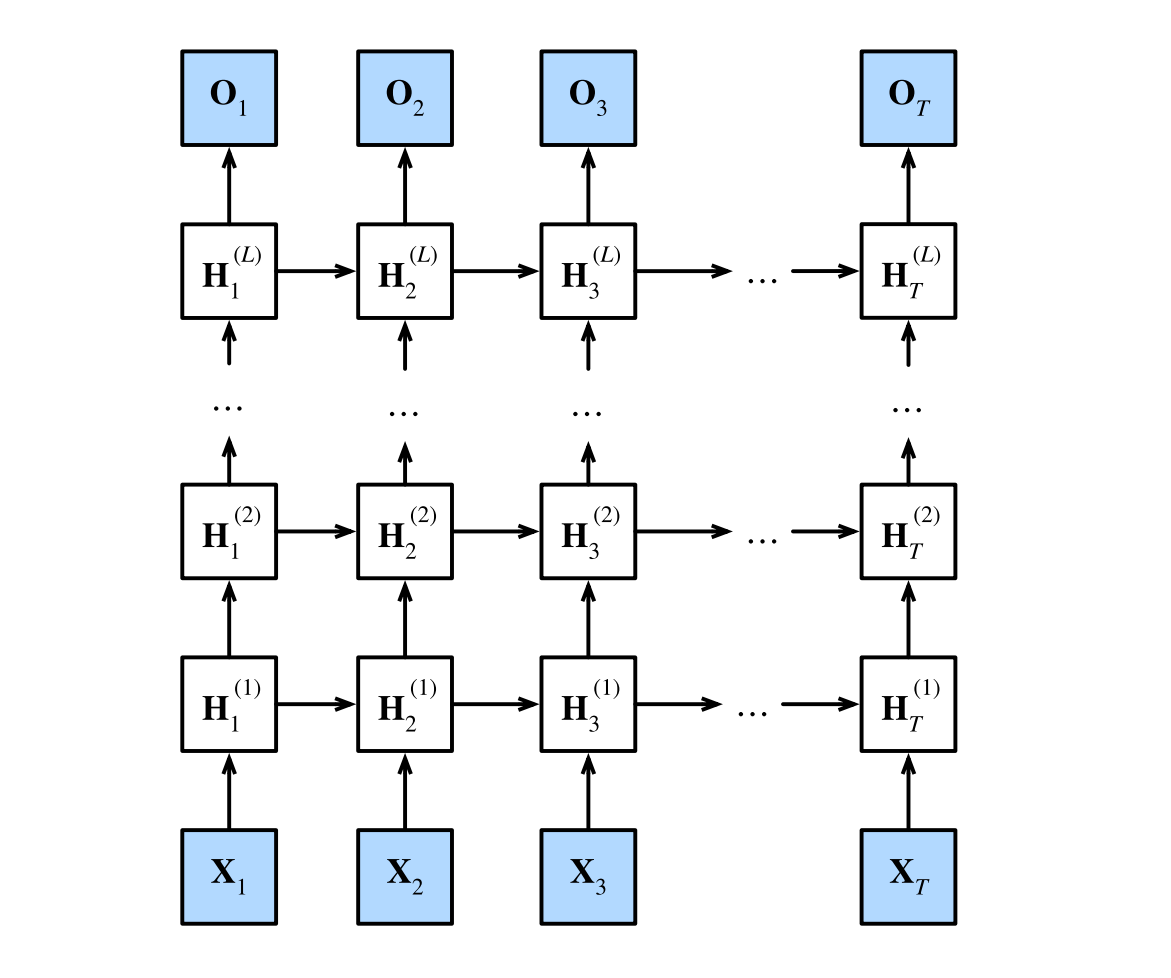
函数依赖关系

我们可以将深度架构中的函数依赖关系形式化，这个架构是由 上图中描述了L个隐藏层构成。后续的讨论主要集中在经典的循环神经网络模型上，但是这些讨论也适应于其他序列模型。
假设在时间步t有⼀个小批量的输入数据\(X_t \in R^{n×d}\)（样本数：\(n\)，每个样本中的输⼊数：\(d\)）。同时，将\(l^{th}\)隐藏层\(（l = 1, . . . , L）\)的隐状态设为\(H^{(l)}_t \in R^{n×h}\)（隐藏单元数：\(h\)），输出层变量设为\(O_t \in R^{n×q}\)（输出数：\(q\)）。设置\(H^(0) _t = X_t\)，第\(l\)个隐藏层的隐状态使用激活函数\(\phi l\)，则：

\[H^{(l)}_t = \phi _l(H6^{(l−1)}_tW^{(l)}_{xh} + H ^{(l)}_{t−1}W^{(l)}_hh + b^{(l)}_h)\]

其中，权重\(W^{(l)}_{xh} \in R^{h×h}\)\(W^{(l)}_{hh} \in R^{h×h}和偏置\)b^{(l)}h \in R$都是第l个隐藏层的模型参数。
最后，输出层的计算仅基于第l个隐藏层最终的隐状态：

\[O_t = H^{(L)}_tW_{hq} + b_q \]

其中，权重\(W_{hq} \in R_{h×q}\)和偏置\(b_q \in R_{1×q}\)都是输出层的模型参数。
与多层感知机一样，隐藏层数目\(L\)和隐藏单元数目\(h\)都是超参数。也就是说，它们可以由我们调整的。另外，用门控循环单元或长短期记忆网络的隐状态来代替\(H^(l)_t\)中的隐状态进行计算，可以很容易地得到深度门控循环神经网络或深度长短期记忆神经网络。

简洁实现

import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

因为我们有不同的词元，所以输⼊和输出都选择相同数量，即vocab_size。隐藏单元的数量仍然是256。唯⼀的区别是，我们现在通过num_layers的值来设定隐藏层数。

vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers)#这个num_layers指的是两层
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)

训练与预测

num_epochs, lr = 500, 2
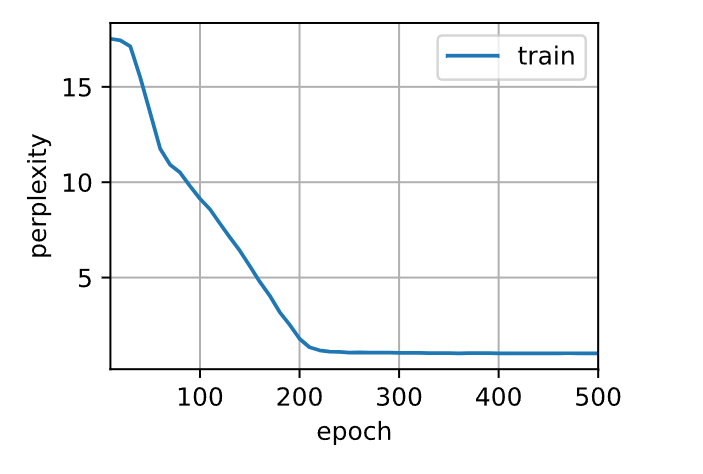
d2l.train_ch8(model, train_iter, vocab, lr*1.0, num_epochs, device)

perplexity 1.0, 138672.1 tokens/sec on cuda:0
time traveller for so it will be convenient to speak of himwas e
traveller with a slight accession ofcheerfulness really thi