pytorch-感知机与多层感知机

感知机

早期1960年的感知机，每一根线就是一个权重。

给定输入x,权重w,和偏移b,感知机输出:

\[o=\sigma(<w,x>+b),\sigma(x)=\begin{split} \begin{cases} 1 & if(x>0)\\ 0 &otherwise\\ \end{cases}\end{split}\]

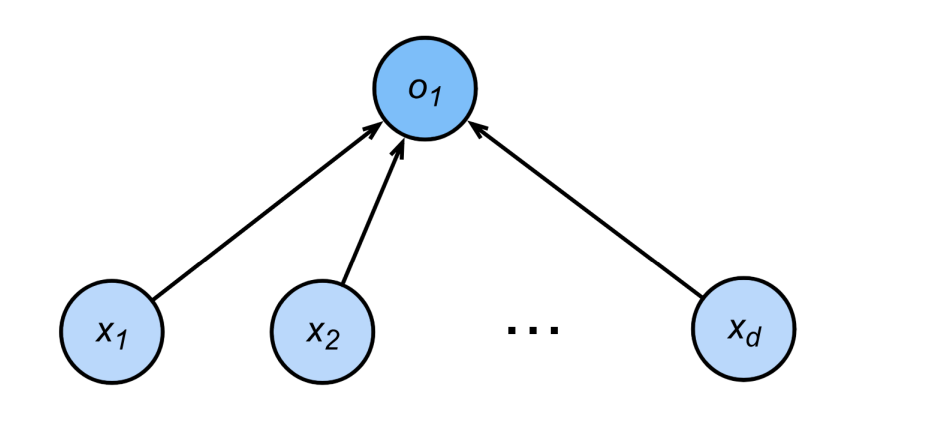
他一般运用于二分类-1或者1

训练感知机

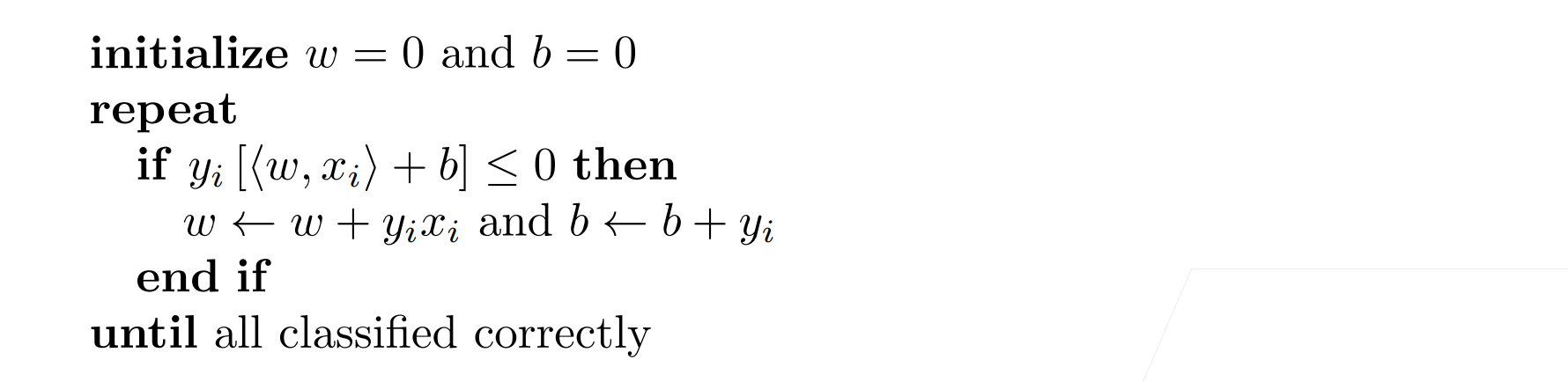
等价于使用批量大小为1的梯度下降，并使用如下损失函数

\[l(y,x,w)=max(0,-y<w,x>) \]

其实它的原理就是：




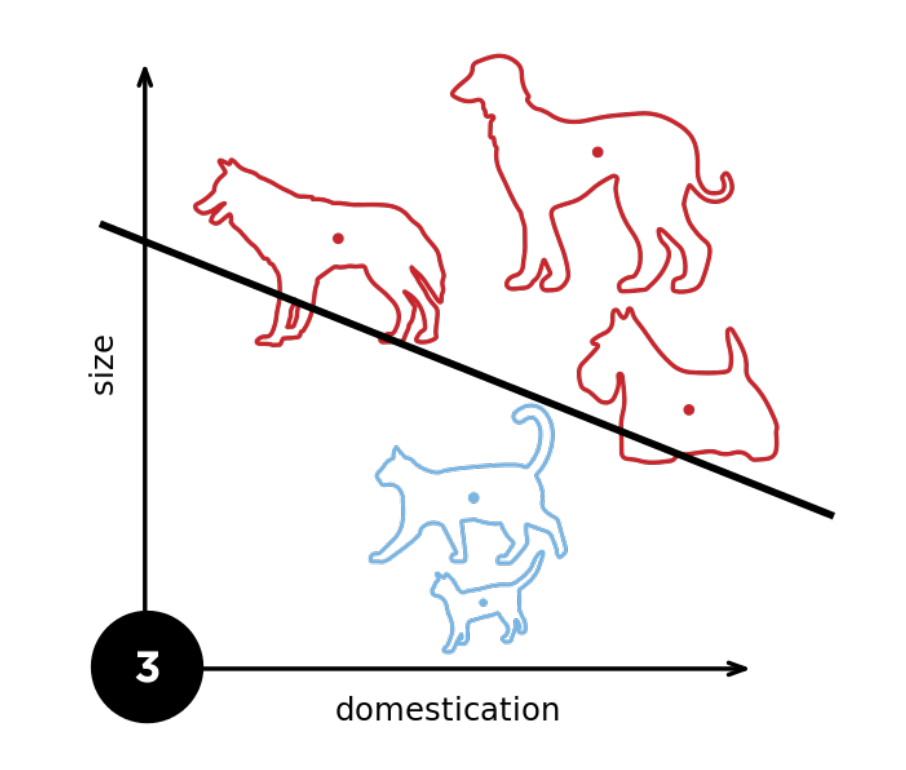
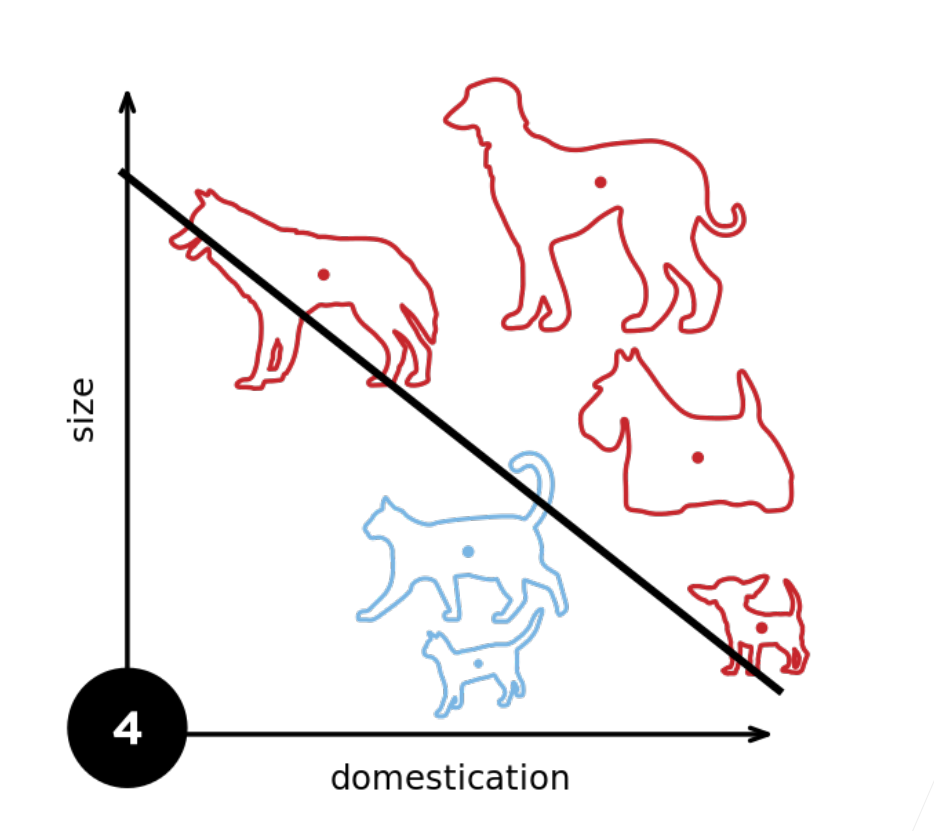
我们增加一个样本他就改变一下他的权重。

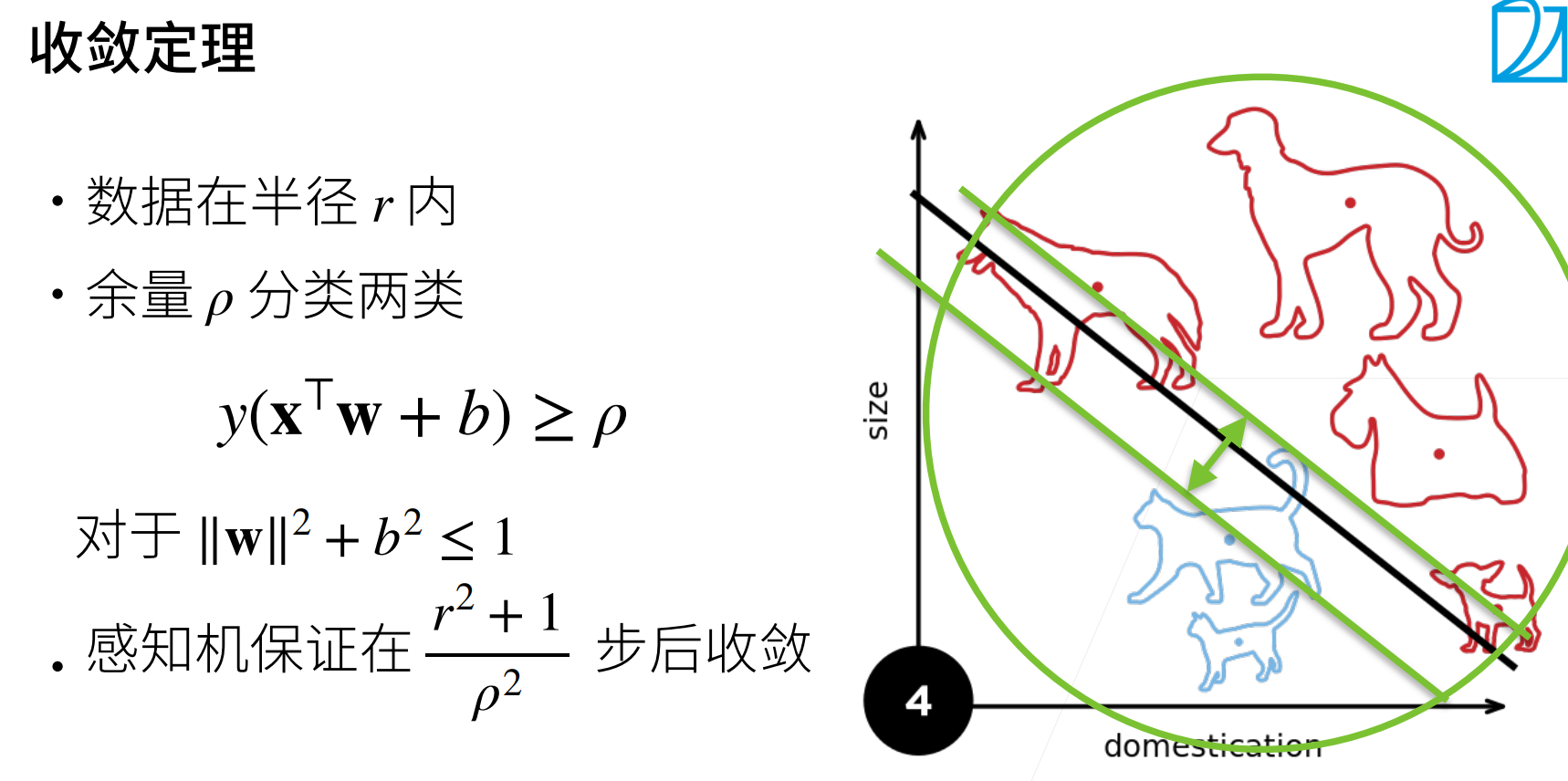
收敛定理

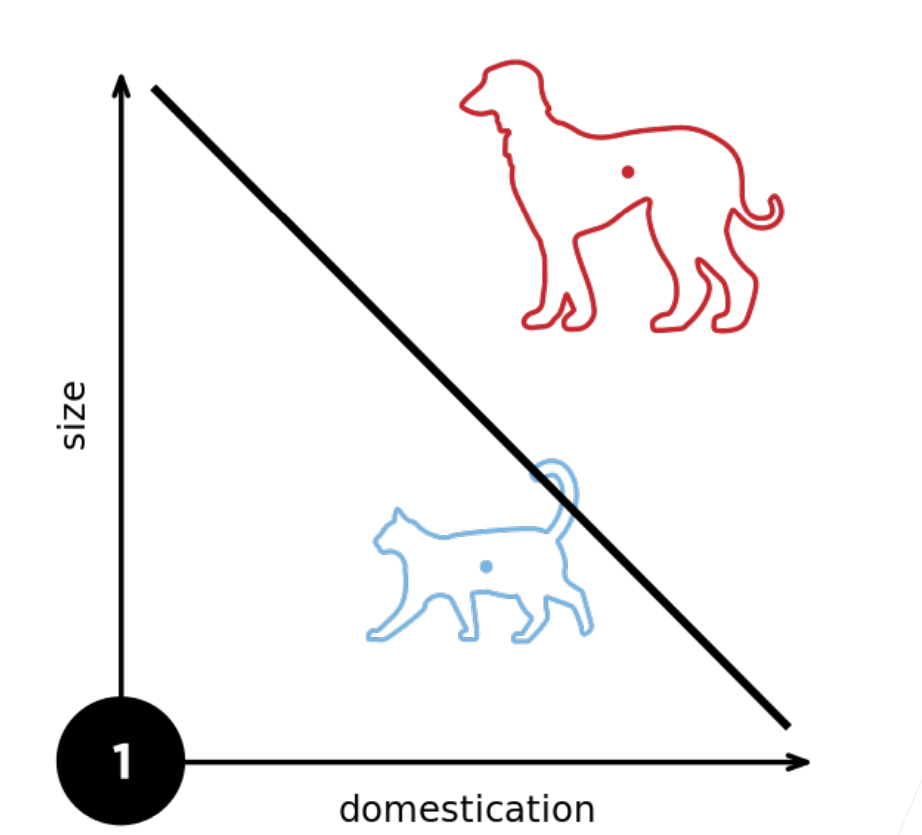
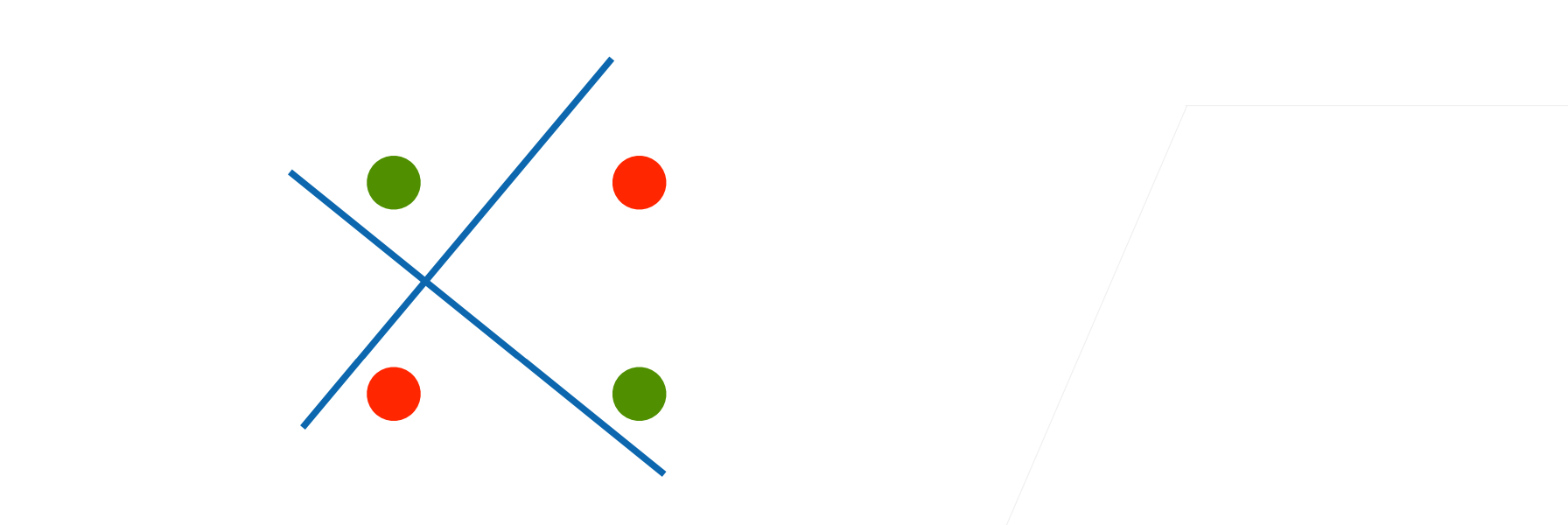
存在问题（XOR问题）

我们发现这个感知机他不能拟合一个很简单的XOR函数，它只能产生线性分割面

总结
·感知机是一个二分类模型，是最早的AI模型之一
·它的求解算法等价于使用批量大小为l的梯度下降
·它不能拟合XOR函数，导致的第一次AI寒冬

多层感知机

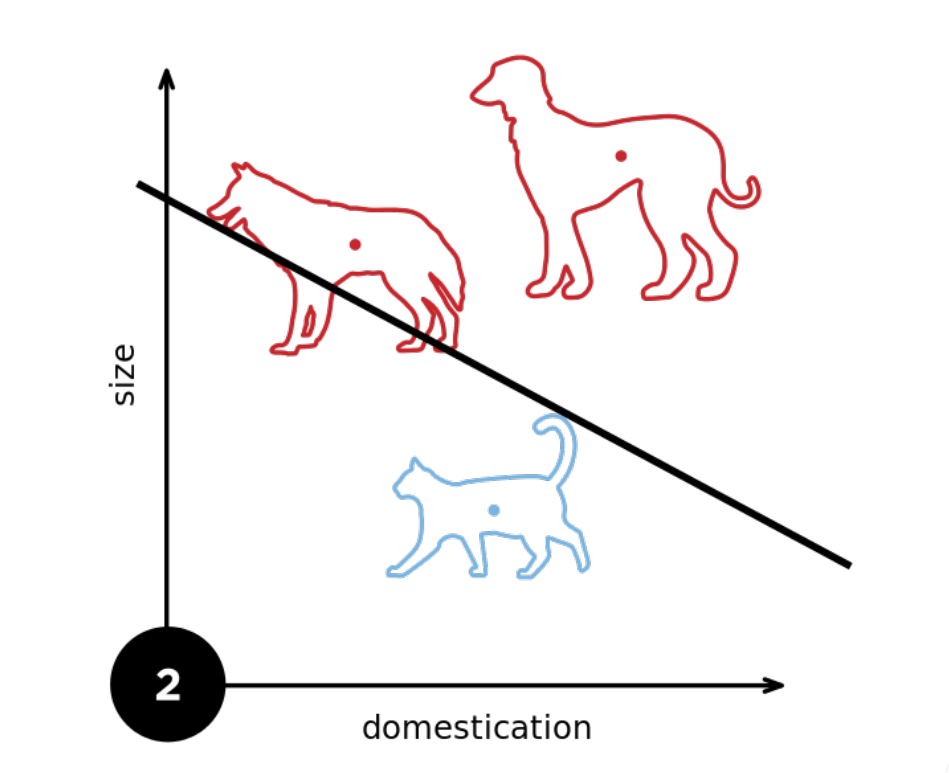
解决XOR问题

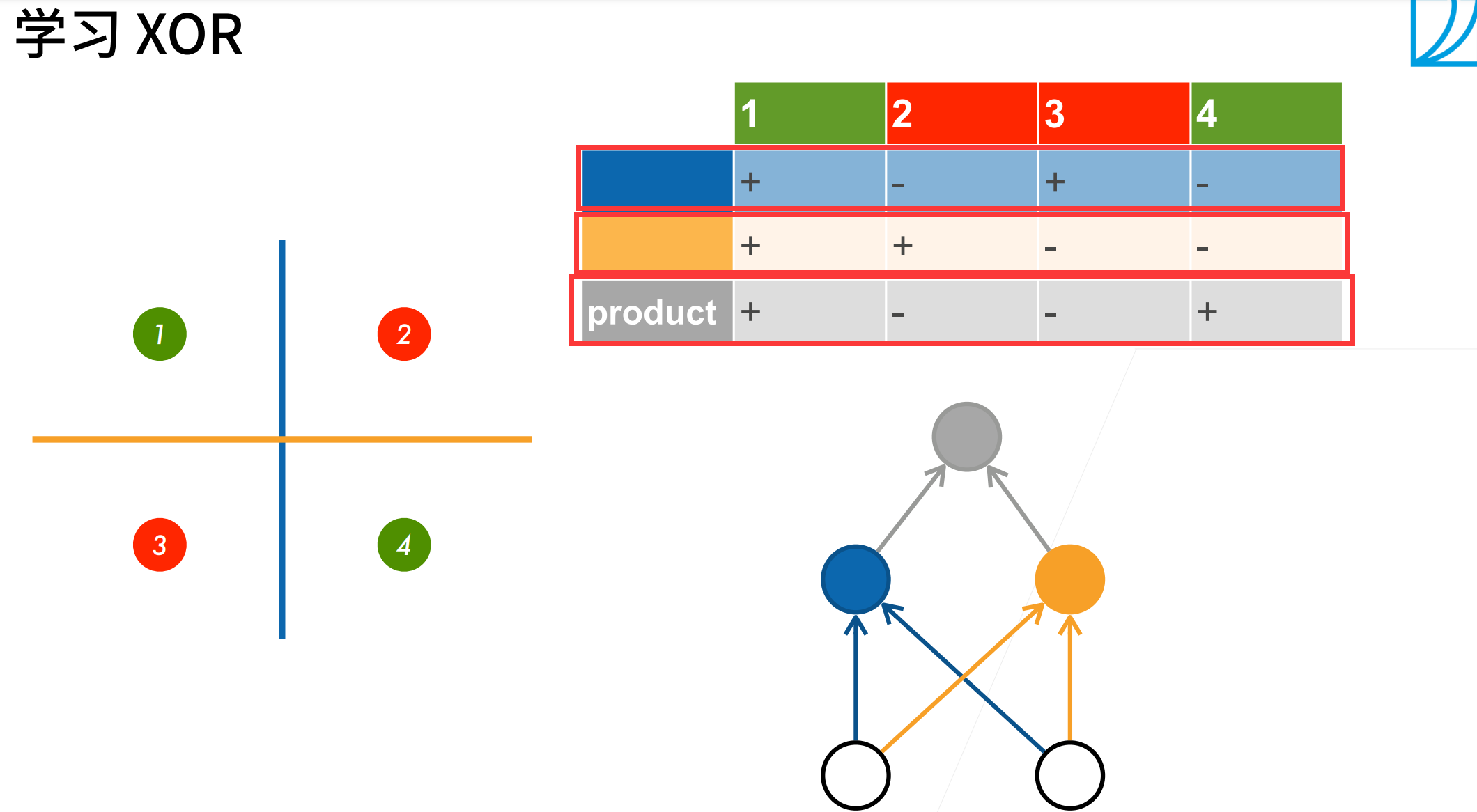
第一步，我们先学习一个蓝色的这个线，第二步，我们在学习一个黄色的线，然后我们根据这两个分类结果，得到总的结果。

单隐藏层

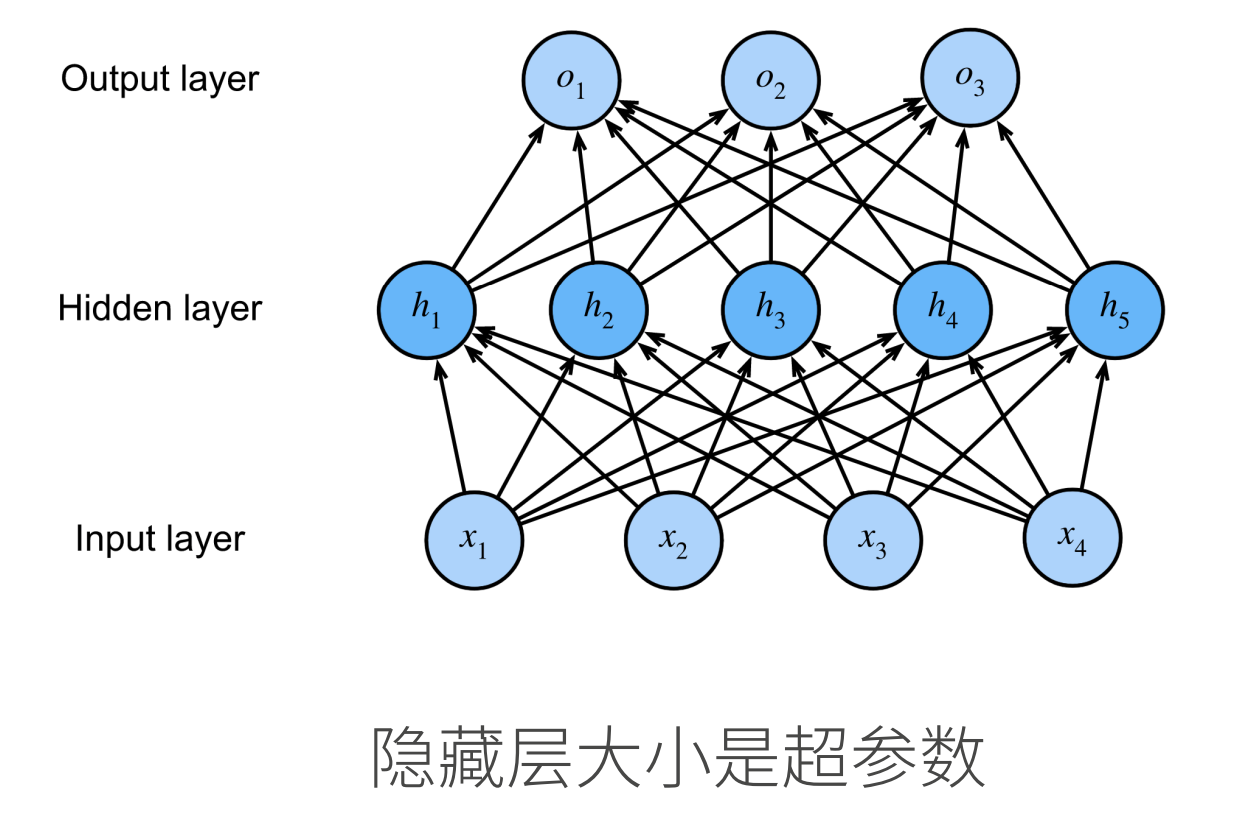
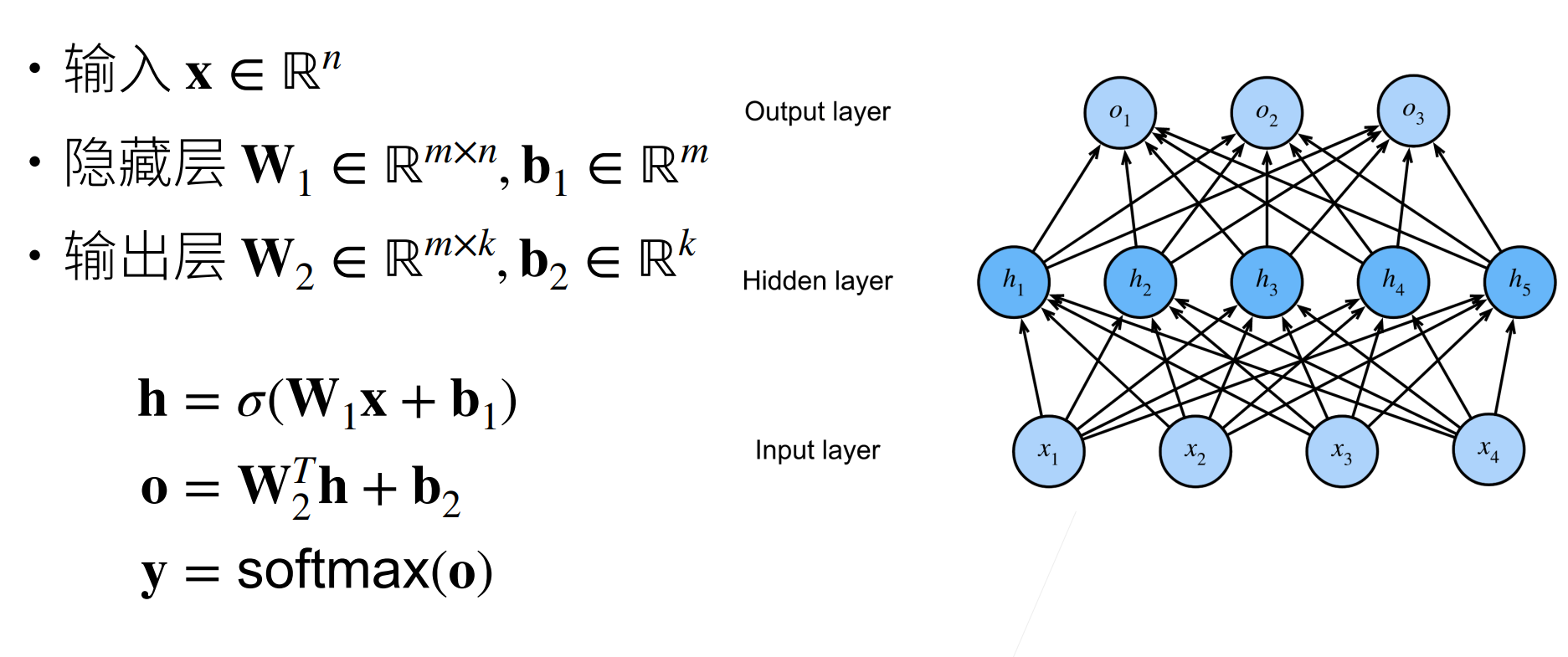
这个多层感知机有4个输入，3个输出，其隐藏层包含5个隐藏单元。输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。因此，这个多层感知机中的层数为2。注意，这两个层都是全连接的。每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

从线性到非线性（激活函数）

用数学向量表示就是，假设我们输入矩阵\(X\in R^{n*d}\),来表示n个样本的小批量，每个样本具有d个输入特征。对于具有h个隐藏单元的单隐藏层多层感知机，用\(H \in R^{n*h}\),由于输入层、隐藏层和输出层都是全连接的，所以我们又隐藏层的权重\(W^{(1)}\in R^{d*h}\)和隐藏层偏置\(b^{(1)}\in R^{1*h}\),已经输出层的权重\(W^{(2)}\in R^{h*q}\)和输出层偏置\(b^{(2)}\in R^{1*q}\)，输出为\(O\in R^{n*q}\):

\[H=XW^{(1)}+b^{(1)} \]

\[O=HW^{(2)}+b^{(2)} \]

注意在添加隐藏层之后，模型现在需要跟踪和更新额外的参数。模型依然是线性的，也就等价于我们之前的线性模型。 上面的隐藏单元由输入的仿射函数给出，而输出（softmax操作前）只是隐藏单元的仿射函数。仿射函数的仿射函数本身就是仿射函数，但是我们之前的线性模型已经能够表示任何仿射函数。
我们可以证明这⼀等价性，即对于任意权重值，我们只需合并隐藏层，便可产生具有参数\(W=W^{(1)}W^{(2)}\)和\(b= b^{(1)}W^{(2)}+b^{(2)}\)的等价单层模型：

\[O=(XW^{(1)}+b^{(1)})W^{(2)}+b^{(2)} \]

\[= XW^{(1)}W^{(2)}+b^{(1)}W^{(2)}+b^{(2)} \]

\[= XW'+b' \]

为了发挥多层架构的潜力，我们需要在每个隐藏单元应用非线性的激活函数\(\sigma\)。一般来说有了激活函数，就不可能再将我们的多层感知机退化成线性模型，注意如果你不加激活函数的话，很有可能退化成线性模型。加上之后:

\[H=\sigma(XW^{(1)}+b^{(1)}) \]

\[O=HW^{(2)}+b^{(2)} \]

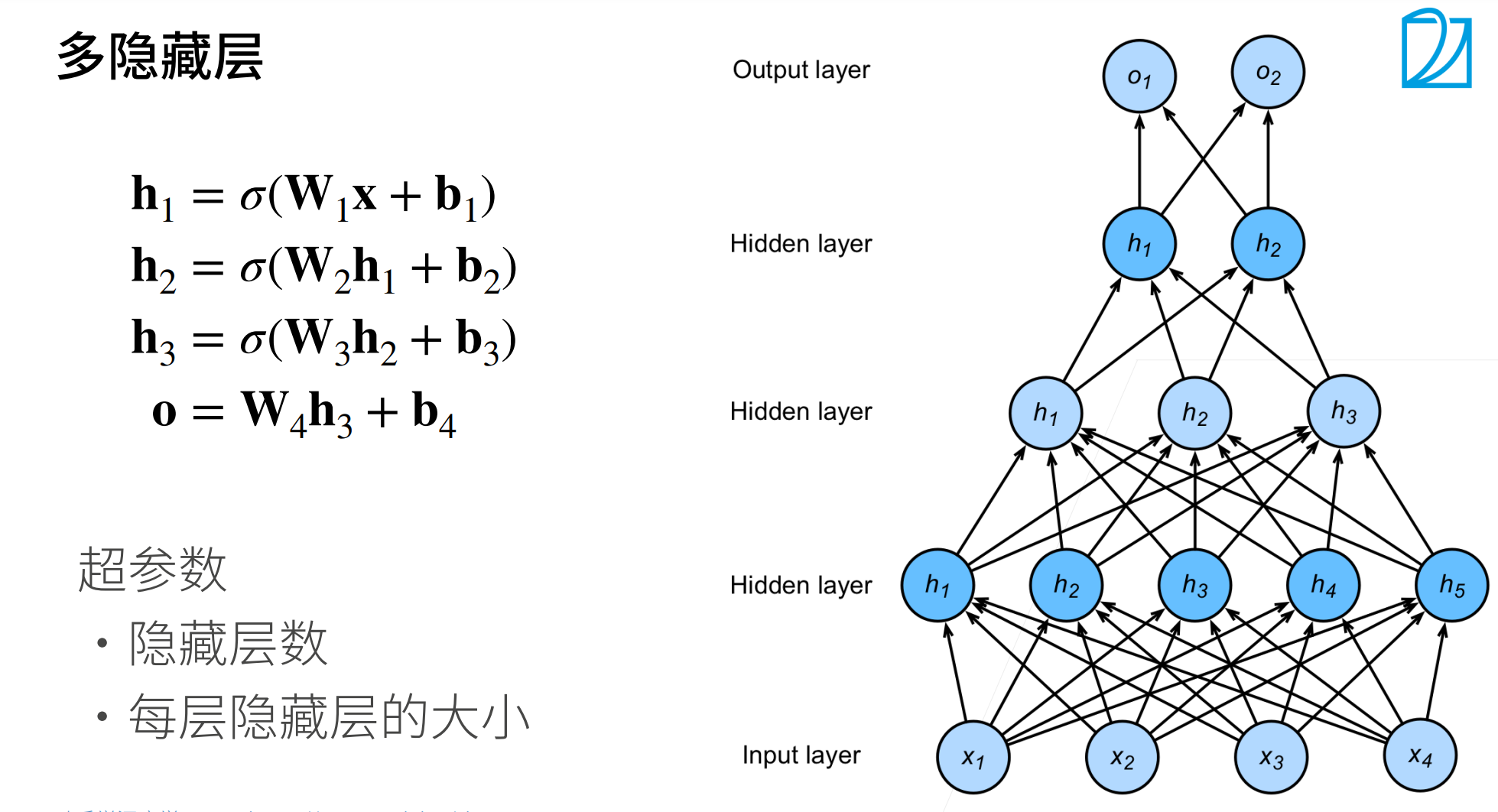
为了构建更通用的多层感知机，我们可以继续堆叠这样的隐藏层，例如\(H^{(1)}=\sigma_1(XW^{(1)}+b^{(1)})\)和\(H^{(2)}=\sigma_2(H^{(1)}W^{(2)}+b^{(2)})\)，⼀层叠⼀层，从而产生更有表达能力的模型。

激活函数

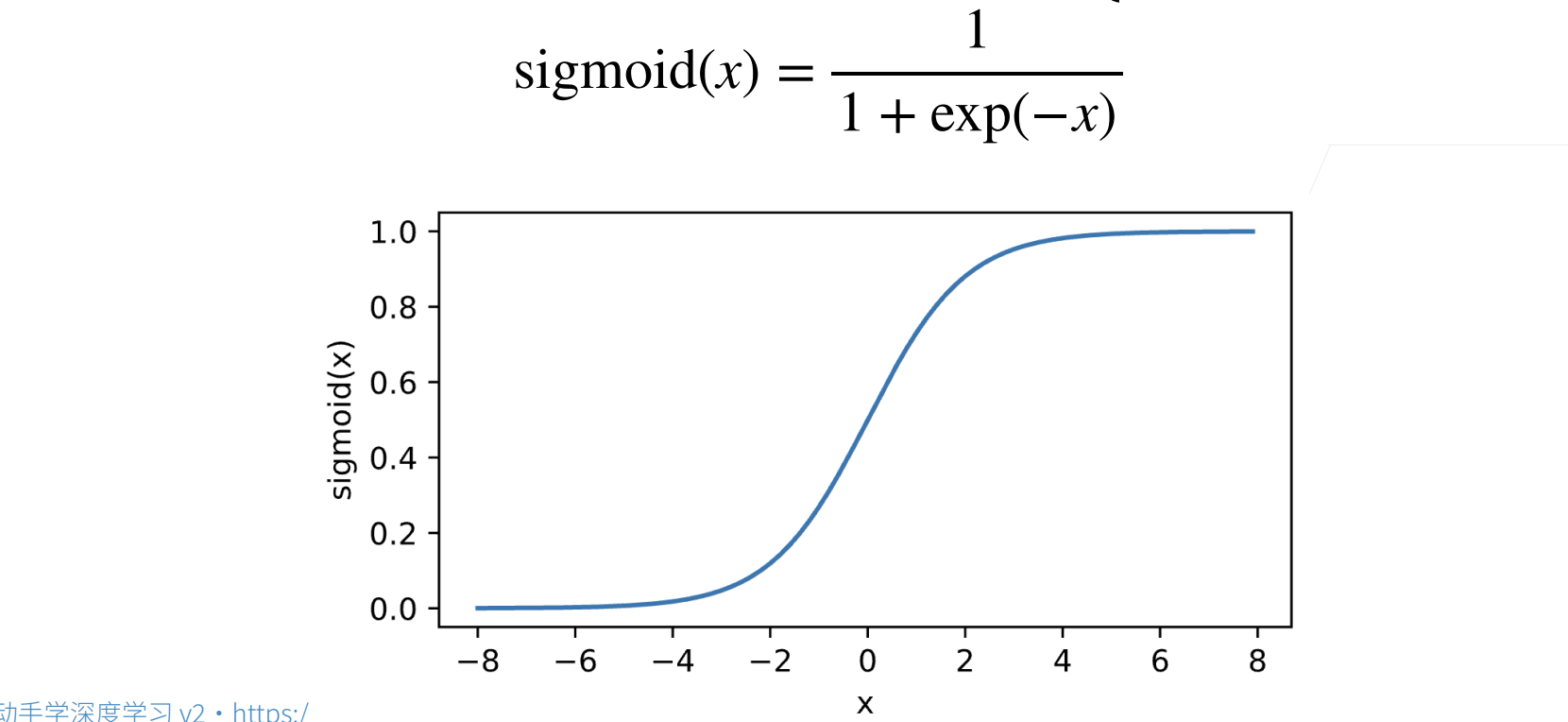
sigmoid激活函数

对于⼀个定义域在R中的输入，sigmoid函数将输入变换为区间(0, 1)上的输出。

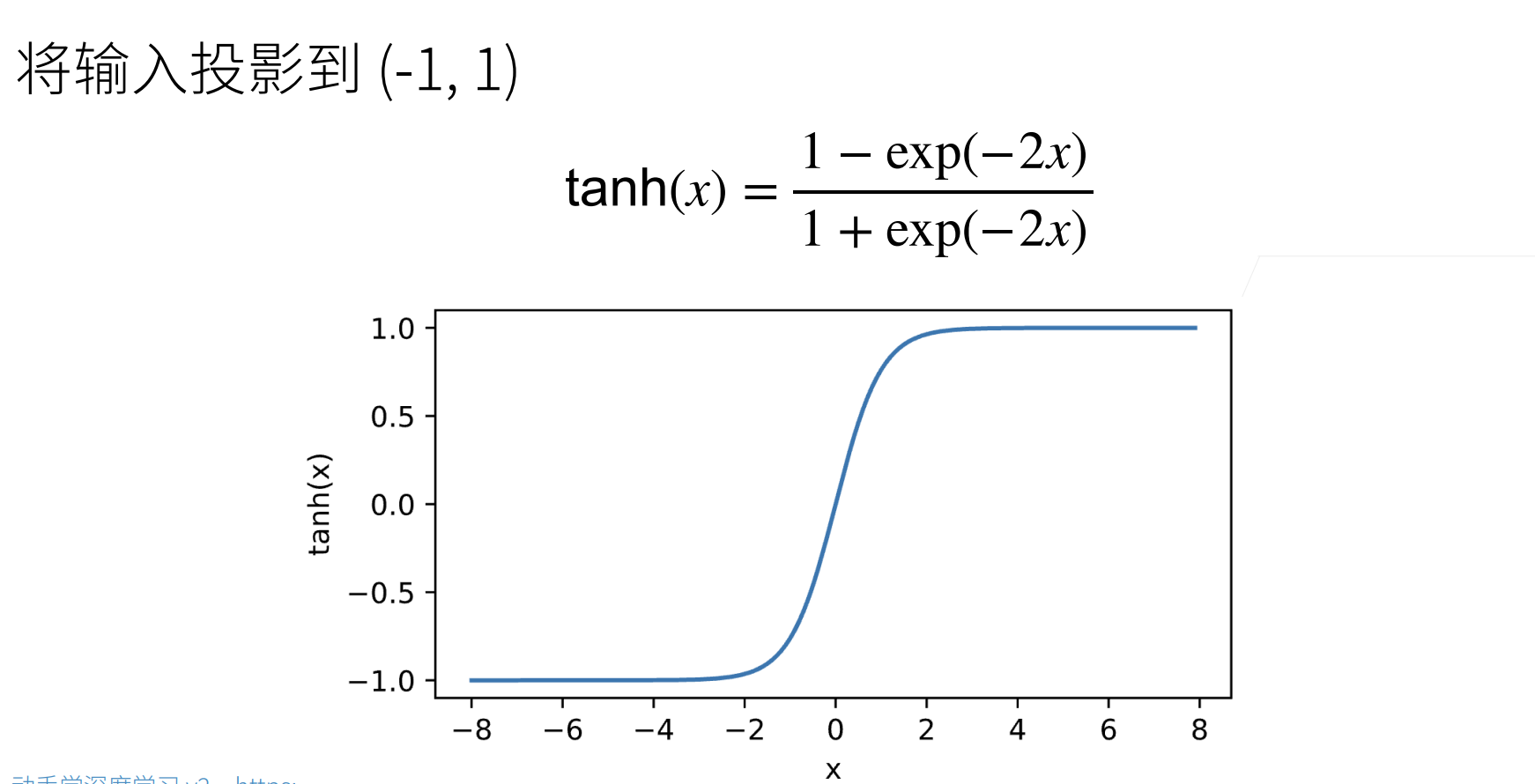
tanh函数

与sigmoid函数类似，tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上：

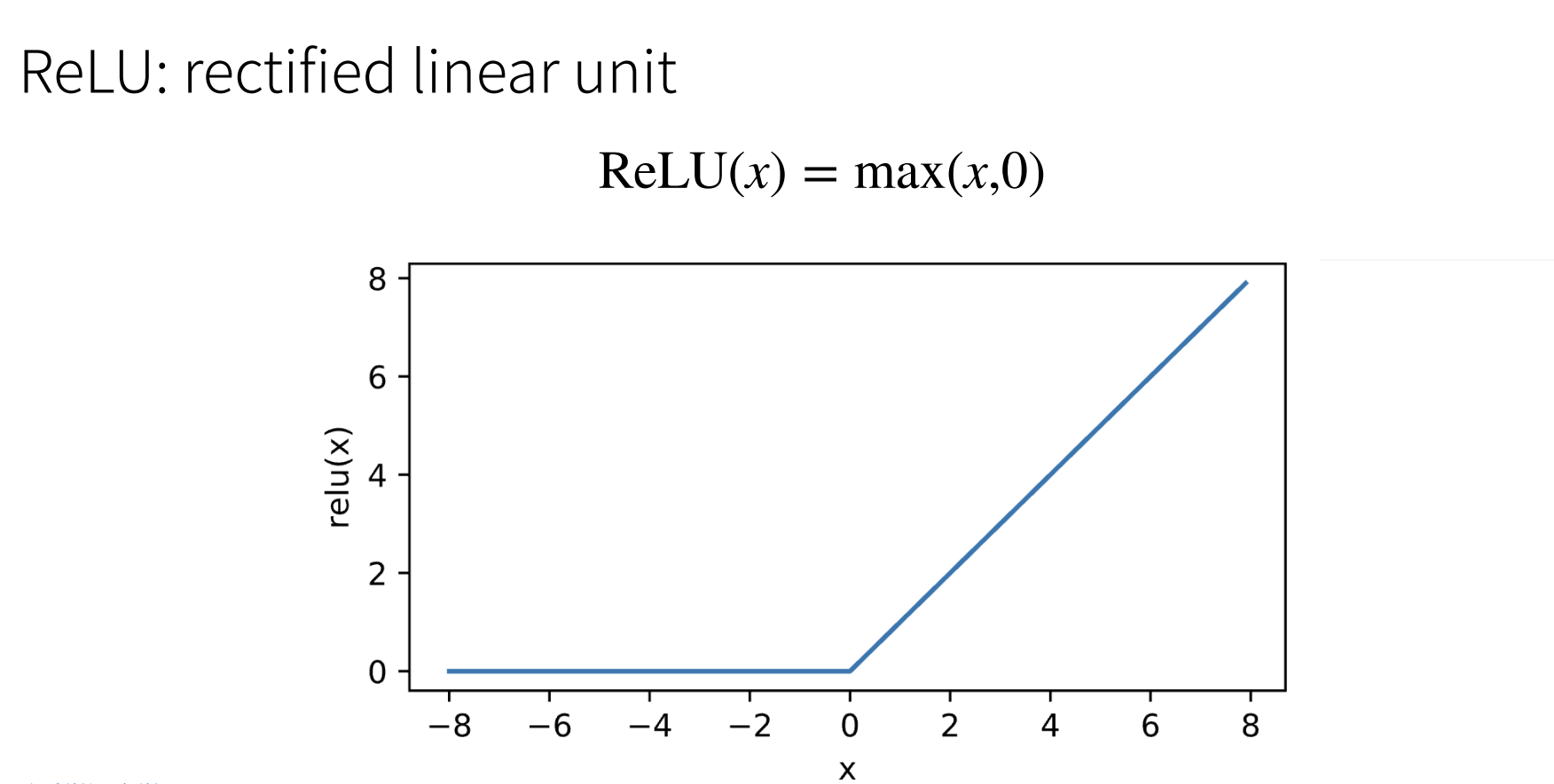
ReLU

最受欢迎的激活函数是ReLU,因为它实现简单，同时在各种预测任务中表现良好。

多类分类，多隐藏层

单隐藏层：

多隐藏层:

在实际的训练中我们设计每一个隐藏层的大小通常采取两个：

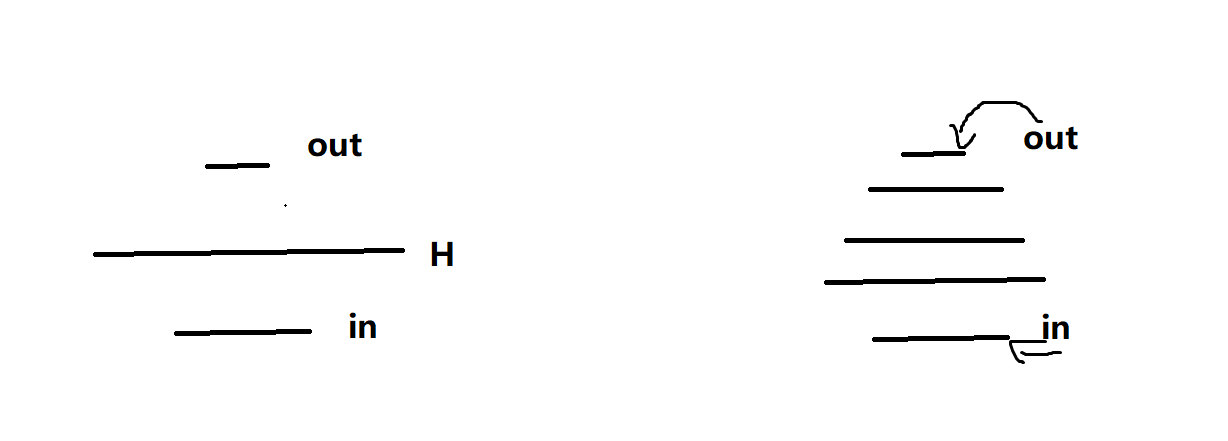
一是：我们可以设计一个隐藏层，然后让它很大，在一下缩小。
二是：我们可以设计第二个扩张一些，然后慢慢缩小，这样让它慢慢学，一次学习一些，也可以。
但是我们一般不会让它先变小在变大，这样在变小的时候会丢失很多东西。后面CNN的时候除外。
总结
·多层感知机使用隐藏层和激活函数来得到非线性模型
·常用激活函数是Sigmoid，Tanh，ReLU
·使用Softmax来处理多类分类
·超参数为隐藏层数，和各个隐藏层大小

多层感知机的从零开始实现

import torch
from torch import nn
from d2l import torch as d2l

• 加载数据

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

• 初始化模型参数

Fashion-MNIST中的每个图像由 28 × 28 = 784个灰度像素值组成。所有图像共分为10个类别。忽略像素之间的空间结构，我们可以将每个图像视为具有784个输⼊特征和10个类的简单分类数据集。我们将实现⼀个具有单隐藏层的多层感知机，它包含256个隐藏单元。通常，我们选择2的若干次幂作为层的宽度。因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。我们用几个张量来表示我们的参数。注意，对于每⼀层我们都要记录⼀个权重矩阵和⼀个偏置向量。跟以前⼀样，我们要为损失关于这些参数的梯度分配内存。

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(
    torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(
    torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

• 激活函数

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

• 模型

因为我们忽略了空间构造，所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。只需几行代码就可以实现我们的模型。

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X @ W1 + b1)
    return (H @ W2 + b2)

• 损失函数

还是交叉熵损失

loss = nn.CrossEntropyLoss()

• 训练

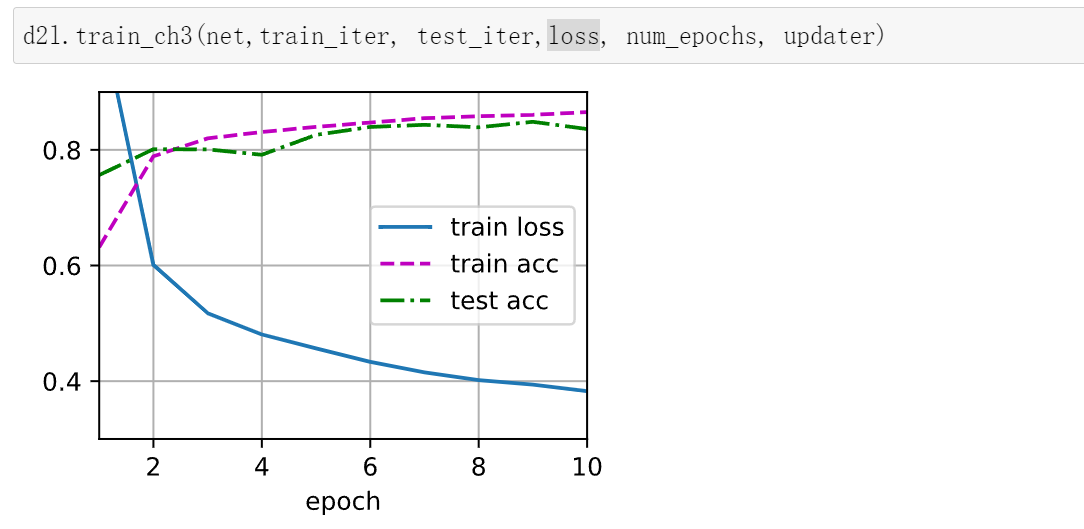
多层感知机的训练过程与softmax回归的训练过程完全相同。可以直接调⽤d2l包的train_ch3函数。

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

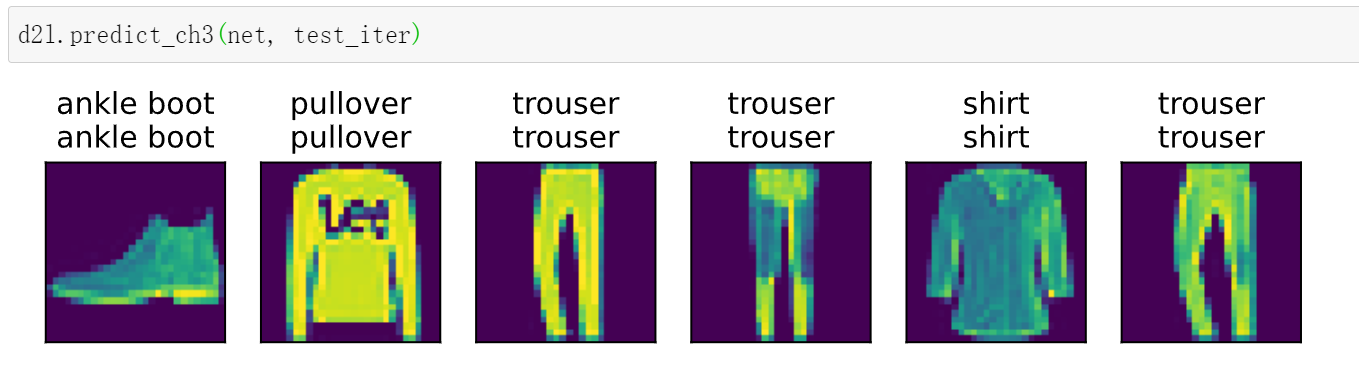
• 预测

d2l.predict_ch3(net, test_iter)

多层感知机的简洁实现

import torch
from torch import nn
from d2l import torch as d2l

• 模型

net = nn.Sequential(
    nn.Flatten(), 
    nn.Linear(784, 256), 
    nn.ReLU(),
    nn.Linear(256, 10)
)

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

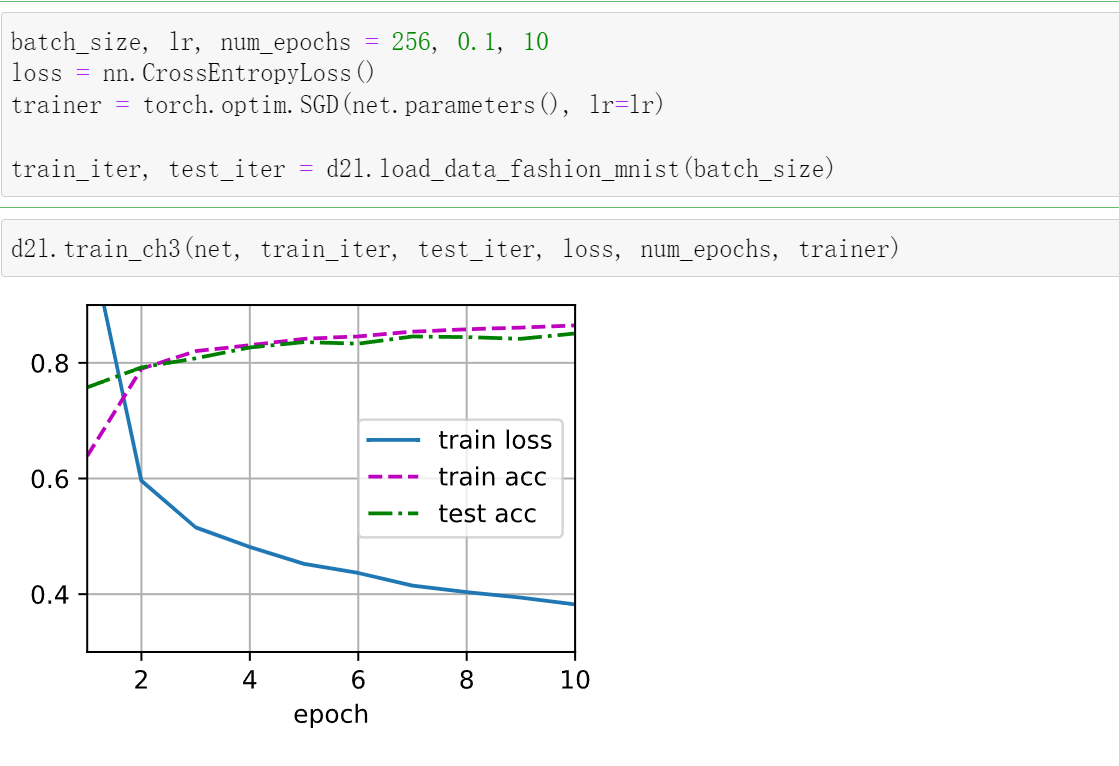
• 训练

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)