线段数维护区间乘，欧拉函数和

The Euler function, φ, is known to be important in math theory. Given a positive integer n, φ(n) is defined as the number of integers in [1,n] that are co-prime with n. For example, φ(1)=1,φ(10)=4,φ(11)=10.

Now, given an array x with n positive integers x1​,…,xn​, your task is to maintain m operations on x, which can be categorized into two types:

 

 

 

 

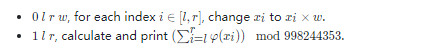
Input

The first line contains two inetegers n,m (1≤n,m≤105).

The second line contains n integers x1​,…,xn​ (1≤xi​≤100).

Then m lines follow. The i-th line describes the i-th operation. The input guarantees that 1≤l≤r≤n and 1≤w≤100.

Output

For each operation of type 1, output a single line with a single integer, representing the answer.

Sample Input

5 5
1 2 3 4 5
1 1 5
0 1 3 2
1 1 5
0 2 5 6
1 1 5

 

结尾无空行

Sample Output

10
11
37


这个题就是首先你要先知道欧拉函数的性质，ol[i]=n*(1-1/p1)*(1-1/p2)*(1-1/p3).......*(1-1/pn)
这个题就是用到这个性质，然后这a[i]和乘的每一个数都是<=100的质因子也就25个，可以用一个bitset来维护一下，

#include<iostream>
#include<algorithm>
#include<bitset>
using namespace std;
typedef long long ll;
const int maxn=5e5+100;
const ll mod = 998244353;
bitset<30>st[105];
struct node{
    bitset<30> st;
    ll x,lazy;
    int l,r;
}t[maxn];
int n,m;
int vis[maxn];
int idx;
int a[maxn],pri[100],cnt[105][30];
int f[maxn];//欧拉函数 
void inint(){
    for(int i=2;i<=100;i++){
        if(!vis[i]){
            pri[++idx]=i;
        }
        for(int j=1;j*pri[i]<maxn&&j<=idx;j++){
            vis[i*pri[j]]=1;
            if(i%pri[j]==0){
                break;
            }
        }
    }
    for(int i=1;i<=100;i++){
        for(int j=1;j<=25;j++){
            int tmp=i;
            while(tmp%pri[j]==0){
                ++cnt[i][j];
                tmp/=pri[j];
            }
            st[i][j]=cnt[i][j];
        }
    }
}
int ol(int n){
    int ans=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            ans=ans/i*(i-1);
            while(n%i==0){
                n/=i;
            }
        }
    }
    if(n>1){
        ans=ans/n*(n-1);
    }
    return ans;
}
void push_up(int p){
    t[p].x=(t[2*p].x+t[2*p+1].x)%mod;
    t[p].st=(t[2*p].st & t[2*p+1].st);
}
void push_down(int p){
    t[2*p].lazy=(t[2*p].lazy*t[p].lazy)%mod;
    t[2*p+1].lazy=(t[2*p+1].lazy*t[p].lazy)%mod;
    t[2*p].x=(t[2*p].x*t[p].lazy)%mod;
    t[2*p+1].x=(t[2*p+1].x*t[p].lazy)%mod;
    t[p].lazy=1;     
}
void build(int p,int l,int r){
    t[p].l=l;
    t[p].r=r;
    t[p].lazy=1;
    if(t[p].l==t[p].r){
        t[p].x=1ll*f[a[l]];
        t[p].lazy=1;
        t[p].st=st[a[l]];
        return ;
    }
    int mid=(l+r)/2;
    build(2*p,l,mid);
    build(2*p+1,mid+1,r);
    push_up(p);
}
void update(int p,int l,int r,int x,int y){
    if(t[p].l>=l&&t[p].r<=r&&t[p].st[x]){
        for(int i=1;i<=y;i++){
            t[p].x=(t[p].x*pri[x])%mod;
            t[p].lazy=(t[p].lazy*pri[x])%mod;
        }
        return ;
    }
    if(t[p].l==t[p].r){
        t[p].x=(t[p].x*(pri[x]-1))%mod;
        t[p].st[x]=1;
        for(int i=1;i<=y-1;i++){
            t[p].x=(t[p].x*pri[x])%mod;
        }
        return ;
    }
    if(t[p].lazy!=1){
        push_down(p);
    }
    int mid=(t[p].l+t[p].r)/2;
    if(l<=mid){
        update(2*p,l,r,x,y);
    }
    if(r>mid){
        update(2*p+1,l,r,x,y);
    }
    push_up(p);
} 
ll query(int p,int l,int r){
    if(t[p].l>=l&&t[p].r<=r){
        return t[p].x;
    }
    ll ans=0;
    if(t[p].lazy!=1){
        push_down(p);
    }
    int mid=(t[p].l+t[p].r)/2;
    if(l<=mid){
        ans+=query(2*p,l,r);
    }
    if(r>mid){
        ans+=query(2*p+1,l,r);
    }
    return ans;
}
//ll query(int p, int a, int b)
//{
//    if(a <= t[p].l && t[p].r <= b) return t[p].x;
//
//    if(t[p].lazy != 1) push_down(p);
//    int mid = (t[p].l + t[p].r) >> 1;
//    if(mid >= b) return query(p<<1, a, b);
//    else if(mid < a) return query(p<<1|1, a, b);
//    else return (query(p<<1, a, b) + query(p<<1|1, a, b)) % mod;
//}
int main(){
    inint();
    f[1]=1;
    for(int i=2;i<=100;i++){
        f[i]=ol(i);
    }
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    } 
    build(1,1,n);
    int op,a,b,c;
    while(m--){
        scanf("%d",&op);
        if(op==1){
            scanf("%d%d",&a,&b);
            printf("%lld\n",query(1,a,b)%mod);
        }
        else{
            scanf("%d%d%d",&a,&b,&c);
            for(int i=1;i<=25;i++){
                if(cnt[c][i]){
                    update(1,a,b,i,cnt[c][i]);
                }
            }
        }
    } 
}