GCD of an Array（multiset或者线段树+数论）

题目

题目链接

You are given an array aa of length nn. You are asked to process qq queries of the following format: given integers i and x, multiply ai by x.

After processing each query you need to output the greatest common divisor (GCD) of all elements of the array a.

Since the answer can be too large, you are asked to output it modulo 10^9+7.

Input

The first line contains two integers — n and q (1≤n,q≤2⋅10^5).

The second line contains nn integers a1,a2,…,an (1≤ai≤2⋅10^5) — the elements of the array aa before the changes.

The next q lines contain queries in the following format: each line contains two integers i and x (1≤i≤n, 1≤x≤2⋅10^5).

Output

Print q lines: after processing each query output the GCD of all elements modulo 10^9+7 on a separate line.

4 3
1 6 8 12
1 12
2 3
3 3

output

Copy

2
2
6

Note

After the first query the array is [12,6,8,12], gcd(12,6,8,12)=2.

After the second query — [12,18,8,12], gcd(12,18,8,12)=2.

After the third query — [12,18,24,12], gcd(12,18,24,12)=6.

Here the gcdgcd function denotes the greatest common divisor.

 

 

于是很容易想到维护数组每个数质因数分解后的幂次，而pk对最终gcd的贡献是,就是每一个质因子的最小值。

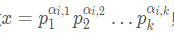而对某个位置i×一个数这些值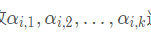（准确来说是＋上一个数，我们只需要记录之前的值，把之前的贡献减去，

然后把现在的贡献加上即可）

而对于贡献的维护我们需要一个能够支持插入，删除，最小值的数据结构，这里使用multiset
trick：对于初始数组可以看出一个操作i ,ai 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<set>
#include<map> 
using namespace std;
typedef long long ll;
const int maxn=1e6+100;
const int mod=1e9+7;
ll a[maxn];
multiset<int>s[maxn];
map<int,int>mp[maxn];
ll n,q;
ll d;
ll qpow(ll a,ll b,ll mod){
    ll ans=1;
    while(b){
        if(b&1){
            ans=(ans*a)%mod;
        }
        a=(a*a)%mod;
        b/=2;
    }    
    return ans;
}
void insert(int k,int i,int cnt){
    if(mp[k].count(i)){//如果有这个数 
        if(s[i].size()==n){
            d=d*qpow(qpow(i,*s[i].begin(),mod),mod-2,mod)%mod;//如果这个数原本就出现了n次，先清除答案中质因子a在ai中的贡献
        }
        s[i].erase(s[i].find(mp[k][i]));
        mp[k][i]=mp[k][i]+cnt;
        s[i].insert(mp[k][i]);
        if(s[i].size()==n){
            d=d*qpow(i,*s[i].begin(),mod)%mod;
        }
    }
    else{
        mp[k][i]=cnt;
        s[i].insert(mp[k][i]);
        if(s[i].size()==n) d=d*qpow(i,*s[i].begin(),mod)%mod;
    } 
}
void divide(int k,int x){
    for(int i=2;i*i<=x;i++){
        if(x%i==0){
            int cnt=0;
            while(x%i==0){
                x/=i;
                cnt++;
            }
            insert(k,i,cnt);
        }
    }
    if(x>1){
        insert(k,x,1);
    }
}
int main(){
    cin>>n>>q;
    for(int i=1;i<=n;i++){
        cin>>a[i]; 
    } 
    d=1;
    for(int i=1;i<=n;i++){
        divide(i,a[i]);
    }
    while(q--){
        int i,x;
        cin>>i>>x;
        divide(i,x);
        cout<<d<<"\n";
    }
    return 0;
}

这个题也可以用线段树，就是给每一个质因子开一个线段数。暂时还没看懂

传送门