E. Boring Segments(线段树覆盖问题）

You are given

You are asked to select a subset of these segments (possibly, all of them). Once the subset is selected, it's possible to travel between two integer points if there exists a selected segment that covers both of them. A subset is good if it's possible to reach point

The cost of the subset is the difference between the maximum and the minimum values of segments in it. Find the minimum cost of a good subset.

In every test there exists at least one good subset.

Input

The first line contains two integers

Each of the next

In every test there exists at least one good subset.

Output

Print a single integer — the minimum cost of a good subset.

Examples

input

Copy

output

Copy

input

Copy

1 10
1 10 23

output

Copy

题目大意

这个题的题目意思就是给你一些线段，每一个线段都有一个权值，让选出一些线段，能够覆盖[1,m]，并且这些线段（最大权值-最小权值）的最小值

题解

将线段按照w从小到大排序.

然后从左到右枚举线段r,
尺取维护一个最大的l,满足[l,r]能够覆盖[1,m],
判断[l,r]中的线段能否覆盖[1,m],可以用线段树区间加法,
维护每个点被覆盖的次数,同时维护区间最小值,
如果最小值>0,说明全覆盖了.

对于满足条件的区间,用w的差值更新答案即可.

算法总复杂度O(n*log)

ps:
这题其实说的不是区间覆盖,而是能够连通,
例如[1,3]和[4,5]是不连通的,因为线段之间没有相交
而[1,3]和[3,5]是连通的.
处理方法是将m--,每条线段的右端点r--,
这样的话就不需要判相交,只需要判断是否覆盖了[1,m]就行了.

代码

#include<iostream>
#include<algorithm>
const int maxn=5e6+100;
using namespace std;
struct node{
    int l,r,mi;//与其说是最小值，还不如说是和，就是取有一个最小值 
    int lazy;
}t[maxn];
struct Node{
    int l,r,w;
    bool friend operator<(Node a,Node b){
        return a.w<b.w; 
    }
}save[maxn];
void pushdown(int p){
    if(t[p].lazy){
        t[2*p].lazy+=t[p].lazy;
        t[2*p+1].lazy+=t[p].lazy;
        t[2*p].mi+=t[p].lazy;
        t[2*p+1].mi+=t[p].lazy;
        t[p].lazy=0;
    }
}
void pushup(int p){
    t[p].mi=min(t[2*p].mi,t[2*p+1].mi);
} 
void build(int p,int l,int r){
    t[p].l=l;
    t[p].r=r;
    t[p].mi=t[p].lazy=0;
    if(l==r){
        return ;
    }
    int mid=(l+r)/2;
    build(2*p,l,mid);
    build(2*p+1,mid+1,r);
    pushup(p);
}
void update(int p,int l,int r,int val){
    if(t[p].l>=l&&t[p].r<=r){
        t[p].mi+=val;
        t[p].lazy+=val;
        return ; 
    }
    int mid=(t[p].l+t[p].r)/2;
    pushdown(p);
    if(l<=mid){
        update(2*p,l,r,val);
    } 
    if(r>mid){
        update(2*p+1,l,r,val);
    }
    pushup(p); 
} 
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d%d%d",&save[i].l,&save[i].r,&save[i].w);
        save[i].r--; 
    }
    sort(save+1,save+1+n);
    build(1,1,m-1);
    int ans=0x3f3f3f3f;
    for(int R=1,L=1;R<=n;R++){
        update(1,save[R].l,save[R].r,1);
        while(t[1].mi){//这里的t[1].mi就是区间1-m的最小值
            ans=min(ans,save[R].w-save[L].w);
            update(1,save[L].l,save[L].r,-1);
            L++;
        }
    }
    cout<<ans<<endl;
}

题目二：

传送门

在数轴上有 n 个闭区间从 1 至 n 编号，第 i 个闭区间为 [li,ri] 。

现在要从中选出 m 个区间，使得这 m 个区间共同包含至少一个位置。换句话说，就是使得存在一个 x ，使得对于每一个被选中的区间[li,ri]，都有li≤x≤ri 。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。

区间[li,ri] 的长度定义为 (ri−li) ，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 −1。

输入格式

第一行包含两个整数，分别代表 n 和 m。

第 2 到第 (n+1) 行，每行两个整数表示一个区间，第(i+1) 行的整数 i,ri 分别代表第 i 个区间的左右端点。

输出格式

输出一行一个整数表示答案。

输入输出样例

输入

输出

说明/提示

样例输入输出 1 解释

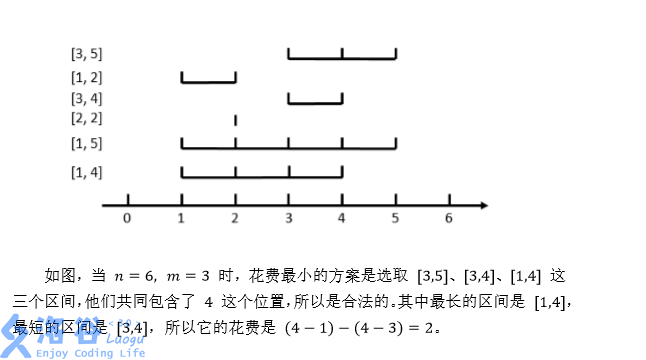
对于全部的测试点，保证 $1≤n≤5×10^5，1≤m≤2×10^5，0≤li≤ri≤10^9。$

解题思路：

这个题其实和上面的那个题是一样的，就是这个题的li和ri都很大，需要离散化，然后按照长度排个序，然后再用尺取，

这个为啥能用出去呢？因为你是按照长度排好序的，就是如果[L,R]是满足条件的，然后R向右移动，然后是可以保证这个L也是向右

移动的，向左移动只会答案增加。然后还有一个问题就是判断怎么样判断是否满足条件呢，这个是可以用线段树来维护的，

这个每次可以在[li,ri]区间+1，然后判断[1,cnt]的最大值是不是>=m，这个max[1,cnt]就是t[1].ma

代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
const int maxn=4e6+100;
int n,m;
struct node{
    int l,r;
    int ma,lazy;
}t[maxn];
struct Node{
    int l,r,w;
    bool friend operator<(Node x,Node y){
        return x.w<y.w;
    }
}save[maxn];
int id[maxn];
int cnt=0;
int getid(int x){
    return lower_bound(id+1,id+cnt+1,x)-id;
}
void pushup(int p){
    t[p].ma=max(t[2*p].ma,t[2*p+1].ma);
}
void build(int p,int l,int r){
    t[p].l=l;
    t[p].r=r;
    t[p].lazy=0,t[p].ma=0;
    if(l==r){
        return ;
    }
    int mid=(l+r)/2;
    build(2*p,l,mid);
    build(2*p+1,mid+1,r);
    pushup(p);
} 
void pushdown(int p){
    if(t[p].lazy){
        t[2*p].ma+=t[p].lazy;
        t[2*p+1].ma+=t[p].lazy;
        t[2*p].lazy+=t[p].lazy;
        t[2*p+1].lazy+=t[p].lazy; 
        t[p].lazy=0;
    }
}
void update(int p,int l,int r,int val){
    if(t[p].l>=l&&t[p].r<=r){
        t[p].ma+=val;
        t[p].lazy+=val;
        return ;
    }
    int mid=(t[p].l+t[p].r)/2;
    pushdown(p);
    if(l<=mid){
        update(2*p,l,r,val);
    }
    if(r>mid){
        update(2*p+1,l,r,val);
    }
    pushup(p);
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d%d",&save[i].l,&save[i].r);
        id[++cnt]=save[i].l,id[++cnt]=save[i].r;
        save[i].w=(save[i].r-save[i].l);
    }
    sort(save+1,save+1+n);
    sort(id+1,id+cnt+1);
    cnt=unique(id+1,id+1+cnt)-(id+1); 
    for(int i=1;i<=n;i++){
        save[i].l=getid(save[i].l);
        save[i].r=getid(save[i].r); 
    } 
    build(1,1,cnt);
    int ans=0x3f3f3f3f;
    for(int R=1,L=1;R<=n;R++){
        update(1,save[R].l,save[R].r,1);
        while(t[1].ma>=m){ 
            ans=min(ans,save[R].w-save[L].w);
            //cout<<ans<<endl;
            update(1,save[L].l,save[L].r,-1);    
            L++; 
        }
    }
    if(ans==0x3f3f3f3f){
        cout<<-1<<endl;
    }
    else{
        cout<<ans<<endl;
    }
}

posted @ 2021-08-02 17:31 lipu123 阅读(169) 评论(0) 收藏举报

刷新页面返回顶部

lipu123

E. Boring Segments(线段树覆盖问题）

题目一:

题目大意

题解

代码

题目二：

输入格式

输出格式

输入输出样例

说明/提示

样例输入输出 1 解释

解题思路：

代码

公告