Count Descendants（过定点树上一定距离的点个数）

题目链接

我们有一棵有根的树，有 N 个顶点，编号为 1,2,...,N。
顶点 1 是根，顶点 i(2≤i≤N) 的父节点是顶点 Pi。
您将收到 Q 查询。在第 i 个查询 (1≤i≤Q) 中，给定整数 Ui 和 Di，找到满足以下所有条件的顶点 u 的数量：

顶点 Ui 在从 u 到根（包括端点）的最短路径中）。
在从 u 到根的最短路径中正好有 Di 边。
约束条件
2≤N≤2×10^5
1≤Pi<i
1≤Q≤2×10^5
1≤Ui≤N
0≤Di≤N−1
input 中的所有值都是整数。

题意：这个题就是给你一颗树，

然后给你m次查询，每一次查询给你两个整数，Ui 和 Di,然后问你经过Ui这个点的，并且到顶点的距离为Di的顶点的数量为多少。

这题技巧性好强,我们从根节点遍历整颗树,用时间轴记录搜到和离开的时间in[i]和out[i],同时存入同一深度的所有in[i],方便后面计算.对于某个父亲结点u,它的一个子树结点为v,必然满足:in[u]≤in[v]<out[u].那么对于每次询问的Ui,我要去找深度为d的它或它的子树结点,也就是找出所有深度为d且满足in[u]≤in[v]<out[u]的点,这里可以用二分查找.

 

 

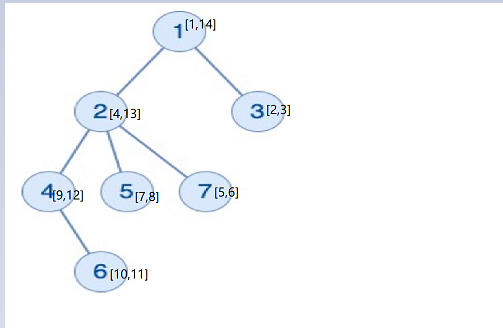
做完dfs序之后每一个节点都有一个唯一的标记：

深度为1的点为：1

深度为2的点为：2 4

深度为3的点为：5 7 9

深度为4的点为：10

这样求过1这个点的深度为3的点就是找5 7 9 在【1，14】中的个数，就是3

 

#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
#define rep(a,b,c) for(int a=b;a<=c;++a)
#define per(a,b,c) for(int a=b;a>=c;--a)
const int N = 1e6 + 10;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}

int n;
int p;
vector<int> edge[N];
int q;
int u,d;
vector<int> v[N];
int timestamp;
int in[N],out[N];

void dfs(int u,int dep){
    in[u]=timestamp++;
    v[dep].pb(in[u]);
    for(auto w:edge[u]){
        dfs(w,dep+1);    
    }    
    out[u]=timestamp++;
}

int main() {
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    cin>>n;
    for(int i=2;i<=n;++i){
        cin>>p;
        edge[p].pb(i);
    }

    dfs(1,0);

    cin>>q;
    for(int i=1;i<=q;++i){
        cin>>u>>d;
        cout<<lower_bound(v[d].begin(),v[d].end(),out[u])-lower_bound(v[d].begin(),v[d].end(),in[u])<<'\n';
    }


    return 0;
}

 

#include<bits/stdc++.h>
using namespace std;
 
vector<int> ve[200005];
bool vis[200005];
int in[200005];
int out[200005];
vector<int> ce[200005];
int tim=0;
int ceng;
 
void dfs(int x,int step)
{
    ceng=max(ceng,step);
    vis[x]=1;
    in[x]=++tim;
    ce[step].push_back(in[x]);
    int Size=ve[x].size();
    for(int i=0;i<Size;i++)
    {
        if(!vis[ve[x][i]])
        {
            dfs(ve[x][i],step+1);
        }
    }
    out[x]=++tim;
}
 
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=2;i<=n;i++)
    {
        int temp;
        scanf("%d",&temp);
        ve[temp].push_back(i);
        ve[i].push_back(temp);
    }
    dfs(1,1);
    int q;
    scanf("%d",&q);
    while(q--)
    {
        int u,d;
        scanf("%d%d",&u,&d);
        d++;
        int l=lower_bound(ce[d].begin(),ce[d].end(),in[u])-ce[d].begin();
        int r=upper_bound(ce[d].begin(),ce[d].end(),out[u])-ce[d].begin();
        printf("%d\n",r-l);
    }
    return 0;
}