1937. 扣分后的最大得分（dp优化：拆项+前后缀最大值）

1937. 扣分后的最大得分

 

给你一个 m x n 的整数矩阵 points （下标从 0 开始）。一开始你的得分为 0 ，你想最大化从矩阵中得到的分数。

你的得分方式为：每一行 中选取一个格子，选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。

然而，相邻行之间被选中的格子如果隔得太远，你会失去一些得分。对于相邻行 r 和 r + 1 （其中 0 <= r < m - 1），选中坐标为 (r, c1) 和 (r + 1, c2) 的格子，你的总得分 减少 abs(c1 - c2) 。

请你返回你能得到的 最大 得分。

abs(x) 定义为：

• 如果 x >= 0 ，那么值为 x 。
• 如果 x < 0 ，那么值为 -x 。

 

示例 1：

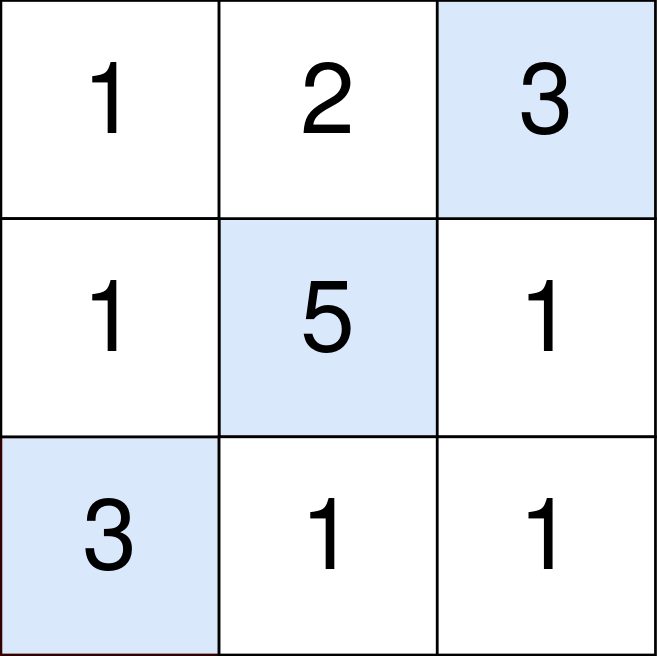
输入：points = [[1,2,3],[1,5,1],[3,1,1]]
输出：9
解释：
蓝色格子是最优方案选中的格子，坐标分别为 (0, 2)，(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。

示例 2：

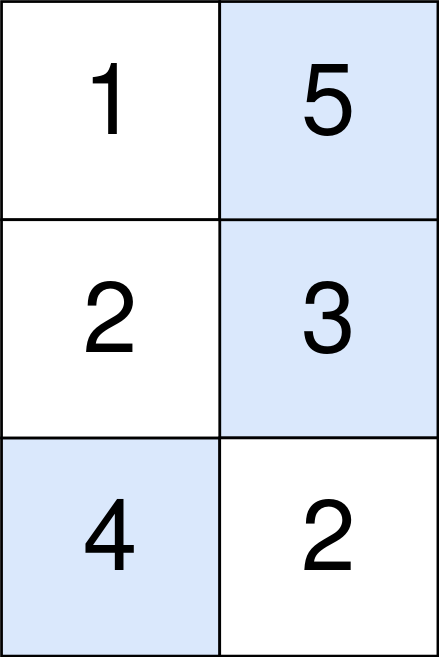
输入：points = [[1,5],[2,3],[4,2]]
输出：11
解释：
蓝色格子是最优方案选中的格子，坐标分别为 (0, 1)，(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。

 

提示：

• m == points.length
• n == points[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= points[r][c] <= 105

 首先看看官方题解把：传送门

 首先这个题肯定是个dp先写一个然后再优化把：

for(int i=0;i<n;i++){
    for(int j=0;j<m;j++){
        for(int k=0;k<m;k++){
            dp[i][j]=max(dp[i][j],dp[i][k]+p[i][j]);
        } 
    }
}
int ans=0;
for(int i=0;i<m;i++){
    ans=max(ans,dp[n-1][i]);
}

显然这个肯定会超时的，所以要优化：

首先我们从状态方程分析：

状态转移方程：

 

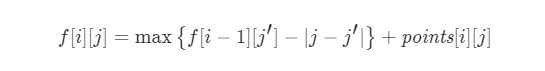
 最终的答案即为 f[m−1][0..n−1] 中的最大值。

优化的重点在于状态转移方程中的 | j - j' | 这一项

 

 

 

 

 就是这样：

 

就是加入说我们正向遍历的时候：f[i][j]=max(f[i][j],f[i][k]+k)+p[i][j]+j，这个k<=j的所以我们可以一边遍历一边求出f[i][k]+k的最大值

反向的时候也是这样

class Solution {
public:
    long long maxPoints(vector<vector<int>>& points) {
        int m=points.size();
        int n=points[0].size();
        vector<long long>v(n);
        for(int i=0;i<m;i++){
            vector<long long>g(n);
            long long lmax=LLONG_MIN;
            for(int j=0;j<n;j++){
                lmax=max(lmax,v[j]+j);
                g[j]=max(g[j],lmax+points[i][j]-j);
            }
            long long rmax=LLONG_MIN;
            for(int j=n-1;j>=0;j--){
                rmax=max(rmax,v[j]-j);
                g[j]=max(g[j],rmax+points[i][j]+j);
            }
            v=move(g);
        }
        return *max_element(v.begin(), v.end());
    }
};