多源最短路和BFS

这个是一个模型，就是有建立一个超级源点，然后转化为最短路问题

 

 就像上面的图一样就是，就是求右边的一个点到中间的5个点的最短距离，就是选择一个超级源点s,然后连接中间5个点和s他们的权值为0,然后跑一个最短路就解决了，

 

类似例题1：

视频连接

题目连接

 

栋栋最近开了一家餐饮连锁店，提供外卖服务。

随着连锁店越来越多，怎么合理的给客户送餐成为了一个急需解决的问题。

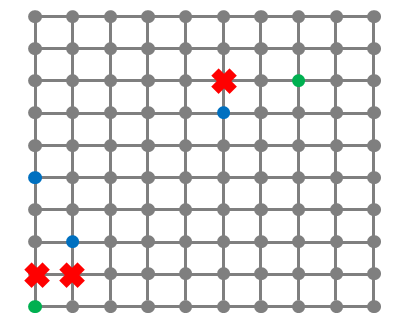
栋栋的连锁店所在的区域可以看成是一个 n×n 的方格图（如下图所示），方格的格点上的位置上可能包含栋栋的分店（绿色标注）或者客户（蓝色标注），有一些格点是不能经过的（红色标注）。

方格图中的线表示可以行走的道路，相邻两个格点的距离为 1。

栋栋要送餐必须走可以行走的道路，而且不能经过红色标注的点。

 

送餐的主要成本体现在路上所花的时间，每一份餐每走一个单位的距离需要花费 1 块钱。

每个客户的需求都可以由栋栋的任意分店配送，每个分店没有配送总量的限制。

现在你得到了栋栋的客户的需求，请问在最优的送餐方式下，送这些餐需要花费多大的成本。

输入格式

输入的第一行包含四个整数n,m,k,d，分别表示方格图的大小、栋栋的分店数量、客户的数量，以及不能经过的点的数量。

接下来 m 行，每行两个整数 xi,yi，表示栋栋的一个分店在方格图中的横坐标和纵坐标。

接下来 k 行，每行三个整数 xi,yi,ci，分别表示每个客户在方格图中的横坐标、纵坐标和订餐的量。（注意，可能有多个客户在方格图中的同一个位置）

接下来 d 行，每行两个整数，分别表示每个不能经过的点的横坐标和纵坐标。

输出格式

输出一个整数，表示最优送餐方式下所需要花费的成本。

数据范围

前 30% 的评测用例满足：1≤n≤20。
前 60% 的评测用例满足：1≤n≤100。
所有评测用例都满足：1≤n≤1000,1≤m,k,d≤n2,1≤xi,yi≤n。
可能有多个客户在同一个格点上。
每个客户的订餐量不超过 1000，每个客户所需要的餐都能被送到。

 

输入样例：

10 2 3 3
1 1
8 8
1 5 1
2 3 3
6 7 2
1 2
2 2
6 8

输出样例：

29
然后这个题和上面的模型差不多，就是这个距离是1，所以可以用BFS，如果不是1的话，就要用dijkstra算法了，
这个题其实不用建立超级源点的，可以直接吧那些店铺加到队列中的，其实是一个道理的，就选先加入一个超级源点的话，下一步以要
加入那几个店铺，所以可以直接加入那几个点的

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn=3e3+100;
typedef long long ll;
struct node{
    int x,y;
    ll c;
}a[1001001];
ll dis[maxn][maxn];
int mp[maxn][maxn];
int n,m,k,d;
typedef pair<int, int> PII;
queue<PII>q;
void dfs(){
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    while(!q.empty()){
        auto t=q.front();
        q.pop();
        int x=t.first,y=t.second;
        for(int i=0;i<4;i++){
            int xx=x+dx[i],yy=y+dy[i];
            if(xx<1||xx>n||yy<1||yy>n||mp[xx][yy]){
                continue;
            }
            if(dis[xx][yy]>dis[x][y]+1){
                dis[xx][yy]=dis[x][y]+1;
                q.push({xx,yy});
            }
        }
    }
}
int main(){
    memset(dis,0x3f,sizeof(dis));
    scanf("%d%d%d%d",&n,&m,&k,&d);
    while(m--){
        int x,y;
        scanf("%d%d",&x,&y);
        dis[x][y]=0;
        q.push({x,y});
    }
    for(int i=1;i<=k;i++){
        scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].c);
    }
    while(d--){
        int qq,ww;
        scanf("%d%d",&qq, &ww);
        mp[qq][ww]=1;
    }
    dfs();
    ll ans=0;
    for(int i=1;i<=k;i++){
        ans+=1ll*dis[a[i].x][a[i].y]*a[i].c;
    }
    cout<<ans<<endl;
    return 0;
}

 

 

例题2：173. 矩阵距离

题目链接

视频链接

 

 

 

输入样例：

3 4
0001
0011
0110

输出样例：

3 2 1 0
2 1 0 0
1 0 0 1


题目大意：
就是给你一个只含有0和1的矩阵，问你每一个0距离最近的1的最小距离为多少，如果这个位置上已经是1的就输出0
就是这样
题解：
这个题和上面的题目基本上是一样的就是这个题先把1进行入队，然后在进行BFS

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn=1e3+100;
typedef pair<int, int> PII;
char a[maxn][maxn];
int dis[maxn][maxn];
int n,m;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void bfs(){
    queue<PII>q;
    memset(dis,0x3f,sizeof(dis));
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(a[i][j]=='1'){
                dis[i][j]=0;
                q.push({i,j});
            }
        }
    }
    while(!q.empty()){
        auto t=q.front();
        q.pop();
        int x=t.first,y=t.second;
        for(int i=0;i<4;i++){
            int xx=x+dx[i],yy=y+dy[i];
            if(x<0||x>=n||y<0||y>=m){
                continue;
            }
            if(dis[xx][yy]>dis[x][y]+1){
                dis[xx][yy]=dis[x][y]+1;
                q.push({xx,yy});
            }
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    bfs();
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cout<<dis[i][j]<<" ";
        }
        cout<<"\n";
    }
}