你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的体力值是路径上相邻格子之间高度差绝对值的最大值决定的。

请你返回从左上角走到右下角的最小体力消耗值。

示例 1：

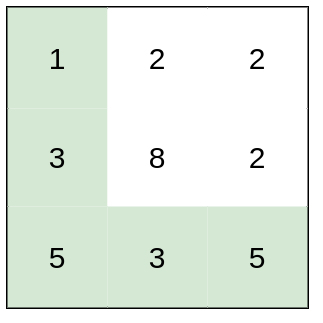
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。
示例 2：

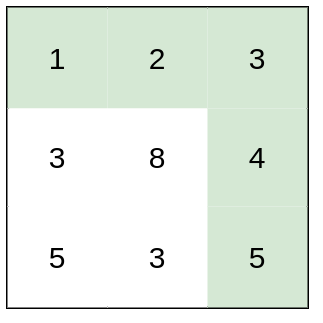
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。
示例 3：

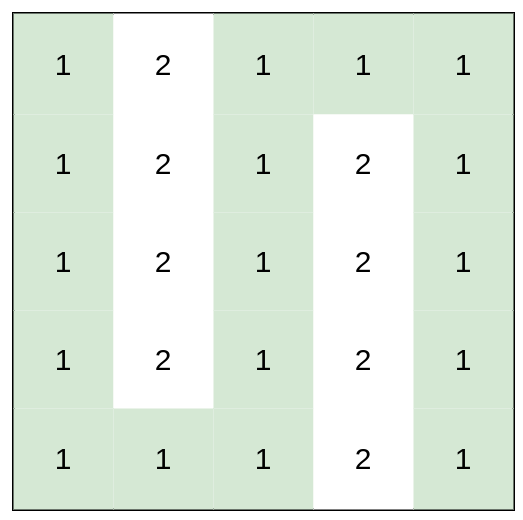
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 1e6

这个题的解法很多，二分dfs,并查集，最短路

1.二分+dfs：

这个题的答案是有单调性的。所以我们可以二分答案

就是对于这个mid，我们从(0,0）进行DFS或者BFS都行，然后判断就是只要走的边的绝对值小于mid，然后判断否能走到(n-1,m-1)这个点

这个复杂度是mnlogC

这里有一个技巧就是他的标记数组开的是一维的就是哈系了一下，就是(x,y)哈希成x*n+m，所以这个（n-1,m-1)就是哈希成了n*m-1

class Solution {
public:
    int dx[4]={0,0,-1,1};
    int dy[4]={-1,1,0,0};
    int minimumEffortPath(vector<vector<int>>& heights) {
        int n=heights.size();
        int m=heights[0].size();
        int l=0,r=1e6,ans;
        while(r>=l){
            int mid=(l+r)/2;
            queue<pair<int,int>> q;
            q.emplace(0,0);
            vector<int> seen(n*m);
            seen[0]=1;
            while(!q.empty()){
                auto [x,y]=q.front();
                q.pop();
                for(int i=0;i<4;i++){
                    int nx=x+dx[i];
                    int ny=y+dy[i];
                    if (nx>=0&&nx<n&&ny>=0&&ny<m&&!seen[nx*m+ny]&&abs(heights[x][y]-heights[nx][ny])<=mid){
                        q.emplace(nx, ny);
                        seen[nx * m + ny] = 1;
                    }
                }
            }
            if(seen[n*m-1]){
                ans=mid;
                r=mid-1;
            }
            else{
                l=mid+1;
            }
        }
        return ans;
    }
};

并查集

我们将这 mnmn 个节点放入并查集中，实时维护它们的连通性。

由于我们需要找到从左上角到右下角的最短路径，因此我们可以将图中的所有边按照权值从小到大进行排序，并依次加入并查集中。当我们加入一条权值为 xx 的边之后，如果左上角和右下角从非连通状态变为连通状态，那么 x 即为答案。

// 并查集模板
class UnionFind {
public:
    vector<int> parent;
    vector<int> size;
    int n;
    // 当前连通分量数目
    int setCount;
    
public:
    UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
        iota(parent.begin(), parent.end(), 0);
    }
    
    int findset(int x) {
        return parent[x] == x ? x : parent[x] = findset(parent[x]);
    }
    
    bool unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            swap(x, y);
        }
        parent[y] = x;
        size[x] += size[y];
        --setCount;
        return true;
    }
    
    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
};

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();
        vector<tuple<int, int, int>> edges;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int id = i * n + j;
                if (i > 0) {
                    edges.emplace_back(id - n, id, abs(heights[i][j] - heights[i - 1][j]));
                }
                if (j > 0) {
                    edges.emplace_back(id - 1, id, abs(heights[i][j] - heights[i][j - 1]));
                }
            }
        }
        sort(edges.begin(), edges.end(), [](const auto& e1, const auto& e2) {
            auto&& [x1, y1, v1] = e1;
            auto&& [x2, y2, v2] = e2;
            return v1 < v2;
        });

        UnionFind uf(m * n);
        int ans = 0;
        for (const auto [x, y, v]: edges) {
            uf.unite(x, y);
            if (uf.connected(0, m * n - 1)) {
                ans = v;
                break;
            }
        }
        return ans;
    }
};

然后还有一个做法就是最短路的做法

class Solution {
private:
    static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();
        
        auto tupleCmp = [](const auto& e1, const auto& e2) {
            auto&& [x1, y1, d1] = e1;
            auto&& [x2, y2, d2] = e2;
            return d1 > d2;
        };
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, decltype(tupleCmp)> q(tupleCmp);
        q.emplace(0, 0, 0);

        vector<int> dist(m * n, INT_MAX);
        dist[0] = 0;
        vector<int> seen(m * n);

        while (!q.empty()) {
            auto [x, y, d] = q.top();
            q.pop();
            int id = x * n + y;
            if (seen[id]) {
                continue;
            }
            if (x == m - 1 && y == n - 1) {
                break;
            }
            seen[id] = 1;
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && max(d, abs(heights[x][y] - heights[nx][ny])) < dist[nx * n + ny]) {
                    dist[nx * n + ny] = max(d, abs(heights[x][y] - heights[nx][ny]));
                    q.emplace(nx, ny, dist[nx * n + ny]);
                }
            }
        }
        
        return dist[m * n - 1];
    }
};

其实我直至都去啊第一种方法，其他的两个我不太会

posted @ 2021-05-31 21:55 lipu123 阅读(97) 评论(0) 收藏举报

刷新页面返回顶部

lipu123

1631. 最小体力消耗路径(二分dfs,并查集，最短路）

并查集

公告