1697. 检查边长度限制的路径是否存在

题目链接

视频链接

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

 

示例 1：

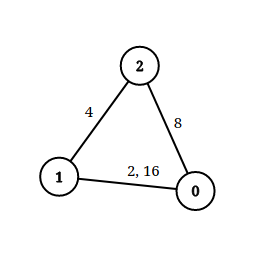
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。
示例 2：

 

 

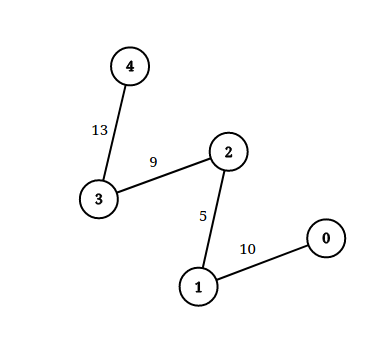
输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。
 

提示：

2 <= n <= 105
1 <= edgeList.length, queries.length <= 105
edgeList[i].length == 3
queries[j].length == 3
0 <= ui, vi, pj, qj <= n - 1
ui != vi
pj != qj
1 <= disi, limitj <= 109
两个点之间可能有 多条 边。
首先注意这个题的询问是离线的，也就是说我们可以先对这个询问对这个每一个询问的limit从小到大拍个序，

然后在对每一个边的长度拍一个序，然后就是我们对于每一次查询的limit我们遍历这个edgeList,把长度在limit[i-1]到

limit[i]之间的边加上就行，这样一来可以极大的降低复杂度，然后就是怎么加边和判断联通性，这个很容易想到用并查集

的，这个好做就好做在这个是离线的

const int maxn = 100010;
struct node{
    int a,b,c,d;
    bool operator< (const node& t) const {
        return c < t.c;
    }
}q[maxn],e[maxn];
class Solution {
public:
    vector<int>p;
    int find(int x){
        if(p[x]!=x){
            p[x]=find(p[x]);
        }
        return p[x];
    }
    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& ee, vector<vector<int>>& qq) {
        int m=ee.size(),k=qq.size();
        for(int i=0;i<m;i++){
            e[i]={ee[i][0],ee[i][1],ee[i][2]};
        }
        for(int i=0;i<k;i++){
            q[i]={qq[i][0],qq[i][1],qq[i][2],i};
        }
        sort(e,e+m);
        sort(q,q+k);
        p.resize(n);
        for(int i=0;i<n;i++){
            p[i]=i;
        }
        vector<bool>ans(k);
        for(int i=0,j=0;i<k;i++){
            while(j<m&&e[j].c<q[i].c){
                int a=e[j].a,b=e[j].b;
                p[find(a)]=find(b);
                j++;
            }
            ans[q[i].d]=find(q[i].a)==find(q[i].b);
        }
        return ans;
    }
};