枚举子集的子集（位运算）

这个操作可以把两层for循环2^(2*n)优化为3^n

讲解链接

题目

给定n个元素，问这n个元素组成的每一个集合的所有子集。(不妨n<=15)

for (int S=1; S<(1<<n); ++S){
    for (int S0=(S-1)&S; S0; S0=(S0-1)&S)
        //do something.
}

这个就是这个操作例如：

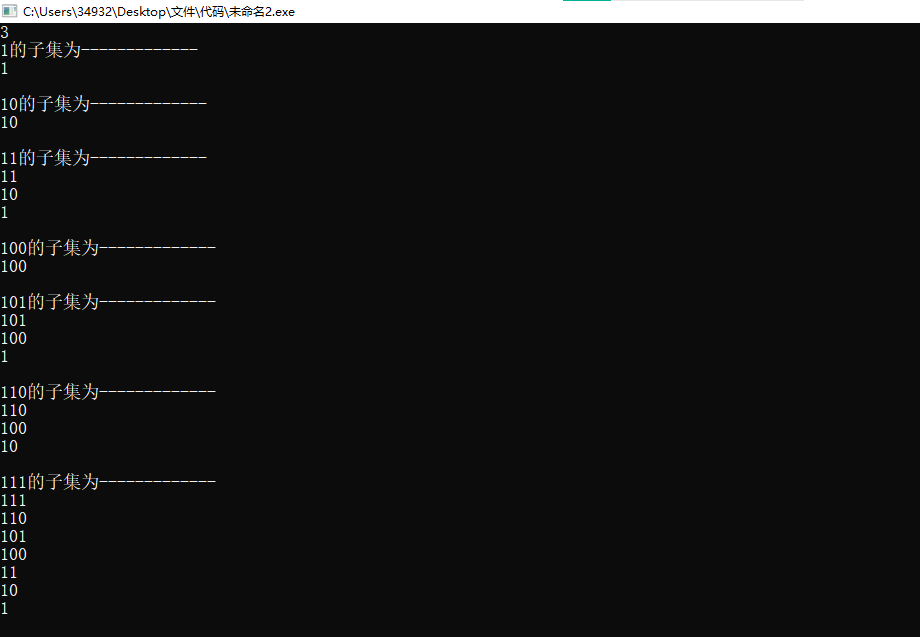
举个例子就是这个就是求3的子集的子集，然后111为3的一个子集，而子集的子集

例如这个题：传送门

视频讲解

class Solution {
public:
    bool canDistribute(vector<int>& nums, vector<int>& quantity) {
        unordered_map<int,int>hash;
        for(auto x:nums) hash[x]++;
        vector<int> w(1);
        for (auto [x, y]: hash) w.push_back(y);//每一个是拥有的个数
        int n=hash.size(),m=quantity.size();
        vector<int>s(1<<m);
        for(int i=0;i<(1<<m);i++){
            for(int j=0;j<m;j++){
                if(i>>j&1){
                    s[i]+=quantity[j];//状态i所需要的j个
                }
            }
        }
        vector<vector<int>> f(n+1,vector<int>(1 << m));
        f[0][0]=1;
        for(int i=0;i<n;i++){
            for(int j=0;j<(1<<m);j++){
                if(f[i][j]){
                    f[i+1][j]=1;
                    for(int t=j^((1<<m)-1),k=t;k;k=(k-1)&t){//这里是求所有0的补集
                        if (s[k] <= w[i + 1]){
                            f[i+1][j|k]=1;
                        }
                    }
                }
            }
        }
        return f[n][(1<<m)-1];
    }
};